Two immiscible liquids of refractive index √2 and 2√2 are filled with equal height h in a vessel. Then apparent depth of bottom surface of the container given that outside medium is air
3√2h4
3h4
3h2
3h4√2
The correct Answer is:A
To solve the problem of finding the apparent depth of the bottom surface of a container filled with two immiscible liquids of different refractive indices, we can follow these steps:
Step 1: Understand the Setup
We have two immiscible liquids with refractive indices:
- Liquid 1: n1=√2
- Liquid 2: n2=2√2
Both liquids are filled to the same height h in the container. The outside medium is air, which has a refractive index of n0=1.
Step 2: Apply the Formula for Apparent Depth
The apparent depth d when looking through a medium can be calculated using the formula:
d=hn
where h is the actual depth and n is the refractive index of the medium.
Step 3: Calculate the Apparent Depth for Each Liquid
1. For Liquid 1 (Refractive Index n1=√2):
- The apparent depth due to this liquid is:
d1=hn1=h√2
2. For Liquid 2 (Refractive Index n2=2√2):
- The apparent depth due to this liquid is:
d2=hn2=h2√2
Step 4: Combine the Apparent Depths
Since both liquids are stacked on top of each other, the total apparent depth d from the top of the first liquid to the bottom of the container is the sum of the apparent depths from both liquids:
d=d1+d2=h√2+h2√2
Step 5: Simplify the Expression
To combine the fractions, we need a common denominator:
d=h√2+h2√2=2h2√2+h2√2=2h+h2√2=3h2√2
Step 6: Final Expression
To express this in a more simplified form, we can multiply and divide by √2:
d=3h2√2⋅√2√2=3√2h4
Conclusion
Thus, the apparent depth of the bottom surface of the container is:
d=3√24h
We have two immiscible liquids with refractive indices:
- Liquid 1: n1=√2
- Liquid 2: n2=2√2
The apparent depth d when looking through a medium can be calculated using the formula:
d=hn
where h is the actual depth and n is the refractive index of the medium.
1. For Liquid 1 (Refractive Index n1=√2):
- The apparent depth due to this liquid is:
d1=hn1=h√2
- The apparent depth due to this liquid is:
d2=hn2=h2√2
Since both liquids are stacked on top of each other, the total apparent depth d from the top of the first liquid to the bottom of the container is the sum of the apparent depths from both liquids:
d=d1+d2=h√2+h2√2
To combine the fractions, we need a common denominator:
d=h√2+h2√2=2h2√2+h2√2=2h+h2√2=3h2√2
To express this in a more simplified form, we can multiply and divide by √2:
d=3h2√2⋅√2√2=3√2h4
Thus, the apparent depth of the bottom surface of the container is:
d=3√24h
Topper's Solved these Questions
Similar Questions
A beaker is filled with two immiscible transparent liquids of refractive indices μ1 and μ2 having thickness of layers d1 and d2 respectively. The apparent depth of the bottom of the beaker is
View SolutionA vessel of depth 2h is half filled with a liquid of refractive index 2√2 and the upper half with another liquid of refractive index √2. The liquids are immiscible. The apparent depth of the inner surface of the bottom of vessel will be:
View SolutionA vessle of depth d is first filled to (23)rd of its depth with a liquid of refractive index 32 and the rest of the vessel is filled with a liquid of refractive index 43. What is the apparent depth of the inner surface of the bottom of the vessle.
View SolutionA vessle of depth d is first filled to (23)rd of its depth with a liquid of refractive index 32 and the rest of the vessel is filled with a liquid of refractive index 43. What is the apparent depth of the inner surface of the bottom of the vessle.
View SolutionEqual volume of two immiscible liquids of densities ρ and 2ρ are filled in a vessel as shown in the figure. Two small holes are punched at depths h/2 and 3h/2 from the surface of lighter liquid. If v1 and v2 are the velocities of efflux at these two holes, then v1/v2 is
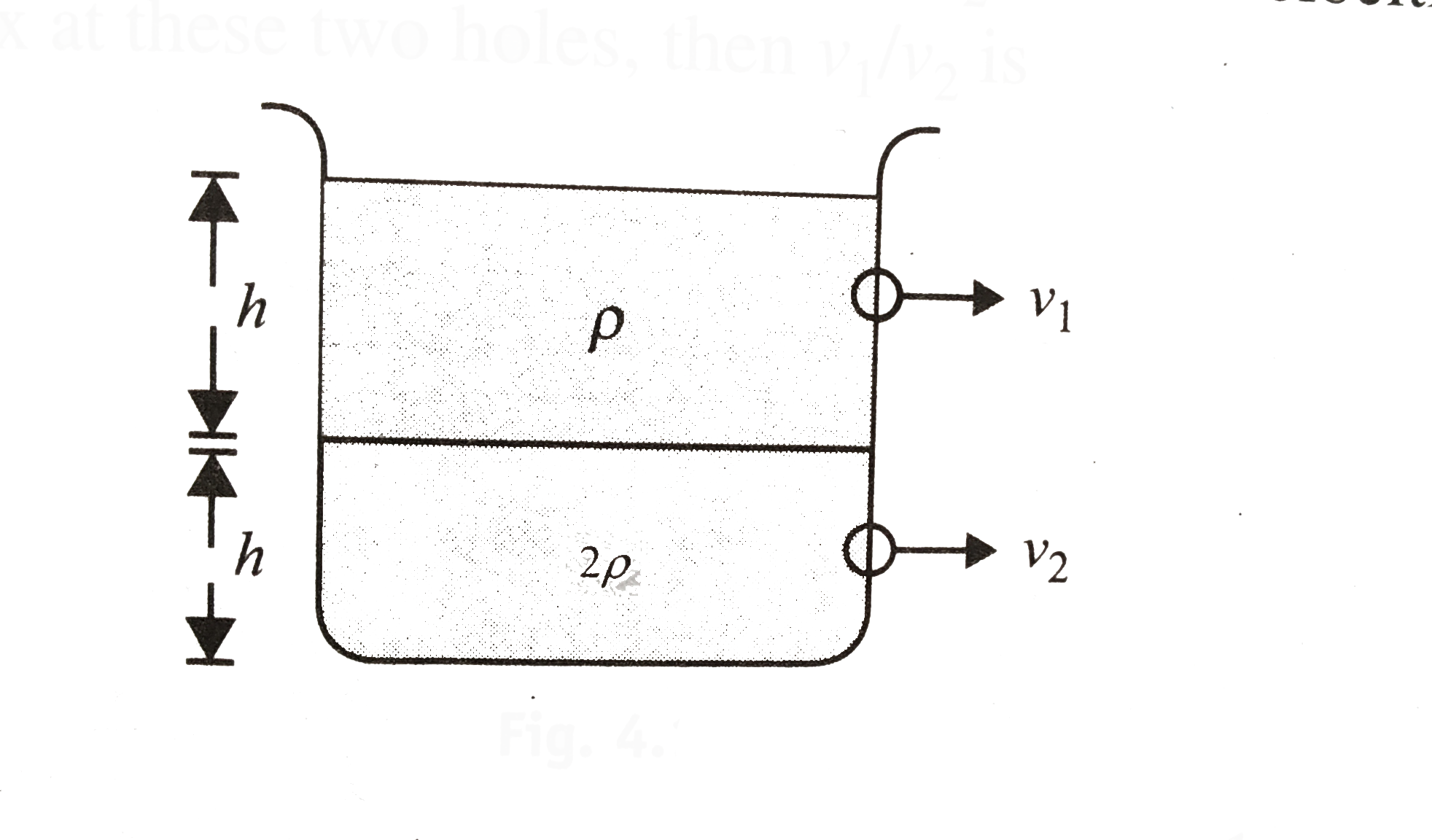
View SolutionEqual volume of two immiscible liquids of densities ρ and 2ρ are filled in a vessel as shown in the figure. Two small holes are punched at depths h/2 and 3h/2 from the surface of lighter liquid. If v1 and v2 are the velocities of efflux at these two holes, then v1/v2 is
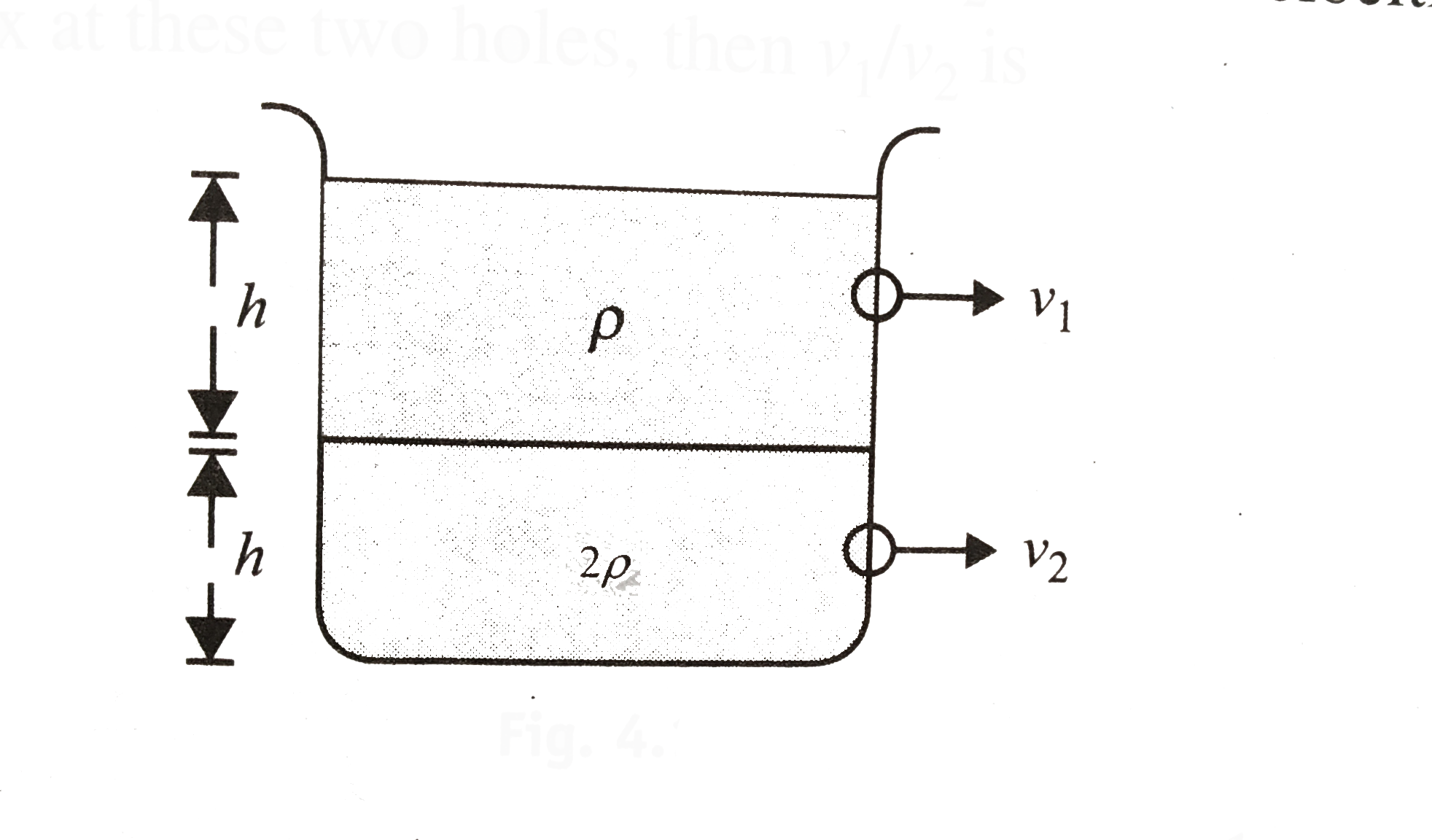
View SolutionEqual volumes of two immiscible liquids of densities ρ and 3ρ are filled in a big vessel. Two small holes are punched at depth h/3 and 4h/3 from upper surface of lighter liquid. If v1 and v2 are velocities of efflux at these two holes, then v1/v2 is

View SolutionA vessel of depth 2d cm is half filled with a liquid of refractive index μ1 and the upper half with a liquid of refractive index μ2. The apparent depth of the vessel seen perpendicularly is
View SolutionEqual volumes of two immiscible liquids of densities ρand2ρ are filled in a vessel as shown in figure. Two small holes are punched at depth h/2 and 3h/2 from the surface of lighter liquid. If v1andv2 are the velocities of efflux at these two holes then (v2v1)2 is

View SolutionA vessel is quarter filled with a liquid of refractive index μ. The remaining parts of the vessel is filled with an immiscible liquid of refractive index 3μ/2. The apparent depth of the vessel is 50% of the actual depth. The value of μ is
View Solution
