A rod of length 1 m is released from rest as shown in the figure below: If ω of rod is √n at the moment it hits the ground, then find n.
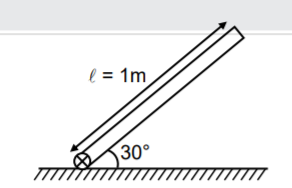
The correct Answer is:15
NA
Topper's Solved these Questions
Similar Questions
A particle mass m is attched to a thin uniform rod of length a at a distance of a4 from the mid-point C as shown in the figure. The mass of the rod is 4m
The moment of inertia of the combined system about an axis passing through O and perpendicular to the rod is
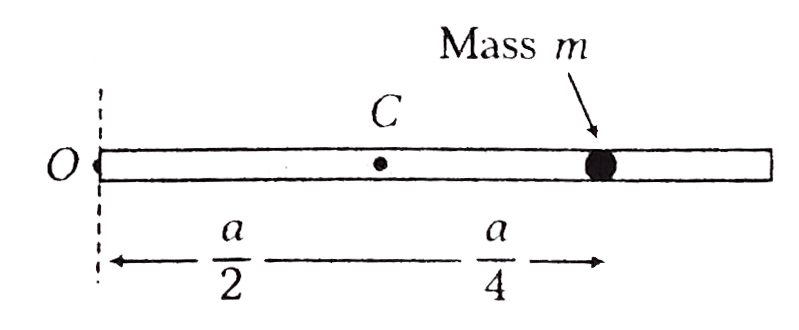
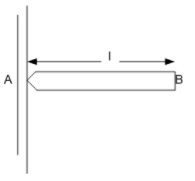
View SolutionA uniform rod AB of length l and mass m is free to rotate about an Axis passing through A and perpendicular to length of the rod. The rod is released from rest as shown in figure. Given that the moment of inertia of the rod about A is ml23 The initial angular acceleration of the rod will be
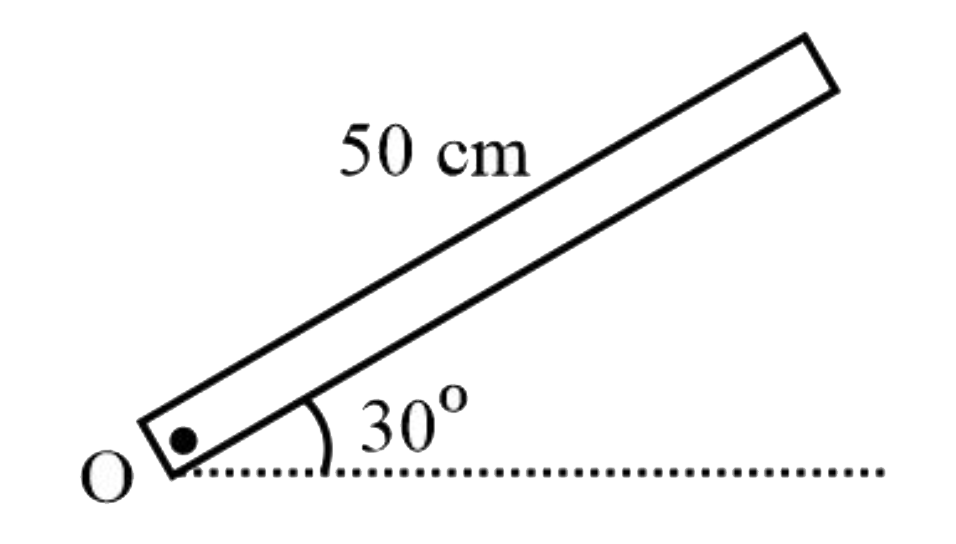
View SolutionA uniform rod of length 50 cm is released in the vertical plane from the position shown in the figure. The rod is hinged smoothly at O. The angular speed of rod when it becomes horizontal is ( take g=10ms−2 )
View SolutionA uniform rod of mass m and length L is suspended with two massless strings as shown in the figure. If the rod is at rest in a horizontal position the ratio of tension in the two strings T1T2 is:

View SolutionA thin rod of length 4l, mass 4 m is bent at the point as shown in the figure. What is the moment of inertia of the rod about the axis passing through O and perpendicular to the plane of the paper?

View Solution
A thin rod of length 4l, mass 4 m is bent at the point as shown in the figure. What is the moment of inertia of the rod about the axis passing through O and perpendicular to the plane of the paper?
View SolutionA thin rod of mass M and length L is released from rest in position shown. The path of centre of mass of rod till the rod become horizontal is [ Assume surface is smooth]
_PHY_208_Q01.png)
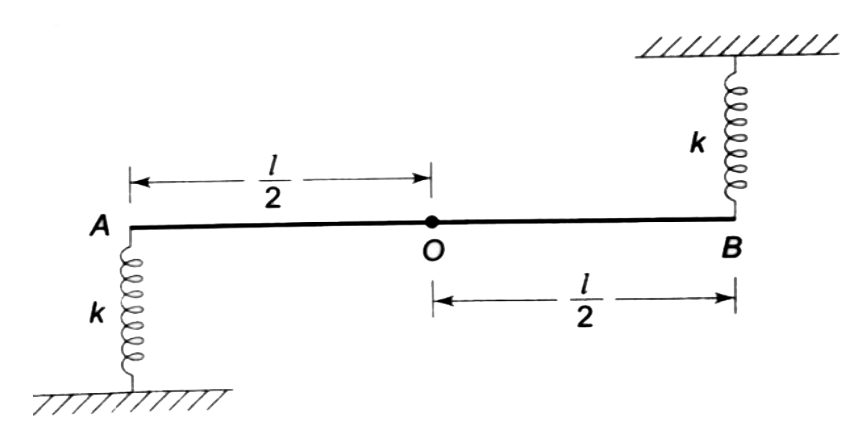
View SolutionThe ends of a rod of length l and mass m are attached to two identical springs as shown in the figure. The rod is free to rotate about its centre O . The rod is depressed slightly at end A and released . The time period of the oscillation is
View SolutionA uniform rod of maass m and length L is placed on the fixed cylindrical surface of radius R at an small angular position θ from the vertical (vertical means line joining centre and vertex of the cylindrical path) as shown in the figure and released from rest. Find the angular velocity ω of the rod at the instant when it crosses the horizontal position (Assume that when rod comes at horizontal position its mid point and vertex of the circular surface coincide). Friction is sufficient to prevent any slipping.

View SolutionA uniform slender rod of mass m and length L is released from rest, with its lower end touching a frictionaless horizontal floor. At the initial moment, the rod is inclined at an angle θ=30∘ with the vertical. Thent he value of normal reaction from the from the floor just after release will be
View Solution
