Moment of inertia of a rigid body is expressed in units of kg . There are two rods A and B made of same metal. Both of them have equal cross-sectional area bur rod A is double in length as compared to rod B. What is the ratio of moment of ineria of rod A to that of rod B?
1
2
4
8
The correct Answer is:A
To find the ratio of the moment of inertia of rod A to that of rod B, we can follow these steps:
Step 1: Understand the Moment of Inertia Formula
The moment of inertia I for a rod about its end is given by the formula:
I=13mL2
where m is the mass of the rod and L is its length.
Step 2: Define the Lengths and Masses of the Rods
Let:
- Length of rod B = L
- Length of rod A = 2L (since rod A is double the length of rod B)
Step 3: Calculate the Mass of Each Rod
Since both rods are made of the same material and have the same cross-sectional area A, their masses can be expressed in terms of their volumes and densities.
The mass m of a rod can be calculated as:
m=Density×Volume
The volume V of a rod is given by:
V=A×L
Thus, we can express the masses as:
- Mass of rod B:
mB=ρ⋅A⋅L
- Mass of rod A:
mA=ρ⋅A⋅(2L)=2ρ⋅A⋅L
Step 4: Substitute Masses into the Moment of Inertia Formula
Now we can substitute the masses into the moment of inertia formula for both rods:
- Moment of inertia of rod A:
IA=13mA(2L)2=13(2ρAL)(4L2)=83ρAL3
- Moment of inertia of rod B:
IB=13mBL2=13(ρAL)(L2)=13ρAL3
Step 5: Find the Ratio of the Moments of Inertia
Now, we can find the ratio of the moment of inertia of rod A to that of rod B:
IAIB=83ρAL313ρAL3
The terms 13, ρ, and AL3 will cancel out, leading to:
IAIB=81=8
Conclusion
The ratio of the moment of inertia of rod A to that of rod B is:
IAIB=8
The moment of inertia I for a rod about its end is given by the formula:
I=13mL2
where m is the mass of the rod and L is its length.
Let:
- Length of rod B = L
- Length of rod A = 2L (since rod A is double the length of rod B)
Since both rods are made of the same material and have the same cross-sectional area A, their masses can be expressed in terms of their volumes and densities.
The mass m of a rod can be calculated as:
m=Density×Volume
The volume V of a rod is given by:
V=A×L
Thus, we can express the masses as:
- Mass of rod B:
mB=ρ⋅A⋅L
- Mass of rod A:
mA=ρ⋅A⋅(2L)=2ρ⋅A⋅L
Now we can substitute the masses into the moment of inertia formula for both rods:
- Moment of inertia of rod A:
IA=13mA(2L)2=13(2ρAL)(4L2)=83ρAL3
- Moment of inertia of rod B:
IB=13mBL2=13(ρAL)(L2)=13ρAL3
Now, we can find the ratio of the moment of inertia of rod A to that of rod B:
IAIB=83ρAL313ρAL3
The terms 13, ρ, and AL3 will cancel out, leading to:
IAIB=81=8
The ratio of the moment of inertia of rod A to that of rod B is:
IAIB=8
Topper's Solved these Questions
- TEST PAPERBOOK - ALLENCHAPTER - TEST PAPEREXERCISE - PHYSICS
4 Videos
- TEST PAPERBOOK - ALLENCHAPTER - TEST PAPEREXERCISE - PHYSICS
4 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Example
1 Videos
- TEST PAPER 1BOOK - ALLENCHAPTER - TEST PAPER 1EXERCISE - PHYSICS
11 Videos
Similar Questions
A metal rod of length 'L' and cross-sectional area 'A' is heated through 'T'∘C What is the force required to prevent the expansion of the rod lengthwise ?
View Solution
Find the moment of inertia of the rod AB about an axis yy as shown in figure. Mass of the rod is m and length is l.
View SolutionA metallic rod of length l and cross-sectional area A is made of a material of Young's modulus Y. If the rod is elongated by an amount y,then the work done is proportional to
View SolutionFour rods of same material and having the same cross section and length have been joined, as shown. The temperature of the junction of four rods will be :
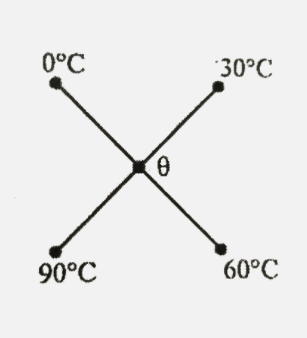
View SolutionThree identical rods, each of mass m and length l, form an equaliteral triangle. Moment of inertia about one of the sides is

View SolutionTwo blocks A and B of masses m and 2m are placed on a smooth horizontal surface. Block B is given a speed of 3m/s. Find
(i) The maximum speed of A
(ii) The minimum speed of B.
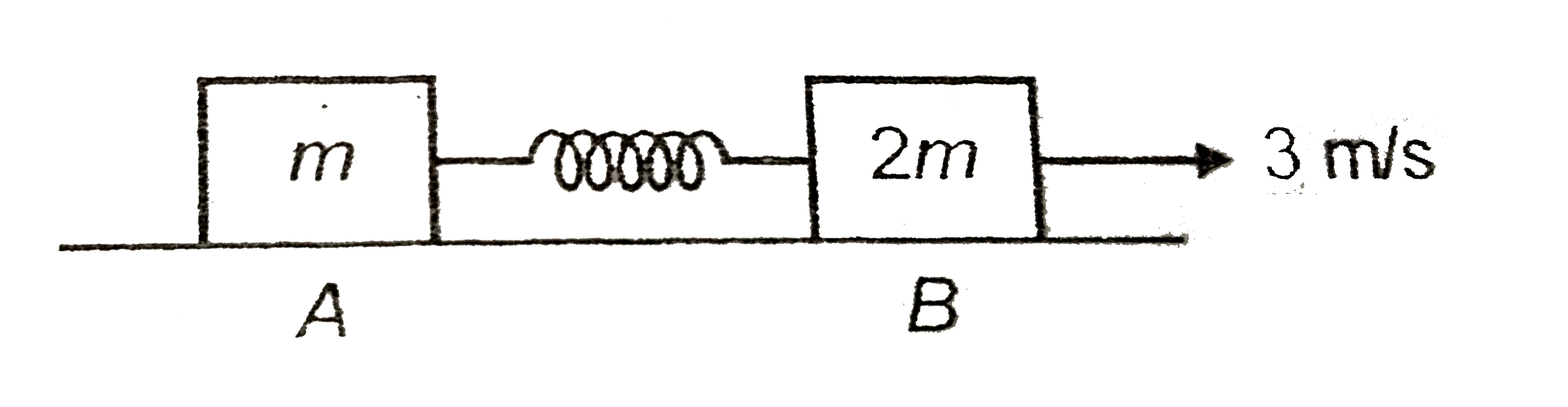
View SolutionThe moment of inertia of a rod about an axis through its centre and perpendicular to it, is 112ML2 (where, M is the mass and L is length of the rod). The rod is bent in the middle, so that two halves make an angle of 45∘. The moment of inertia of the bent rod about the same axis would be
View SolutionThe moment of inertia of a rod about an axis through its centre and perpendicular to it, is 112ML2 (where, M is the mass and L is length of the rod). The rod is bent in the middle, so that two halves make an angle of 60∘. The moment of inertia of the bent rod about the same axis would be
View SolutionIn the diagram shown below all three rods are of equal length L and equal mass M. The system is rotated such that rod B is the axis. What is the moment of inertia of the system ?

View SolutionRatio of energy density of two steel rods is 1:4 when same mass is suspended from the rods. If length of both rods is same then ratio of diameter of rods will be.
View Solution
