A mas m is moving in SHM on a line with amplitude A and frequency f. suddenly half of the mass comes to rest just at the moment when it comes mean position then the new amplitude becomes λA, then λ will be
43832
1√2
√2
1
The correct Answer is:C
To solve the problem step by step, we will analyze the situation involving simple harmonic motion (SHM) and the effects of halving the mass at the mean position.
Step 1: Understand the initial conditions
The mass m is moving in SHM with amplitude A and frequency f. The angular frequency ω1 can be expressed as:
ω1=2πf=√km
where k is the spring constant.
Step 2: Analyze the situation when half the mass comes to rest
When half of the mass comes to rest at the mean position, the effective mass that continues to oscillate is m2. The new angular frequency ω2 for the remaining mass can be calculated as:
ω2=√km2=√2km=√2⋅ω1
Step 3: Apply conservation of momentum
At the mean position, we apply the conservation of momentum. The momentum before half the mass comes to rest is equal to the momentum after:
mv1=m2v2
where v1 is the velocity of the mass m at the mean position, and v2 is the velocity of the mass m2 after half of it comes to rest.
Step 4: Calculate velocities
The velocity v1 at the mean position can be expressed in terms of amplitude and angular frequency:
v1=Aω1
For the remaining mass m2, the new amplitude A2 can be expressed as:
v2=A2ω2
Step 5: Substitute and simplify
Substituting the expressions for v1 and v2 into the momentum equation gives:
m(Aω1)=m2(A2ω2)
Cancelling m from both sides and substituting ω2=√2⋅ω1:
Aω1=12A2(√2⋅ω1)
Cancelling ω1 from both sides (assuming ω1≠0):
A=12A2√2
Step 6: Solve for the new amplitude A2
Rearranging the equation gives:
A2=2A√2=√2A
Step 7: Determine λ
Since it is given that the new amplitude is λA, we can equate:
λA=√2A
Thus, we find:
λ=√2
Final Answer
The value of λ is √2.
---
The mass m is moving in SHM with amplitude A and frequency f. The angular frequency ω1 can be expressed as:
ω1=2πf=√km
where k is the spring constant.
When half of the mass comes to rest at the mean position, the effective mass that continues to oscillate is m2. The new angular frequency ω2 for the remaining mass can be calculated as:
ω2=√km2=√2km=√2⋅ω1
At the mean position, we apply the conservation of momentum. The momentum before half the mass comes to rest is equal to the momentum after:
mv1=m2v2
where v1 is the velocity of the mass m at the mean position, and v2 is the velocity of the mass m2 after half of it comes to rest.
The velocity v1 at the mean position can be expressed in terms of amplitude and angular frequency:
v1=Aω1
For the remaining mass m2, the new amplitude A2 can be expressed as:
v2=A2ω2
Substituting the expressions for v1 and v2 into the momentum equation gives:
m(Aω1)=m2(A2ω2)
Cancelling m from both sides and substituting ω2=√2⋅ω1:
Aω1=12A2(√2⋅ω1)
Cancelling ω1 from both sides (assuming ω1≠0):
A=12A2√2
Rearranging the equation gives:
A2=2A√2=√2A
Since it is given that the new amplitude is λA, we can equate:
λA=√2A
Thus, we find:
λ=√2
The value of λ is √2.
Topper's Solved these Questions
Similar Questions
A block of mass m attached to a massless spring is performing oscillatory motion of amplitude A on a frictionless horizontal plane. If half of the mass of the block off when it is passing through its mean position, the amplitude of oscillation for the remaining system become fA. The value of f is .
View SolutionA particle of mass m performs SHM along a straight line with frequency f and amplitude A:-
View Solution
Knowledge Check
Two particles execute SHM of same amplitude and frequency on parallel lines. They pass one another when moving in opposite directions each time their displacement is one third their amplitude. What is the phase difference between them?
A0B2π3CπDπ6
particle is executing SHM of amplitude A and angular frequency omega.The average acceleration of particle for half the time period is : (Starting from mean position)
View SolutionA block of mass M attached to the free end of a spring of force constant k is nounted on a smooth horizontal table as shown in figure.
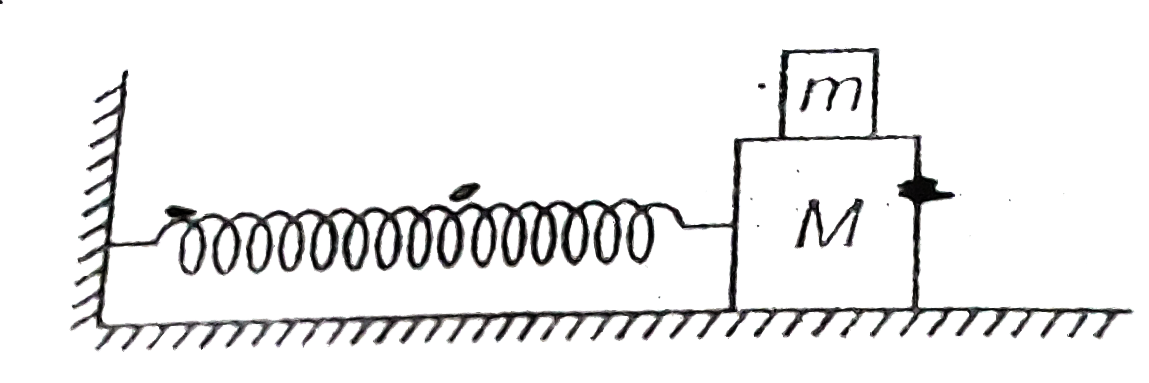
The block executes SHM with amplitude A and frequency f . If an object of mass m is put on it, when the block is passing through its equilibium position and the two move together ,then what is the new amplitude and frequency of vibration?
View SolutionBlock A of mass m is performing SHM of amplitude a. Another block B of mas m is gently placed on A when it passes through mean position and B sticks to A. Find the time period and amplitude of new SHM.
View SolutionA mass m is undergoing SHM in the verticl direction about the mean position y0 with amplitude A and anglular frequency ω. At a distance y form the mean position, the mass detached from the spring. Assume that th spring contracts and does not obstruct the motion of m. Find the distance y. (measured from the mean position). such that height h attained by the block is maximum (Aω2>g).
_E01_175_Q01.png)
View SolutionTwo particles A and B oscillates in SHM having same amplitude and frequencies fA and fB respectively. At t=0 the particle A is at positive extreme position while the particle B is at a distance half of the amplitude on the positive side of the mean position and is moving away from the mean position.
View SolutionA partical excutes SHM with amplitudeA and angular frequency ω. At an instant the particle is at a distance A/5 from the mean position and is moving away from it. Find the time after which it will come back to this position again and also find the time after which it will pass through the mean position.
View SolutionFor any S.H.M., amplitude is 6 cm . If instantaneous potential energy is half the total energy then distance of particle from its mean position is
View Solution
