Question

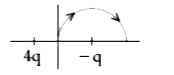
Two charges 4q and -q are kept on x-axis at $(-\frac{d}{2},0)$ and $(\frac{d}{2},0)$ resp. Then charge +q is moved from origin to x=d via semicircular path . Find change in its energy.

Answer

A::C::D

Explanation

To solve the problem, we need to calculate the change in potential energy as the charge +q moves from the origin to the point x = d along a semicircular path in the presence of the two charges, 4q and -q.

1. Identify the positions of the charges:
- Charge 4q is located at \((-d/2, 0)\).
- Charge -q is located at \((d/2, 0)\).
- The charge +q starts at the origin \((0, 0)\) and moves to \((d, 0)\).

2. Calculate the potential energy at the initial position (Point A):
- The potential energy \(U_A\) at the origin due to both charges can be calculated using the formula for electric potential energy:
\( U_A = k \left( \frac{4q \cdot q}{r_1} + \frac{-q \cdot q}{r_2} \right) \)
- Here, \(r_1 = \frac{d}{2}\) (distance from charge 4q) and \(r_2 = \frac{d}{2}\) (distance from charge -q).
- Therefore,
\( U_A = k \left( \frac{4q^2}{d/2} - \frac{q^2}{d/2} \right) = k \left( \frac{4q^2}{d/2} - \frac{q^2}{d/2} \right) = k \left( \frac{4q^2 - q^2}{d/2} \right) = k \left( \frac{3q^2}{d/2} \right) = \frac{6kq^2}{d} \)

3. Calculate the potential energy at the final position (Point B):
- The potential energy \(U_B\) at the point \((d, 0)\) can be calculated similarly:
\( U_B = k \left( \frac{4q \cdot q}{r_1'} + \frac{-q \cdot q}{r_2'} \right) \)
- Here, \(r_1' = \frac{3d}{2}\) (distance from charge 4q) and \(r_2' = \frac{d}{2}\) (distance from charge -q).
- Therefore,
\( U_B = k \left( \frac{4q^2}{3d/2} - \frac{q^2}{d/2} \right) = k \left( \frac{4q^2 \cdot 2}{3d} - \frac{2q^2}{d} \right) = k \left( \frac{8q^2}{3d} - \frac{2q^2}{d} \right) \)
- Simplifying gives:
\( U_B = k \left( \frac{8q^2 - 6q^2}{3d} \right) = \frac{2kq^2}{3d} \)

4. Calculate the change in potential energy:
- The change in potential energy \(\Delta U\) as the charge moves from A to B is given by:
\( \Delta U = U_B - U_A \)
- Substituting the values:
\( \Delta U = \frac{2kq^2}{3d} - \frac{6kq^2}{d} \)
- Finding a common denominator (3d):
\( \Delta U = \frac{2kq^2}{3d} - \frac{18kq^2}{3d} = \frac{2kq^2 - 18kq^2}{3d} = \frac{-16kq^2}{3d} \)

5. Final Result:
- The change in energy as the charge +q moves from the origin to x = d is:
\( \Delta U = -\frac{16kq^2}{3d} \)