A circular disc of mass M and radius R rotating with speed of and another disc of same mass M and radius R/2 placed co axially on first disc, after sometime disc-2 also attain constant speed . Find loss of percentage in energy
The correct Answer is:B
To solve the problem, we need to find the loss of percentage in kinetic energy when two discs are rotating. Here’s a step-by-step breakdown of the solution:
Step 1: Calculate the Moment of Inertia of Each Disc
1. For the first disc (mass M, radius R):
I1=12MR2
2. For the second disc (mass M, radius R/2):
I2=12M(R2)2=12MR24=MR28
Step 2: Calculate the Initial Angular Momentum
- Initially, only the first disc is rotating with angular speed ω and the second disc is at rest (ω2=0):
Li=I1ω+I2⋅0=I1ω=12MR2ω
Step 3: Calculate the Final Angular Momentum
- After some time, both discs rotate with a common angular speed ω2:
Lf=(I1+I2)ω2=(12MR2+MR28)ω2
- Combine the moments of inertia:
Lf=(4MR28+MR28)ω2=5MR28ω2
Step 4: Equate Initial and Final Angular Momentum
- Since no external torque acts on the system:
Li=Lf⟹12MR2ω=5MR28ω2
- Cancel MR2 from both sides:
12ω=58ω2⟹ω2=45ω
Step 5: Calculate Initial Kinetic Energy
- The initial kinetic energy KEi is only from the first disc:
KEi=12I1ω2=12(12MR2)ω2=14MR2ω2
Step 6: Calculate Final Kinetic Energy
- The final kinetic energy KEf is the sum of the kinetic energies of both discs:
KEf=12I1ω22+12I2ω22
- Substitute ω2=45ω:
KEf=12(12MR2)(45ω)2+12(MR28)(45ω)2
- Calculate each term:
KEf=12⋅12MR2⋅1625ω2+12⋅MR28⋅1625ω2
=825MR2ω2+225MR2ω2=1025MR2ω2=25MR2ω2
Step 7: Calculate the Loss in Kinetic Energy
- The loss in kinetic energy ΔKE:
ΔKE=KEi−KEf=14MR2ω2−25MR2ω2
- Find a common denominator (20):
=(520−820)MR2ω2=−320MR2ω2
Step 8: Calculate the Percentage Loss in Kinetic Energy
- Percentage loss:
Percentage Loss=ΔKEKEi×100=−320MR2ω214MR2ω2×100
- Simplifying:
=−32014×100=−3×420×100=−1220×100=−60%
- Since we are interested in the loss:
Loss Percentage=20%
Final Answer
The loss of percentage in energy is 20%.
1. For the first disc (mass M, radius R):
I1=12MR2
I2=12M(R2)2=12MR24=MR28
- Initially, only the first disc is rotating with angular speed ω and the second disc is at rest (ω2=0):
Li=I1ω+I2⋅0=I1ω=12MR2ω
- After some time, both discs rotate with a common angular speed ω2:
Lf=(I1+I2)ω2=(12MR2+MR28)ω2
- Combine the moments of inertia:
Lf=(4MR28+MR28)ω2=5MR28ω2
- Since no external torque acts on the system:
Li=Lf⟹12MR2ω=5MR28ω2
- Cancel MR2 from both sides:
12ω=58ω2⟹ω2=45ω
- The initial kinetic energy KEi is only from the first disc:
KEi=12I1ω2=12(12MR2)ω2=14MR2ω2
- The final kinetic energy KEf is the sum of the kinetic energies of both discs:
KEf=12I1ω22+12I2ω22
- Substitute ω2=45ω:
KEf=12(12MR2)(45ω)2+12(MR28)(45ω)2
- Calculate each term:
KEf=12⋅12MR2⋅1625ω2+12⋅MR28⋅1625ω2
=825MR2ω2+225MR2ω2=1025MR2ω2=25MR2ω2
- The loss in kinetic energy ΔKE:
ΔKE=KEi−KEf=14MR2ω2−25MR2ω2
- Find a common denominator (20):
=(520−820)MR2ω2=−320MR2ω2
- Percentage loss:
Percentage Loss=ΔKEKEi×100=−320MR2ω214MR2ω2×100
- Simplifying:
=−32014×100=−3×420×100=−1220×100=−60%
- Since we are interested in the loss:
Loss Percentage=20%
The loss of percentage in energy is 20%.
Topper's Solved these Questions
Similar Questions
The M.I. of a ring and disc of same mass and radius about their geometric axes will be:
View SolutionA circular disc of mass 2 kg and radius 10 cm rolls without slipping with a speed 2 m/s. The total kinetic energy of disc is
View SolutionA circular disc of mass M and radius R is rotating about its axis with angular speed If about another stationary disc having radius ω1.
R2 and same mass M is dropped co- axially on to the rotating disc. Gradually both discs attain constant angular speed ω2. The energy lost in the process is p% of the initial energy . Value of p is ........
View SolutionA disc of mass M and Radius R is rolling with an angular speed ω on the horizontal plane. The magnitude of angular momentum of the disc about origin is:
View SolutionA disc of mass m and radius R rotating with angular speed ω0 is placed on a rough surface (co-officient of friction =μ). Then

View SolutionA circular disc of mass M1 and radius R, initially moving, With a constant angular speed ω is gently placed coaxially on a stationary circular disc of mass M2 and radius R, as shown in Fig. There is a frictional force between the two discs.
If disc M2 is placed on a smooth surface, then 'determine' the final angular speed of each disc.
b. Determine the work done by friction.
c. Determine the fractional loss in kinetic energy. i.e. △K/Ki
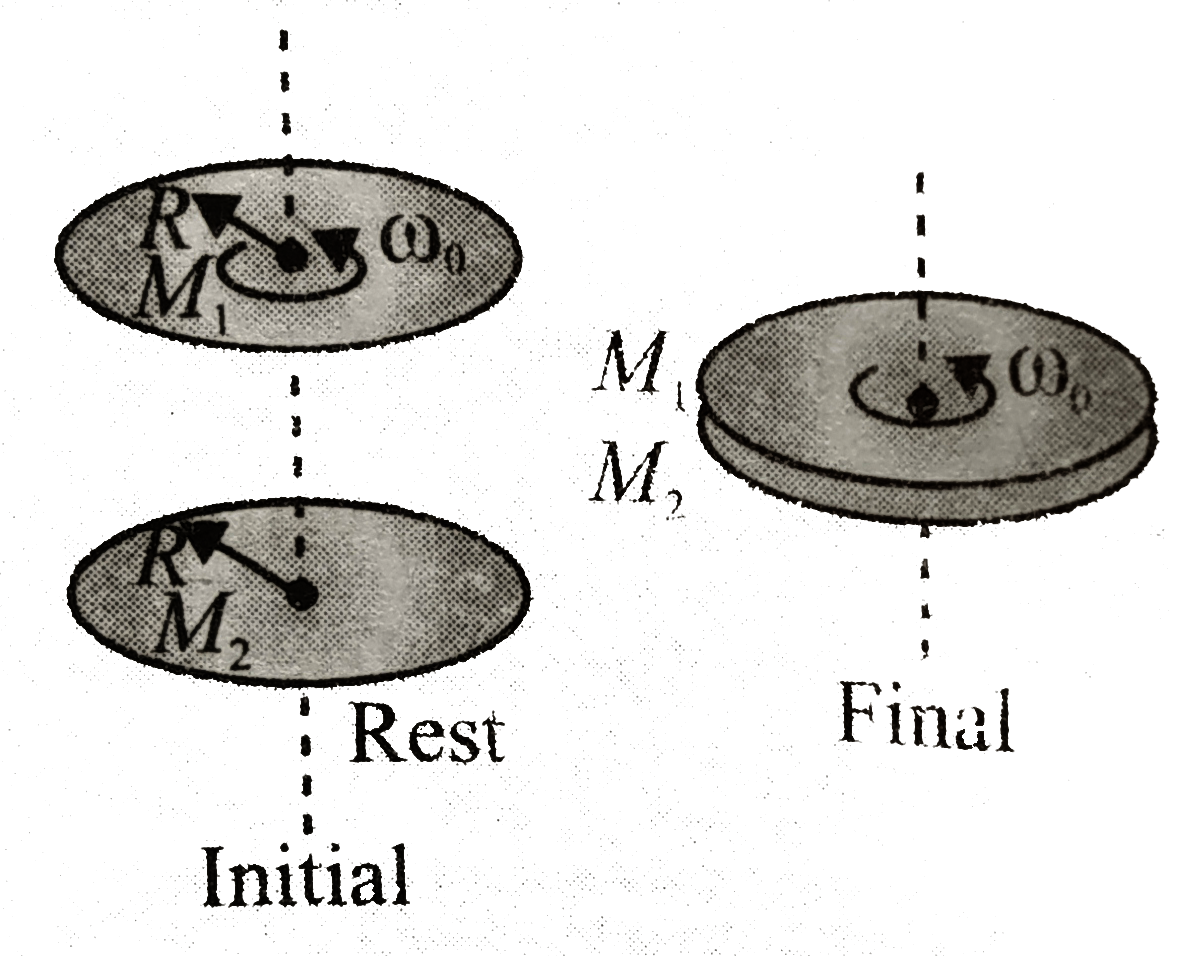
View SolutionA circular disc of mass '2m' and radius '3r' is resting on a flat frictionless surface. Another circular disc of mass m and radius '2r', moving with a velocity 'u'. hits the first disc as shown in the figure. The collision is elastic.
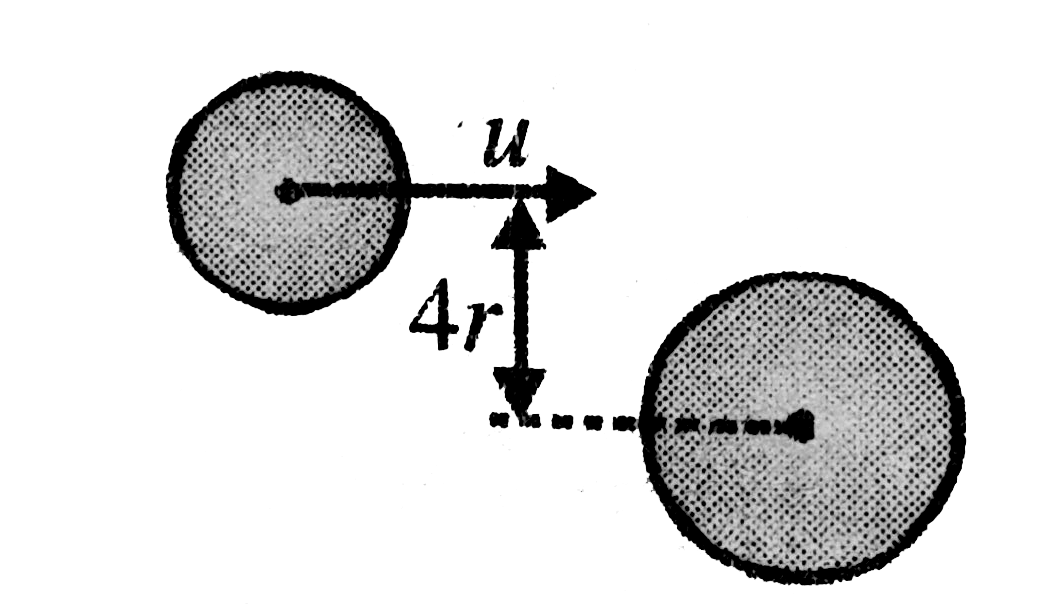
What is the tangential component of final velocity of the smaller disc?
View SolutionA circular disc of mass '2m' and radius '3r' is resting on a flat frictionless surface. Another circular disc of mass m and radius '2r', moving with a velocity 'u'. hits the first disc as shown in the figure. The collision is elastic.
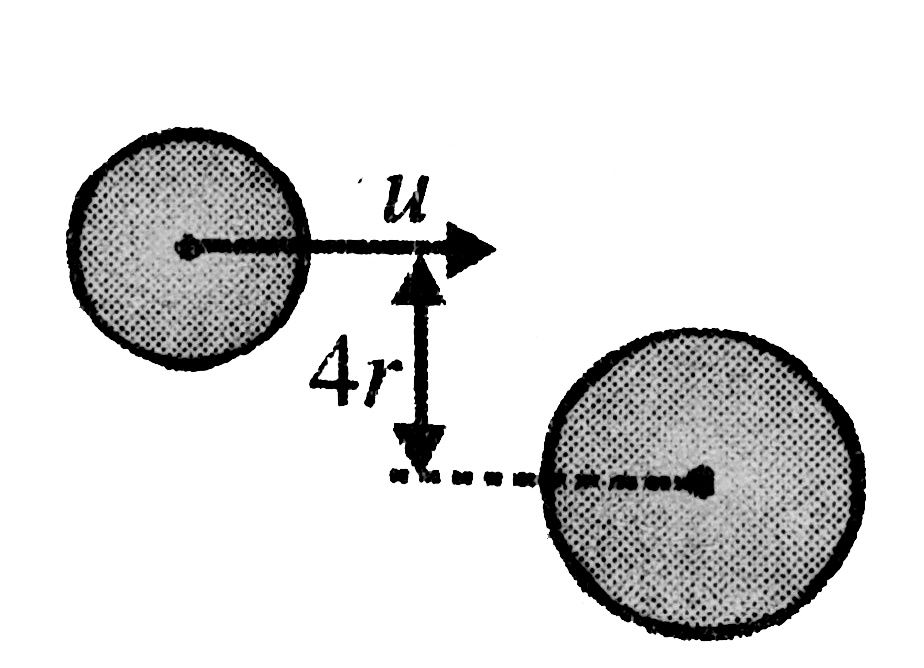 What is the final velocity of the heavier disc?
What is the final velocity of the heavier disc?
View SolutionOut of a disc of mass M and radius R a concentric disc of mass m and radius r is removed. The M.I. of the remaining part about the symmetric axis will be :
View SolutionA circular disc of mass '2m' and radius '3r' is resting on a flat frictionless surface. Another circular disc of mass m and radius '2r', moving with a velocity 'u'. hits the first disc as shown in the figure. The collision is elastic.
What is the magnitude of normal component of final velocity of the smaller disc'?
View Solution
