Two charges q and -q are placedat ( a,0) and (−a,0) on the x-axis. Another charge 2q is taken from ( 0,0) to ( 0,a) , then the work done to do so
q2πε0a
Zero
Infinite
q4πε0a
The correct Answer is:2
To solve the problem of calculating the work done in moving a charge 2q from the origin (0,0) to the point (0,a) in the presence of two charges q and −q located at (a,0) and (−a,0) respectively, we can follow these steps:
Step 1: Determine the Electric Potential at the Points of Interest
The electric potential V due to a point charge Q at a distance r is given by the formula:
V=kQr
where k is Coulomb's constant.
Step 2: Calculate the Potential at the Origin (0,0)
For the charge q at (a,0):
- The distance from (0,0) to (a,0) is a.
- The potential due to charge q at the origin is:
V1=kqa
For the charge −q at (−a,0):
- The distance from (0,0) to (−a,0) is also a.
- The potential due to charge −q at the origin is:
V2=k(−q)a=−kqa
Now, the total potential at the origin VO is:
VO=V1+V2=kqa−kqa=0
Step 3: Calculate the Potential at the Point (0,a)
Now, we calculate the potential at the point (0,a).
For the charge q at (a,0):
- The distance from (0,a) to (a,0) is given by:
r1=√(a−0)2+(0−a)2=√a2+a2=a√2
- The potential due to charge q at (0,a) is:
V′1=kqa√2
For the charge −q at (−a,0):
- The distance from (0,a) to (−a,0) is also:
r2=√(−a−0)2+(0−a)2=√a2+a2=a√2
- The potential due to charge −q at (0,a) is:
V′2=k(−q)a√2=−kqa√2
Now, the total potential at the point (0,a) is:
VP=V′1+V′2=kqa√2−kqa√2=0
Step 4: Calculate the Work Done
The work done W in moving the charge 2q from the origin to the point (0,a) is given by:
W=q(VP−VO)
Substituting the values we found:
W=2q(0−0)=0
Final Answer
The work done in moving the charge 2q from (0,0) to (0,a) is:
0
The electric potential V due to a point charge Q at a distance r is given by the formula:
V=kQr
where k is Coulomb's constant.
For the charge q at (a,0):
- The distance from (0,0) to (a,0) is a.
- The potential due to charge q at the origin is:
V1=kqa
- The distance from (0,0) to (−a,0) is also a.
- The potential due to charge −q at the origin is:
V2=k(−q)a=−kqa
VO=V1+V2=kqa−kqa=0
Now, we calculate the potential at the point (0,a).
- The distance from (0,a) to (a,0) is given by:
r1=√(a−0)2+(0−a)2=√a2+a2=a√2
- The potential due to charge q at (0,a) is:
V′1=kqa√2
- The distance from (0,a) to (−a,0) is also:
r2=√(−a−0)2+(0−a)2=√a2+a2=a√2
- The potential due to charge −q at (0,a) is:
V′2=k(−q)a√2=−kqa√2
VP=V′1+V′2=kqa√2−kqa√2=0
The work done W in moving the charge 2q from the origin to the point (0,a) is given by:
W=q(VP−VO)
Substituting the values we found:
W=2q(0−0)=0
The work done in moving the charge 2q from (0,0) to (0,a) is:
0
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - SECTION-C (OBJECTIVE TYPE QUESTIONS (More than one answer))
13 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - SECTION-D(COMPREHENSION-I)
2 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - SECTION-B (OBJECTIVE TYPE QUESTIONS (ONLY ONE ANSWER) )
1 Video
- ELECTROMAGNETIC WAVESBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - ASSIGNMENT SECTION - D Assertion-Reason Type Questions
25 Videos
- GRAVITATION BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - GRAVITATION EXERCISE - ASSIGNMENT SECTION - D (ASSERTION-REASON TYPE QUESTIONS)
15 Videos
Similar Questions
Two equal positive charges Q are fixed at points (a, 0) and (−a,0) on the x-axis. An opposite charge -q at rest is relased from point (0, a) on the y-axis. The charge -q will
View SolutionTwo equal negative charges −q are fixed at points (0,−a) and (0,a) on y-axis. A poistive charge Q is released from rest at point (2a,0) on the x-axis. The charge Q will
View SolutionTwo point charges +q and -q are held fixed at (−a,0) and (a,0) respectively of a x-y coordinate system then
View SolutionTwo charges 4q and -q are kept on x-axis at (−d2,0) and (d2,0) resp. Then charge +q is moved from origin to x=d via semicircular path . Find change in its energy.
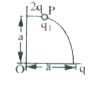
View SolutionTwo point charges q AND 2q are placed at (a,0) and (0,a) A point charge q1 is placed at a P on the quarter circle of radius a as shown in the diagram so that the electric field at the origin becomes zero
View SolutionTwo point charges (Q each are placed at (0,y) and (0-y) A point charge q of the same polarity can move along the x-axis. Then
View SolutionA positive point charge q1 is placed at (a,0) and another positive point charge q2 is placed at (0,a) . Find the force acting on q1.
View SolutionTwo charges q1andq2 are placed at (0,0,d) and (0,0,-d) respectively. Find locus of points where the potential is zero.
View SolutionCharge 2qand−q are placed at (a,0)and(−a,0) as shown in the figure. The coordinates of the point at which electric field intensity is zero will be (x,0) where

View SolutionTwo point charges q each are fixed at (a,0) and (-a,0). A third charge Q is placed at origin. Electrons potential energy of the system will
View Solution
