Consider two uniform discs of the same thickness and different radii R1=R and R2=αR made of the same material. If the ratio of their moments of inertia I1andI2, respectively, about their axes is I1:I2=1:16 then the value of α is :
2
√2
2√2
4
To solve the problem, we need to find the value of α given the ratio of the moments of inertia of two uniform discs with different radii. Let's break it down step by step.
Step 1: Understand the Moment of Inertia for a Disc
The moment of inertia I of a uniform disc about its central axis is given by the formula:
I=12mr2
where m is the mass of the disc and r is its radius.
Step 2: Define the Radii and Moments of Inertia
Let:
- For Disc 1 (radius R1=R):
I1=12m1R2
- For Disc 2 (radius R2=αR):
I2=12m2(αR)2=12m2α2R2
Step 3: Relate the Masses of the Discs
Since both discs are made of the same material and have the same thickness, their masses are proportional to their volumes. The volume V of a disc is given by:
V=πr2h
where h is the thickness. Thus, the mass can be expressed as:
m∝r2
Therefore, we can write:
- m1∝R2
- m2∝(αR)2=α2R2
Step 4: Express the Moments of Inertia in Terms of R
Substituting the mass expressions into the moment of inertia formulas, we have:
I1=12(kR2)R2=12kR4
I2=12(kα2R2)(αR)2=12kα2R4
where k is a constant of proportionality related to the material density and thickness.
Step 5: Set Up the Ratio of Moments of Inertia
We are given that:
I1I2=116
Substituting the expressions for I1 and I2:
12kR412kα2R4=116
The 12kR4 terms cancel out:
1α2=116
Step 6: Solve for α
Taking the reciprocal of both sides gives:
α2=16
Taking the square root of both sides:
α=4
Conclusion
The value of α is:
α=4
The moment of inertia I of a uniform disc about its central axis is given by the formula:
I=12mr2
where m is the mass of the disc and r is its radius.
Let:
- For Disc 1 (radius R1=R):
I1=12m1R2
- For Disc 2 (radius R2=αR):
I2=12m2(αR)2=12m2α2R2
Since both discs are made of the same material and have the same thickness, their masses are proportional to their volumes. The volume V of a disc is given by:
V=πr2h
where h is the thickness. Thus, the mass can be expressed as:
m∝r2
Therefore, we can write:
- m1∝R2
- m2∝(αR)2=α2R2
Substituting the mass expressions into the moment of inertia formulas, we have:
I1=12(kR2)R2=12kR4
I2=12(kα2R2)(αR)2=12kα2R4
where k is a constant of proportionality related to the material density and thickness.
We are given that:
I1I2=116
Substituting the expressions for I1 and I2:
12kR412kα2R4=116
The 12kR4 terms cancel out:
1α2=116
Taking the reciprocal of both sides gives:
α2=16
Taking the square root of both sides:
α=4
The value of α is:
α=4
Topper's Solved these Questions
Similar Questions
Two disc made of same material and same thickness having radius R and μR.Their moment of inertia about their own axis are in ratio 1:16. Calculate the value of μ
View SolutionTwo discs have same mass and thickness. Their materials are of densities ρ1 and ρ2. The ratio of their moment of inertia about central axis will be
View Solution
Knowledge Check
Two particles of equal masses are revolving in circular paths of radii, r1andr2 respectively with the same period . The ratio of their centripetal force is -
Ar1/r2B√r2/r1C(r1/r2)2D(r2/r1)2
Two discs have same mass and thickness. Their materials are of densities π1 and π2. The ratio of their moment of inertia about central axis will be
View SolutionIn the given circuit, if I1andI2 be the current in resistances R1andR2, respectively, then
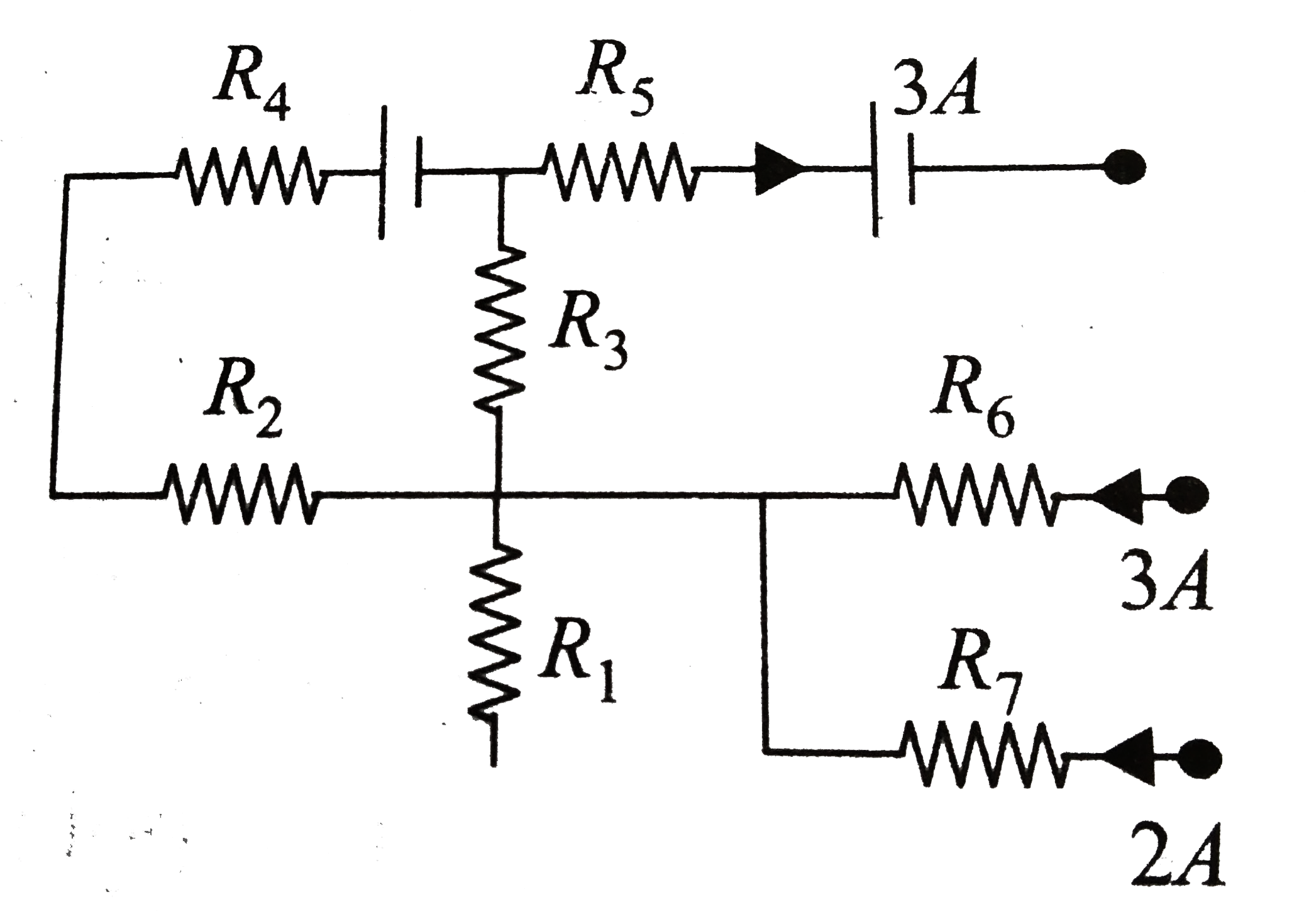 .
.
View SolutionThree plates A, B and C are placed close to each other with +Q charge given to the middle plate. The inner surfaces to A and C can be connected to earth through plate D and keys K1 and K2 . The plates D is a dielectric slab with dielectric constant K1 then the charge that will flow through plate D and keys K1 and K2 . The plate D is a dielectric slab with dielectric constant K, then the charge that will flow though plate D when K2 is closed and K2 is open is

View SolutionTwo rings of radius R and nR made of same material have the ratio of moment of inertia about an axis passing through center is 1:8. The value of n is
View SolutionTwo solid spheres are made up of the same material of density ρ. The ratio of their radii is 1:2. The ratio of their moments of inertia about their respective diameters is
View SolutionThe masses of two uniform discs are in the ratio 2:1 and their radii are in the ratio 1:2. The ratio of their moments of inertia about the axis passing through their respective centres normal to plane is
View SolutionTwo discs have same mass and thickness. Their materials are of densities d1andd2. The ratio of their moments of inertia about an axis passing through the centre and perpendicular to the plane is
View Solution
