Match the thermodynamic processes taking place in a system with the correct conditions. In the table : ΔQ is the heat supplied, ΔW is the work done and ΔU is change in internal energy of the system .
ProcessCondition(I)Adiabatic(A)ΔW=0(II)Isothermal(B)ΔQ=0(III)Isochoric(C)ΔU≠0 , ΔU≠0 , ΔQ≠0(IV)Isobaric(D)ΔU=0
(I) - (B), (II) - (A), (III) - (D), (IV) - (C )
(I) - (B), (II) - (D), (III) - (A), (IV) - (C )
(I) - (A), (II)- (A), (III) - (B), (IV) - (C )
(I) - (A), (II) - (B), (III) - (D), (IV) - (D)
To solve the problem of matching the thermodynamic processes with their corresponding conditions, we need to analyze each process and the given conditions.
Step 1: Understand the Processes
1. Adiabatic Process: In this process, there is no heat exchange with the surroundings. Therefore, the heat supplied (ΔQ) is zero.
2. Isothermal Process: In this process, the temperature remains constant. The internal energy change (ΔU) is zero because internal energy is a function of temperature.
3. Isochoric Process: In this process, the volume remains constant. Hence, the work done (ΔW) is zero, and there can be a change in internal energy (ΔU) due to heat exchange.
4. Isobaric Process: In this process, the pressure remains constant. There can be heat exchange (ΔQ) and a change in internal energy (ΔU).
Step 2: Analyze the Conditions
- Condition A: ΔW = 0
- Condition B: ΔQ = 0
- Condition C: ΔU ≠ 0
- Condition D: ΔU = 0
Step 3: Match Processes with Conditions
1. Adiabatic Process (I): Since there is no heat exchange, it matches with Condition B (ΔQ = 0).
2. Isothermal Process (II): Since the internal energy change is zero, it matches with Condition D (ΔU = 0).
3. Isochoric Process (III): Since the work done is zero and there can be a change in internal energy, it matches with Condition A (ΔW = 0).
4. Isobaric Process (IV): Since there can be heat exchange and a change in internal energy, it matches with Condition C (ΔU ≠ 0).
Final Matching
- I (Adiabatic) - B (ΔQ = 0)
- II (Isothermal) - D (ΔU = 0)
- III (Isochoric) - A (ΔW = 0)
- IV (Isobaric) - C (ΔU ≠ 0)
Summary of Matches
- I - B
- II - D
- III - A
- IV - C
1. Adiabatic Process: In this process, there is no heat exchange with the surroundings. Therefore, the heat supplied (ΔQ) is zero.
2. Isothermal Process: In this process, the temperature remains constant. The internal energy change (ΔU) is zero because internal energy is a function of temperature.
3. Isochoric Process: In this process, the volume remains constant. Hence, the work done (ΔW) is zero, and there can be a change in internal energy (ΔU) due to heat exchange.
4. Isobaric Process: In this process, the pressure remains constant. There can be heat exchange (ΔQ) and a change in internal energy (ΔU).
- Condition A: ΔW = 0
- Condition B: ΔQ = 0
- Condition C: ΔU ≠ 0
- Condition D: ΔU = 0
1. Adiabatic Process (I): Since there is no heat exchange, it matches with Condition B (ΔQ = 0).
2. Isothermal Process (II): Since the internal energy change is zero, it matches with Condition D (ΔU = 0).
3. Isochoric Process (III): Since the work done is zero and there can be a change in internal energy, it matches with Condition A (ΔW = 0).
4. Isobaric Process (IV): Since there can be heat exchange and a change in internal energy, it matches with Condition C (ΔU ≠ 0).
- I (Adiabatic) - B (ΔQ = 0)
- II (Isothermal) - D (ΔU = 0)
- III (Isochoric) - A (ΔW = 0)
- IV (Isobaric) - C (ΔU ≠ 0)
- I - B
- II - D
- III - A
- IV - C
Topper's Solved these Questions
Similar Questions
Match the column :-
Column - IColumn - IIAAdiabatic processPq=0BIsothermal processQΔH=0CIsoenthalpic processRΔT=0DIsoentropic processSΔS=0
View Solution50 J heat is supplied to a gaseous system, simultaneously the gas expands against external pressure 2 atm by 0.8 L. The change in internal energy of the system will be
View SolutionA gas at a pressure of 1 atm is compressed at a constant pressure from 10.0 litres to 2.0 litres. If 500 J of heat energy leaves the gas calculate (i) the work done by the gas and (ii) the change in its internal energy.
View SolutionRefer to figure. Let ΔU1 and ΔU2 be the changes in internal energy in the system in process A+B and ΔW be the net work done by the system in the process A+B,

View Solution500cm3 of a sample of an ideal gas is compressed by an average pressure of 0.1atm of 250cm3. During this process, 10J of heat flows out to the surroundings. Calculate the change in internal enegry of the system.
View Solution500cm3 of a sample of an ideal gas is compressed by an average pressure of 0.1atm of 250cm3. During this process, 10J of heat flows out to the surroundings. Calculate the change in internal enegry of the system.
View SolutionIn the diagram, the graph between volume and pressure for a thermodynamical process in shown. If UA=0,UB=20J and the energy given from B to C is 30J, then at the stage of C, the internal energy of the system is –
View Solution0.5 moles of an ideal monoatomic gas undergoes a thermodynamic process from A to B as shown in figure. The change in internal energy of the gas during the process from A to B is
View SolutionIf ΔU and ΔW represent the increase in internal energy and work done by the system resectively in a thermodynamical process, which of the following is true?
View SolutionThermodynamic processes are indicated in the following diagrams
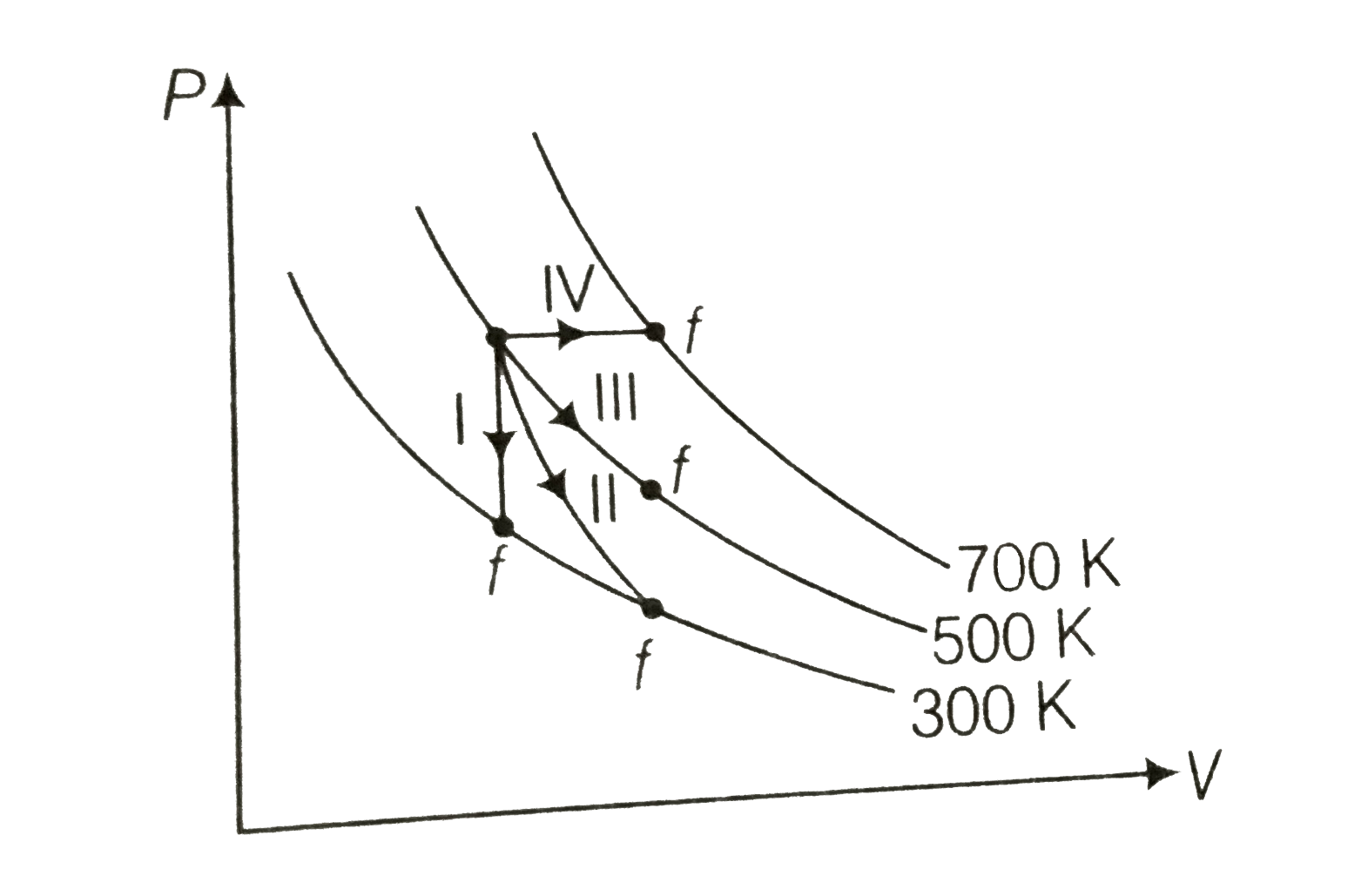
Match the following
Column - IColumn -IIPProcess IaAdiabaticQProcess IIbIsobaricRProcess IIIcIsochoricSProcess IVdIsothermal
View Solution
