An insect is at the bottom of a hemispherical ditch of radius 1 m. It crawls up the ditch but starts slipping after it is at height h from the bottom . If the coefficient of friction between the ground and the insect is 0.75 , then h is : (g=10ms−2)
0.20 m
0.45 m
0.60 m
0.80 m
To solve the problem step by step, we will analyze the forces acting on the insect as it crawls up the hemispherical ditch and determine the height h at which it starts slipping.
Step 1: Understand the setup
The insect is at the bottom of a hemispherical ditch with a radius R=1m. As it crawls up, it reaches a height h from the bottom where it begins to slip due to insufficient friction.
Step 2: Draw the free body diagram
At height h, the insect experiences:
- Its weight mg acting downwards.
- A normal force N acting perpendicular to the surface of the ditch.
- A frictional force f acting tangentially along the surface of the ditch.
Step 3: Resolve the weight into components
At height h, the angle θ can be determined using the relationship:
cosθ=R−hR
where R=1m. The components of the weight are:
- Perpendicular to the surface: mgcosθ
- Tangential to the surface: mgsinθ
Step 4: Apply the conditions for equilibrium
In the vertical direction, the normal force balances the perpendicular component of the weight:
N=mgcosθ
In the horizontal direction, the frictional force is given by:
f=μN
where μ=0.75. Therefore,
f=0.75⋅mgcosθ
Step 5: Set up the equation for slipping
The insect starts slipping when the frictional force equals the tangential component of the weight:
0.75⋅mgcosθ=mgsinθ
Step 6: Simplify the equation
Dividing both sides by mg (assuming m≠0):
0.75cosθ=sinθ
Rearranging gives:
tanθ=0.75
Step 7: Determine θ
Using the tangent value:
tanθ=34
This corresponds to a right triangle where the opposite side is 3 and the adjacent side is 4. Therefore, using the Pythagorean theorem:
Hypotenuse=√32+42=5
Step 8: Calculate the height h
Using the cosine relation:
cosθ=45
At height h:
cosθ=R−hR⟹45=1−h1
Solving for h:
1−h=45⟹h=1−45=15=0.2m
Final Answer
Thus, the height h at which the insect starts slipping is:
0.2m
The insect is at the bottom of a hemispherical ditch with a radius R=1m. As it crawls up, it reaches a height h from the bottom where it begins to slip due to insufficient friction.
At height h, the insect experiences:
- Its weight mg acting downwards.
- A normal force N acting perpendicular to the surface of the ditch.
- A frictional force f acting tangentially along the surface of the ditch.
At height h, the angle θ can be determined using the relationship:
cosθ=R−hR
where R=1m. The components of the weight are:
- Perpendicular to the surface: mgcosθ
- Tangential to the surface: mgsinθ
In the vertical direction, the normal force balances the perpendicular component of the weight:
N=mgcosθ
f=μN
where μ=0.75. Therefore,
f=0.75⋅mgcosθ
The insect starts slipping when the frictional force equals the tangential component of the weight:
0.75⋅mgcosθ=mgsinθ
Dividing both sides by mg (assuming m≠0):
0.75cosθ=sinθ
Rearranging gives:
tanθ=0.75
Using the tangent value:
tanθ=34
This corresponds to a right triangle where the opposite side is 3 and the adjacent side is 4. Therefore, using the Pythagorean theorem:
Hypotenuse=√32+42=5
Using the cosine relation:
cosθ=45
At height h:
cosθ=R−hR⟹45=1−h1
Solving for h:
1−h=45⟹h=1−45=15=0.2m
Thus, the height h at which the insect starts slipping is:
0.2m
Topper's Solved these Questions
Similar Questions
A block of mass 2kg lying on ice when given a velocity of 6ms−1 is stopped by friction in 5s. The coefficient of friction between the block and ice is (g=10 ms−2)
View SolutionFing the maximum speed with which an automobile can round a curve of radius 8 m without slipping of the road is unbanked and he coefficient of friction between the orad an the tyres is 0.8(g=10m/2)
View Solution
Knowledge Check
A ball is dropped from a height h on the ground If the coefficient of restitution is e, the height to which the ball goes up after it rebounds for the nth time is
Ahe2nBhenCe2nhDhe2nThe mass of a bicycle rider along with the bicycle is 100 kg. he wants to cross over a circular turn of radius 100 m with a speed of 10ms−1. If the coefficient of friction between the tyres and the road is 0.6, will the rider be able to cross the turn? Take g=10ms−2.
A300NB600NC1200ND150N
A body of mass m falls from height h, on the ground, If e is the coefficient of restitution between body and the ground, then the height upto which it rises after ten collisions is
View SolutionA car starts from rest at time t = 0 and it a-t graph is shown in figure. A coin is initially at rest on the floor of the car. At t = 1 s the coin begins to slip and it stops slipping at t = 3 s. The coefficient of static friction between the floor and the coin is (g = 10 m/s2)
_PHY_E05_188_Q02.png)
View SolutionA house is built on the top of a hill with 45∘slope Due to the sliding of meterial and sand top from top to the bottom of till , the slip angle has been redaced if the coefficient of static friction between sand particles is 0.75 what is the final angle attated by bill ? (tan−10.75=37∘)

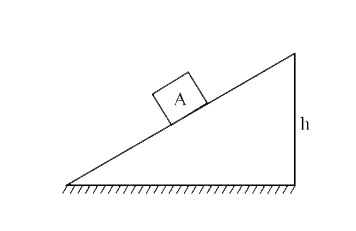
View SolutionA rough wedge of slant length 5 m is kept as shown in the figure. Find the height h if the block of weight 10N just starts to slip in the given figure. The coefficient of friction between the block & the wedge is . 1√3
View SolutionA ball is dropped from height 5m. The time after which ball stops rebounding if coefficient of restitution between ball and ground e=1/2, is
View SolutionA small ball of mass m=1 g is placed at the bottom of a watch glass of radius R=1 m. It is displaced by h=1 cm along the glass surface and released. Calculate the total distance deseribed by it before it comes to rest at the bottom, if μ=0.1 is the coefficient of friction between the ball and the watch glass.
View Solution
