An insect crawls up a hemispherical surface very slowly (see the figure). The coefficient of friction between the insect and the surface is 1/3. If the line joining the centre of the hemispherical surface to the insect makes an angle α with the vertical, the maximum possible value of α is given by
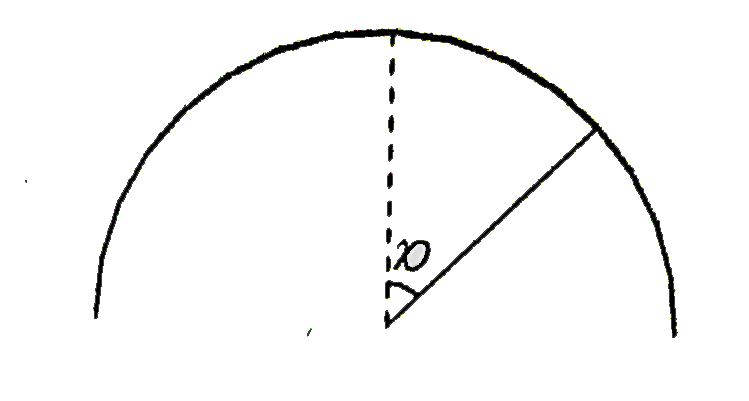
cotα=3
tanα=3
secaplha=3
cosecα=3
Step by step video & image solution for An insect crawls up a hemispherical surface very slowly (see the figure). The coefficient of friction between the insect and the surface is 1/3. If the line joining the centre of the hemispherical surface to the insect makes an angle alpha with the vertical, the maximum possible value of alpha is given by by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
Similar Questions
If the coefficient of friction between an insect and bowl is μ and the radius of the bowl is r, find the maximum height to which the insect can crawl in the bowl.
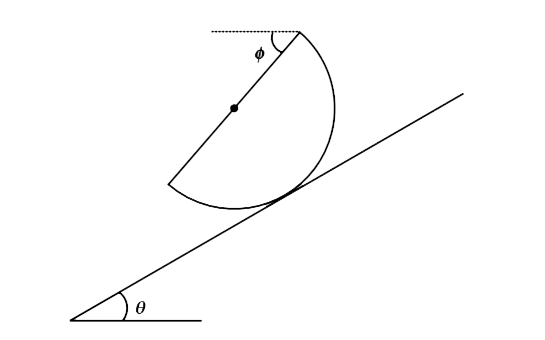
View SolutionA uniform hemisphere placed on an incline is on verge of sliding. The coefficient of friction between the hemisphere and the incline is μ=0.3.
Find the angle ϕ that the circular base of the hemisphere makes with the horizontal.
Given sin(tan−10.3)≅0.29 and sin−1(0.77)≅50∘
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
An insect craws up a hemispherical surface very slowly (see fig.). The coefficient of friction between the insect and the surface is 1/3. If the line joining the center of the hemispherical surface to the insect makes an angle α with the vertical, the maximum possible value of α is given by
 Acotα=3Btanα=3Csecα=3Dcosecα=3
Acotα=3Btanα=3Csecα=3Dcosecα=3 - Question 2 - Select One
The coefficient of friction between an insect and a hemispherical bowl of radius r is μ. The maximum height to which the insect can crawl in the bowl is
Ar√1+μ2Br[1−1√1+μ2]Cr√1+μ2Dr[√1+μ2−1] - Question 3 - Select One
A force of 100N is applied on a block of mass 3kg as shown in the figure. The coefficient of friction between the surface and the block is μ=1√3 . The friction force acting on the bock is.
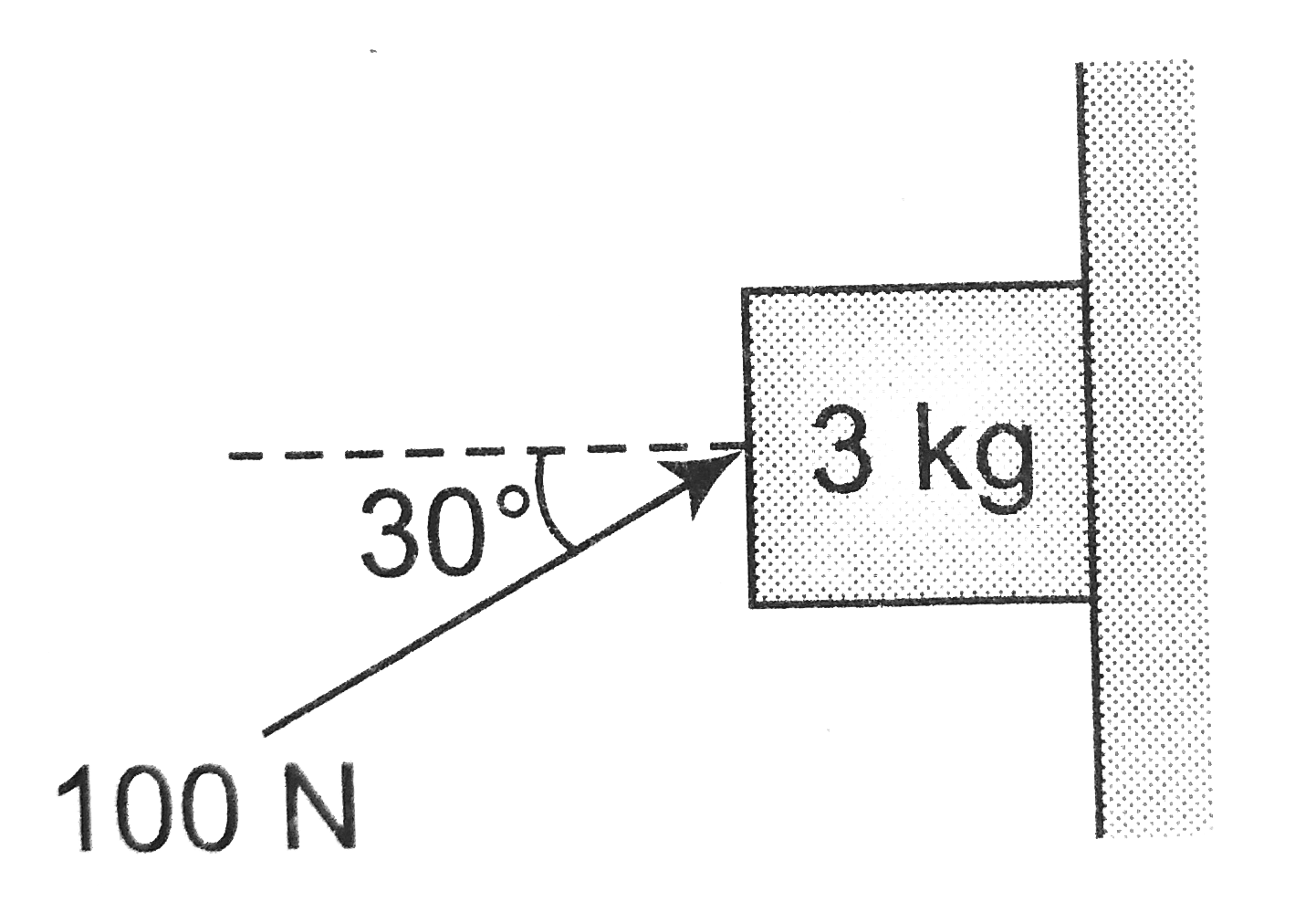 A15N downwardB25N upwardC20N downwordD30N upward
A15N downwardB25N upwardC20N downwordD30N upward
The coefficient of friction between a hemispherical bowl and an insect is √0.44 and the radius of the bowl is 0.6m. The maximum height to which an insect can crawl in the bowl will be
View SolutionThe coefficient of friction between a hemispherical bowl and an insect is √0.44 and the radius of the bowl is 0.6m. The maximum height to which an insect can crawl in the bowl will be .
View Solution
An insect of mass m, starts moving on a rough inclined surface from point A. As the surface is vert sticky, the corfficient of fricion between the insect and the incline is μ=1. Assume that it can move in any direction, up the incline or down the incline thenView SolutionA particle is placed at rest inside a hollow hemisphere of radius R. The coefficient of friction between the particle and the hemisphere is μ=1√3. The maximum height up to which the particle can remain stationary is
View SolutionIn the situration shown in the figure the friction coefficient between M and the horizontal surface is μ. The force F is applied at an angle θ with vertical. The correct statements are
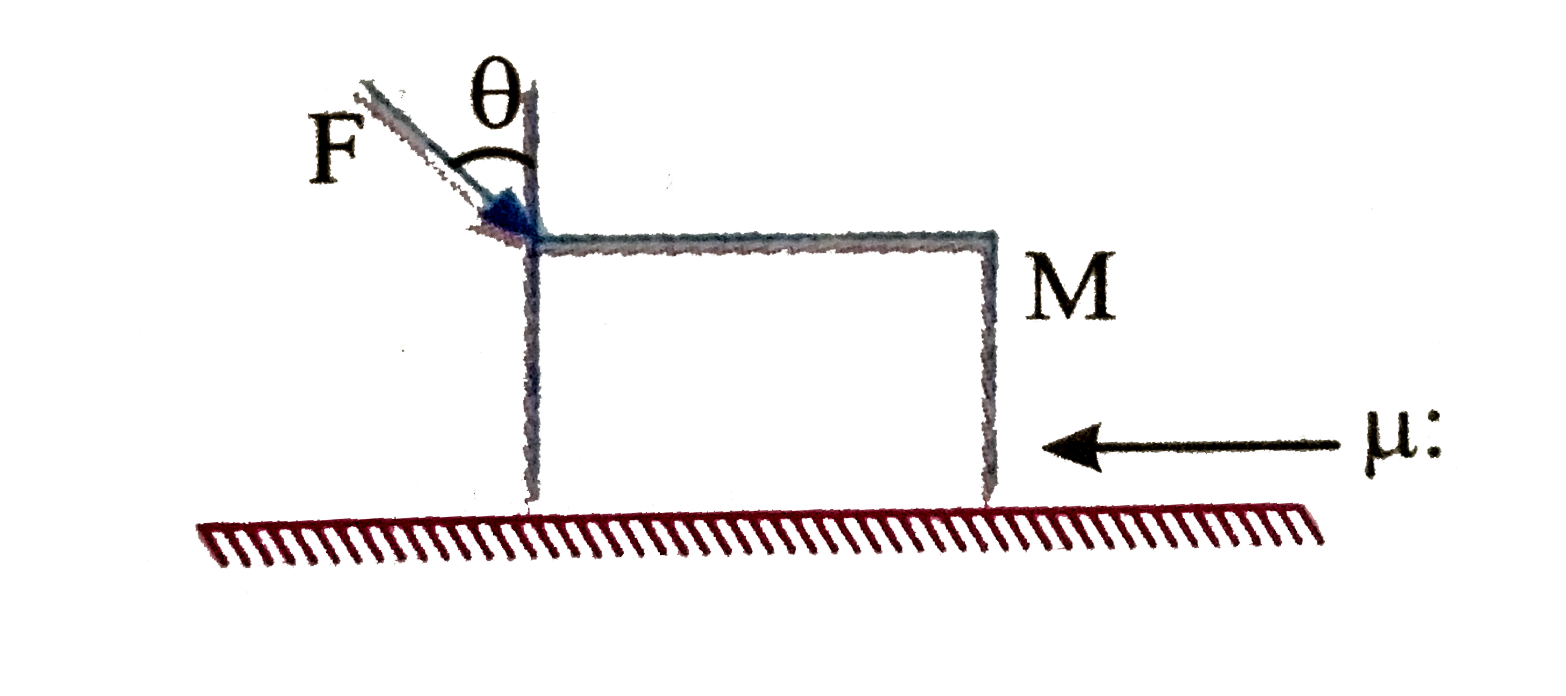 View Solution
View Solution

