A block A of mass m1 rests on a horizontal table. A light string connected to it passes over a frictionless pulley at the edge of table and from its other end another block B of mass m2 is suspended. The coefficient of knetic friction between the block and table is μk . When the block A is sliding on the table, the tension in the string is.
(m2−μkm1)gm1+m2
m1m2(1+μk)gm1+m2
m1m2(1−μk)gm1+m2
(m2+μkm1)gm1+m2
Step by step video & image solution for A block A of mass m_(1) rests on a horizontal table. A light string connected to it passes over a frictionless pulley at the edge of table and from its other end another block B of mass m_(2) is suspended. The coefficient of knetic friction between the block and table is mu_(k) . When the block A is sliding on the table, the tension in the string is. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
If coeffiecient of friction between the block of mass 2kg and table is 0.4 then out acceleration of the system and tension in the string. (g=10m/s2)
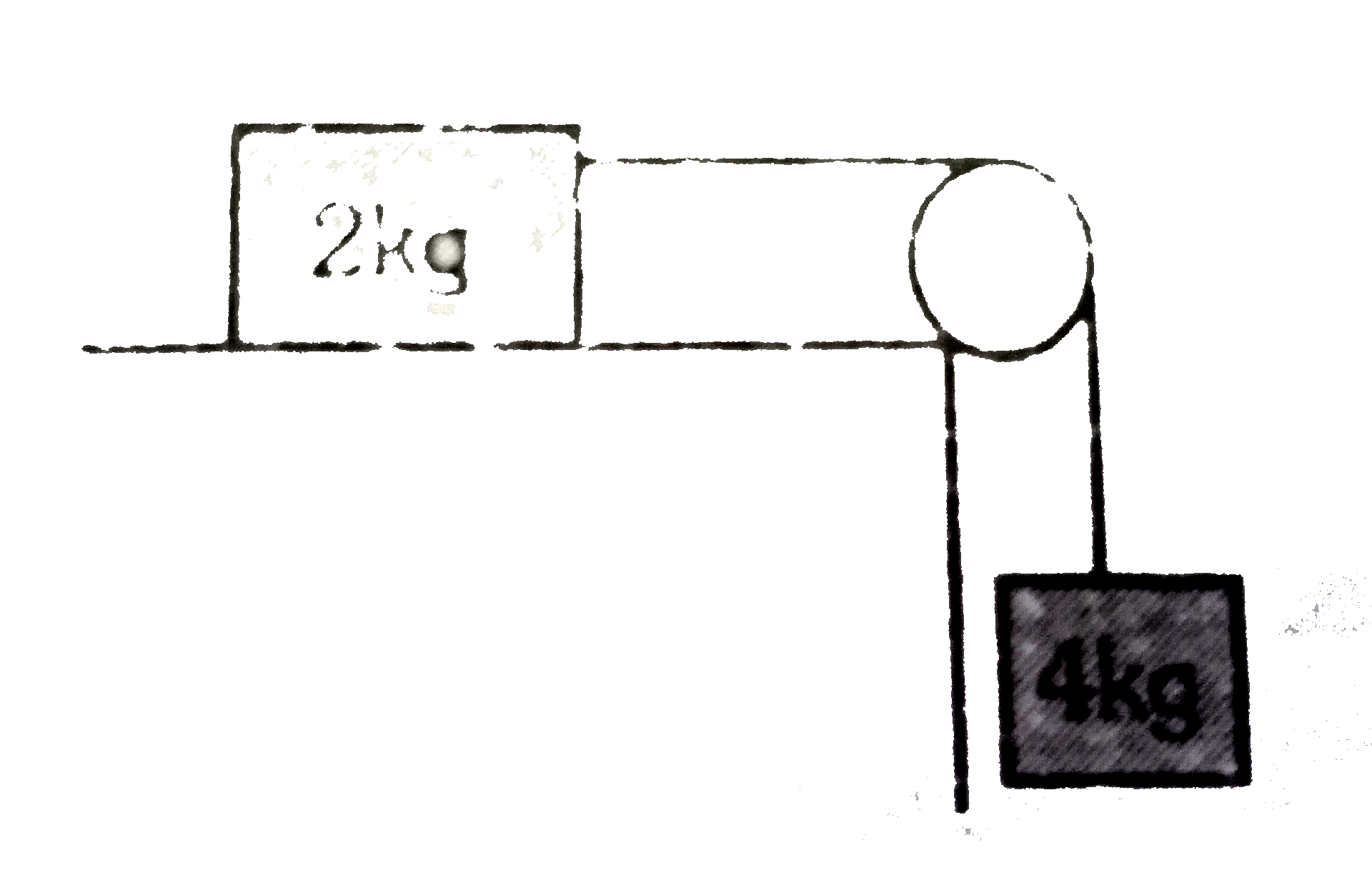
View SolutionA block on table shown in is just on the edge of slipping Find the coefficient of static friction between the blocks and table
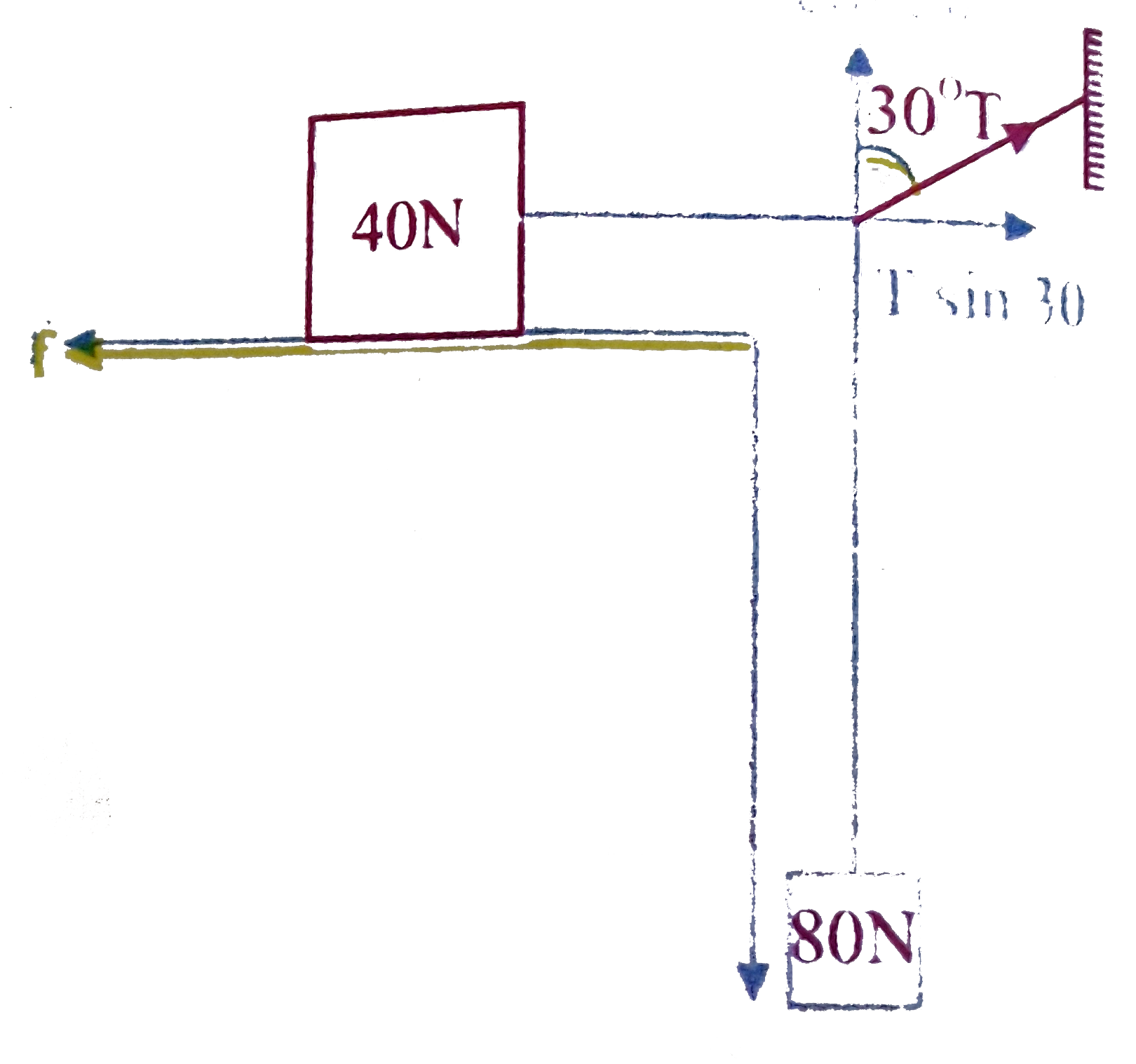 .
.
View Solution
Knowledge Check
A block A of mass m1 rests on a horizontal table. A light string connected to it passes over a frictionless pully at the edge of the table and from its other end another block B of mass m2 is suspended. The coefficient of kinetic friction between the block and the table is H. When the block A is sliding on the table, the tension in the string is
Am1m2(1+μk)g(m1+m2)Bm1m2(1−μk)g(m1)+m2C(m2+μkm1)g(m1+m2)D(m2−μkm1)g(m1+m2)A block of mass m1 rests on a horizontal table. A string tied to the block is passed on a frictionless pulley fixed at the end of the table and to the other end of string is hung another block of mass m2. The acceleration of the system is
Am2gm1+m2Bm1gm1+m2CgDm2gm1A block of mass m1 rests on a rough horizontal plane with coefficient of friction as μ. A light strin attached to this block passes over a light frictionless pulley and carries another block of mass m2 as shown in figure. If the system is just about to move, then find the value of μ.
 Am2cosθm1−m2sinαBm1sinαm1−m2sinαCm2cosαm1+μ2sinαDm1sinαm1+m2sinα
Am2cosθm1−m2sinαBm1sinαm1−m2sinαCm2cosαm1+μ2sinαDm1sinαm1+m2sinα
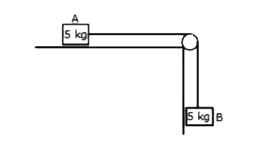
A block of mass 5 kg resting on a horizontal surface is connected by a cord, passing over a light frictionless pulley to a hanging block of mass 5 kg. The coefficient of kinetic friction between the block and the surface is 0.5. Tension in the cord is (g=9.8m/s2 )
View SolutionA block of mass m is kept on a horizontal table. If the static friction coefficient is μ., find the frictional force acting on the block.
View SolutionA block A of mass m1 is placed on a horizontal frictionless table. It is connected to one end of a light spring of force constant k whose other end is fixed to a wall. A small block B of mass m2 is placed on block A. The coefficient of static friction between the blocks is μ. The system is displaced slightly from its equilibrium position and released. What is the maximum amplitude of the resulting simple harmonic motion of the system so that the upper block does not slip over the lower block ?
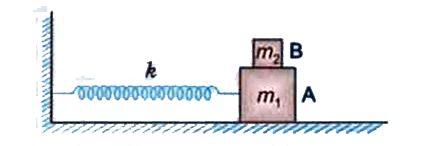
View Solution
Two blocks of mass M and 3M (in kg) are connected by an inextensible light thread which passes over a light frictionless pulley. The whole system is placed over a fixed horizontal table as shown.The coefficient of friction between the blocks and table surface is μ. The pulley is pulled by a string sttached to its centre and accelerated to left with acceleration a(ms2). Assume that gravity acts with constant acceleration g(ms2) downwards through the plane of table. Then:
(a) Find the forizontal accelration of both the blocks (Assume that both the blocks are moving.)
(b) What is the maximum acceleration a, for which the block of mass 3 M will remain stationary?
View SolutionFour blocks are connected with a.string passing over a frictionless pulley fixed at the corner of a table as shown in figure. The coefficient of static friction of A with table is 0.50. The minimum mass m of the block, so that blocks do not move should be ...... kg.
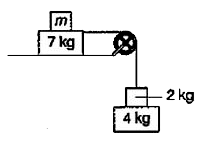
View Solution
