The separation between C and O atoms in CO is 1.2 A. The distance of carbon atom from the centre of mass is
0.3∘A
0.7∘A
0.5∘A
0.9∘A
To find the distance of the carbon atom from the center of mass of the CO molecule, we can follow these steps:
Step 1: Identify the masses of the atoms
- The mass of the carbon atom (C) is approximately 12 atomic mass units (amu).
- The mass of the oxygen atom (O) is approximately 16 atomic mass units (amu).
Step 2: Define the positions of the atoms
- Let's place the carbon atom at the origin (0, 0) on the x-axis.
- The oxygen atom will then be at a distance of 1.2 Å from the carbon atom, which means its position is (1.2, 0).
Step 3: Use the formula for the center of mass (CM)
The formula for the center of mass (CM) along the x-axis is given by:
xCM=∑(mi⋅xi)∑mi
Where:
- mi is the mass of each atom,
- xi is the position of each atom.
Step 4: Substitute the values into the formula
- For carbon (C): m1=12amu,x1=0
- For oxygen (O): m2=16amu,x2=1.2Å
Now substituting these values into the formula:
xCM=(12⋅0)+(16⋅1.2)12+16
Step 5: Calculate the numerator and denominator
- Numerator: 12⋅0+16⋅1.2=0+19.2=19.2
- Denominator: 12+16=28
Step 6: Calculate the center of mass
Now we can calculate xCM:
xCM=19.228≈0.6857Å
Step 7: Find the distance of the carbon atom from the center of mass
The distance of the carbon atom from the center of mass is given by:
Distance from C to CM=1.2−xCM
Substituting the value of xCM:
Distance from C to CM=1.2−0.6857≈0.5143Å
Step 8: Round off the answer
Rounding off 0.5143Å gives approximately 0.5Å.
Final Answer
The distance of the carbon atom from the center of mass is approximately 0.5 Å.
---
- The mass of the carbon atom (C) is approximately 12 atomic mass units (amu).
- The mass of the oxygen atom (O) is approximately 16 atomic mass units (amu).
- Let's place the carbon atom at the origin (0, 0) on the x-axis.
- The oxygen atom will then be at a distance of 1.2 Å from the carbon atom, which means its position is (1.2, 0).
The formula for the center of mass (CM) along the x-axis is given by:
- mi is the mass of each atom,
- xi is the position of each atom.
- For carbon (C): m1=12amu,x1=0
- For oxygen (O): m2=16amu,x2=1.2Å
- Numerator: 12⋅0+16⋅1.2=0+19.2=19.2
- Denominator: 12+16=28
Now we can calculate xCM:
The distance of the carbon atom from the center of mass is given by:
Rounding off 0.5143Å gives approximately 0.5Å.
The distance of the carbon atom from the center of mass is approximately 0.5 Å.
Topper's Solved these Questions
- System of particles & rotational MotionBOOK - SL ARORACHAPTER - System of particles & rotational MotionEXERCISE - EXERCISE
353 Videos
- ROTATIONAL MOTIONBOOK - SL ARORACHAPTER - ROTATIONAL MOTIONEXERCISE - Problem for self practice
90 Videos
- Thermal Properties of MatterBOOK - SL ARORACHAPTER - Thermal Properties of MatterEXERCISE - Exercise
449 Videos
Similar Questions
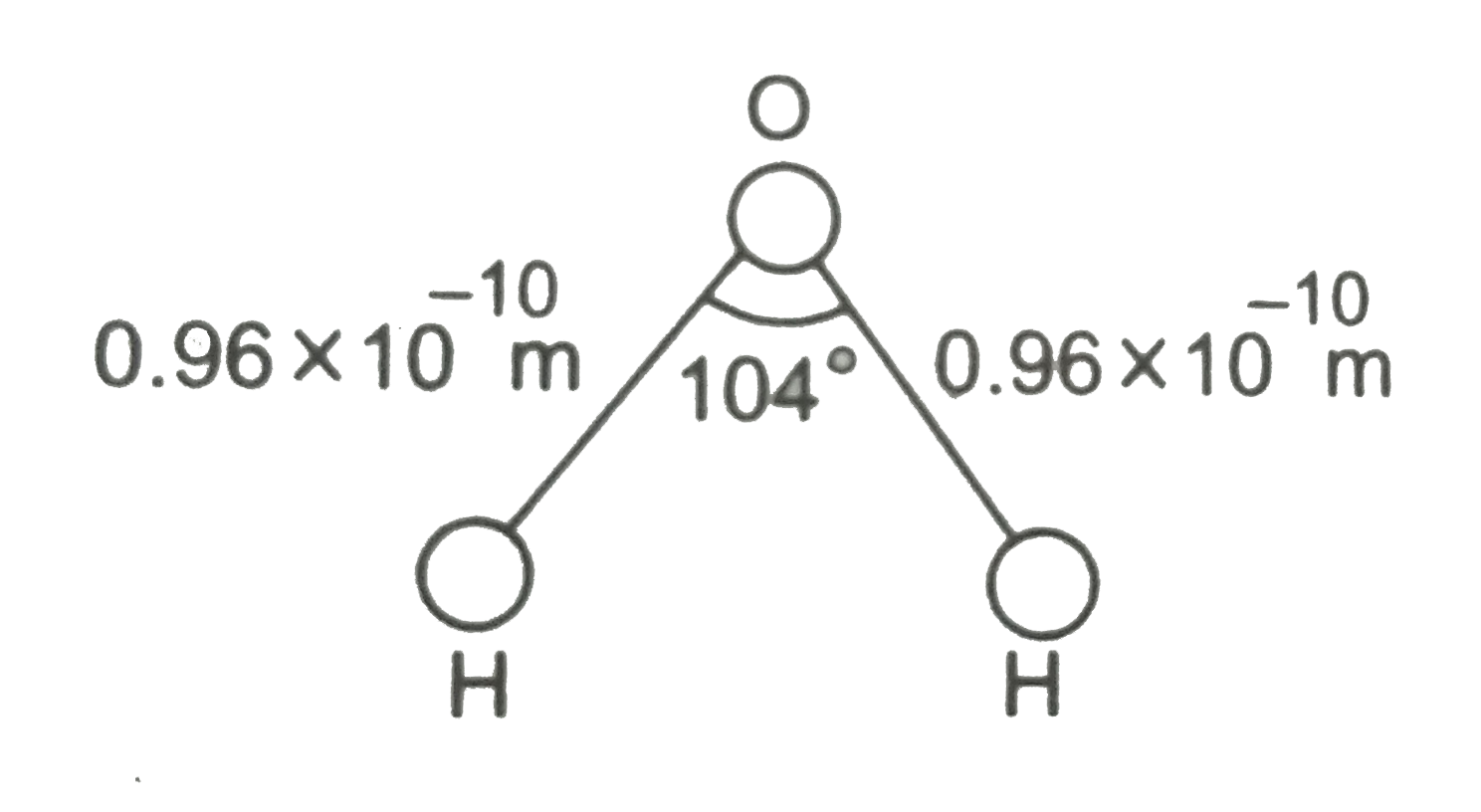
The structure of a water molecule is shown in figure. Find the distance of the distance of the centre of mass of the molecule from the centre of the oxygen atom.
View SolutionIn a carbon monoxide molecule, the carbon and oxygen atoms are separated by a distance of 1.12×10−10 m. The distance of the centre of mass from the carbon atom is
View Solution
Knowledge Check
The distance of centre of mass from O is
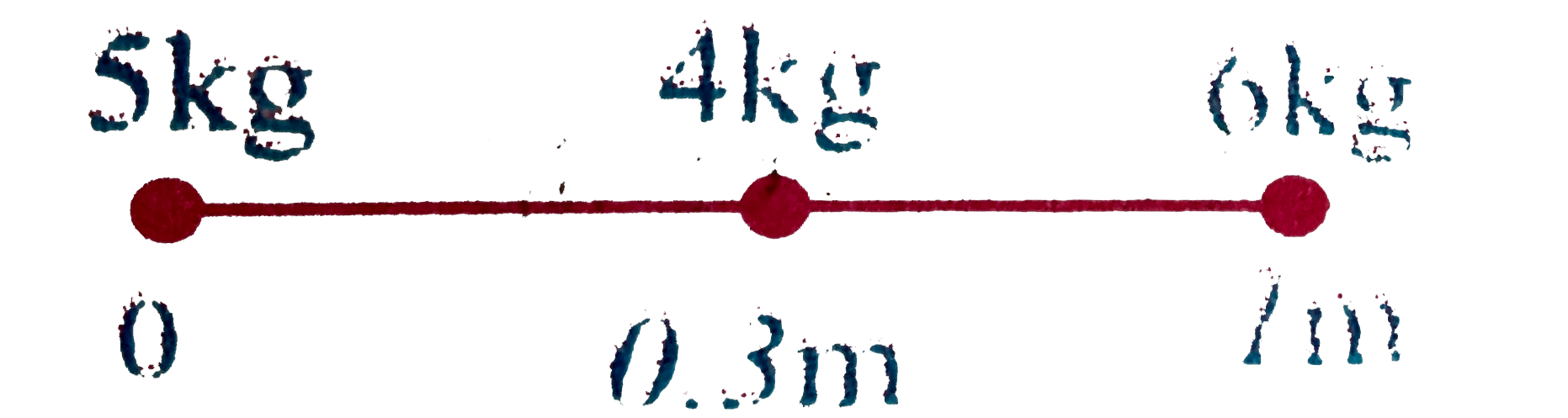 A0.21mB0.35mC0.42mD0.48m
A0.21mB0.35mC0.42mD0.48mConsider a system of two spheres of masses 5 kg and 25 kg. The distance between their centres is 1.2 m. What is the distance of their centre of mass from the centre of the sphere of mass 5 g?
A0.5mB0.6mC08mD1mIn a carbon monoxide molecule, the carbon and the oxygen atoms are separated by a distance 1.2×10−10m. The distance of the centre of mass from the carbon atom is
A0.48×10−10mB0.51×10−10mC0.74×10−10mD0.68×10−10m
In a carbon monoxide molecule, the carbon and the oxygen atoms are separted by a distance 1.12×1010 m. The distance of the centre of mass from the carbon atom is
View SolutionTwo hydrogen atoms are located at the distances r1 and r2 from origin. Their centre of mass is at
View SolutionTwo bodies of masses m1 and m2 are separated by a distance R. The distance of the centre of mass of the bodies from the mass m1 is
View SolutionTwo bodies of masses m1 and m2 are separated by a distance R. The distance of the centre of mass of the bodies from the mass m1 is
View SolutionA compound (molar mass = 120 g ) contains 40% carbon by mass. If the ration of number of H and O
atoms in the compound is 2 : 1, then number of H- atoms in one molecule of the compound is :-
View Solution
