The centre of mass of a solid cone along the line form the center of the base to the vertex is at
one-fourth of the height
one-third of the height
one-fifth of the height
) none of the above
Step by step video & image solution for The centre of mass of a solid cone along the line form the center of the base to the vertex is at by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- System of particles & rotational MotionBOOK - SL ARORACHAPTER - System of particles & rotational MotionEXERCISE - EXERCISE
353 Videos
- ROTATIONAL MOTIONBOOK - SL ARORACHAPTER - ROTATIONAL MOTIONEXERCISE - Problem for self practice
90 Videos
- Thermal Properties of MatterBOOK - SL ARORACHAPTER - Thermal Properties of MatterEXERCISE - Exercise
449 Videos
Similar Questions
Find the centre of mass of a uniform solid cone.
View SolutionA uniform solid right circular cone of base radius R is joined to a uniform solid hemisphere of radius R and of the same density, as shown in the figure. The centre of mass of the.composite solid lies at the centre of base of the cone. The height of the cone is √xR. Find x.
'(##CEN_KSR_PHY_JEE_C08_E01_017_Q10##)'
View Solution
Knowledge Check
A uniform solid right circular cone of base radius R is joined to a uniform solid hemisphere of radius R and of the same density, as shown. The centre of mass of the composite solid lies at the centre of base of the cone. The height of the cone is
 A1.5RB√3RC3RD2√3R
A1.5RB√3RC3RD2√3RDistance of the centre of mass of a solid uniform cone from its vertex is z0 . If the radius of its base is R and its height is h then z0 is equal to:
Ab24RB3b4C5h8D3h28RA solid hemisphere and a solid cone have a common base and are made of same material. The centre of mass of the common structure coincides with the centre of the common base. If R is the radius of hemisphere and h is height of the cone, then
 AhR=√3BhR=1√3ChR=3DhR=13
AhR=√3BhR=1√3ChR=3DhR=13
Height the length of the line segment joining the vertex to the center of the base is called the height of the cone.
View SolutionFind the distance of centre of mass of a uniform cone of height 'h' and base radius R, from the vertex on the line of symmetry .
View SolutionA solid of uniform density is made of a hemisphere and a right circular cone which have a common base of radius r . Determine the value of h of the cone if the CG of the system is at the centre of the base.
View SolutionDistance of the centre of mass of a solid uniform cone from its vertex is z0 . If the radius of its base is R and its height is h then z0 is equal to:
View SolutionA uniform solid right circular cone of base radius R is joined to a uniform solid hemisphere of radius R and of the same density, so as to have a common face. The centre of mass of the composite solid lies on the common face. The height of the cone is:
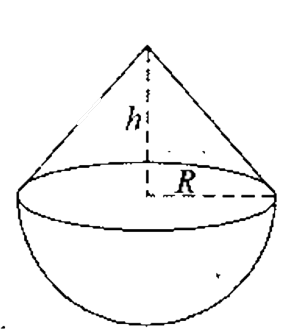
View Solution
