Two closed bulbs of equal volume (V) containing an ideal gas initially at pressure $p_{i}$ and temperature $T_{1}$ are connected through a narrow tube of negligible volume as shown in the figure below. The temperature of one of the bulbs is then raised to $T_{2}$ . The final pressure $p_{f}$ is :

$2 p_{i} (\frac{T_{1} T_{2}}{T_{1} + T_{2}})$

$p_{i} (\frac{T_{1} T_{2}}{T_{1} + T_{2}})$

$2 p_{i} (\frac{T_{1}}{T_{1} + T_{2}})$

$2 p_{i} (\frac{T_{2}}{T_{1} + T_{2}})$

Text Solution

Verified by Experts

The correct Answer is:D

Updated on:21/07/2023

Two closed bulb of euqal volume (V) containing an ideal gas initially at pressure $p_{i}$ and Temperature $T_{1}$ are connected through a narrow tube of negligible volume as shown in the figure below. The temperature of one of the bulbs is then released to $T_{2}$ . The final pressure $p_{t}$ is :

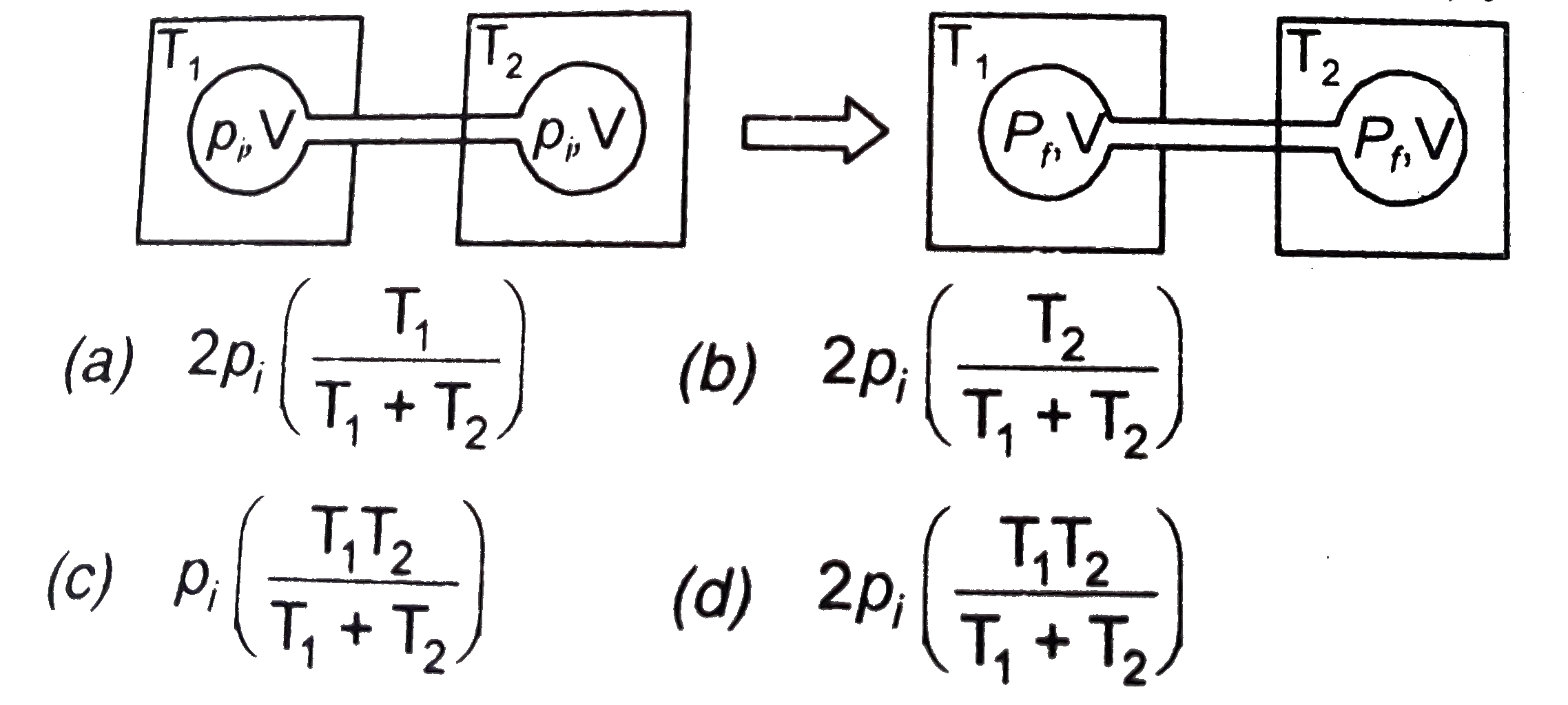A $2 p_{i} (\frac{T_{1}}{T_{1} + T_{2}})$
B $2 p_{i} (\frac{T_{2}}{T_{1} + T_{2}})$
C $p_{i} (\frac{T_{1} T_{2}}{T_{1} + T_{2}})$
D $2 p_{i} (\frac{T_{1} T_{2}}{T_{1} + T_{2}})$
Two closed vessels of equal volume containing air at pressure $P_{1}$ and temperature $T_{1}$ are connected to each other through a narrow tube. If the temperature in one of the vessels is now maintained at $T_{1}$ and that in the other at $T_{2}$ , what will be the pressure in the vessels?
A $\frac{2 P_{1} T_{1}}{T_{1} + T_{2}}$
B $\frac{T_{1}}{2 P_{1} T_{2}}$
C $\frac{2 P_{1} T_{2}}{T_{1} + T_{2}}$
D $\frac{2 P_{1}}{T_{1} + T_{2}}$
Two closed vessels of equal volume containing air at pressure $P_{1}$ and temperature $T_{1}$ are connected to each other through a narrow tube. If the temperature in one of the vessels is now maintained at $T_{1}$ and that in the other at $T_{2}$ , what will be the pressure in the vessels?
A $\frac{2 P_{1} T_{1}}{T_{1} + T_{2}}$
B $\frac{T_{1}}{2 P_{1} T_{2}}$
C $\frac{2 P_{1} T_{2}}{T_{1} + T_{2}}$
D $\frac{2 P_{1}}{T_{1} + T_{2}}$