Using constraint equations find the relation between a1anda2

Text Solution
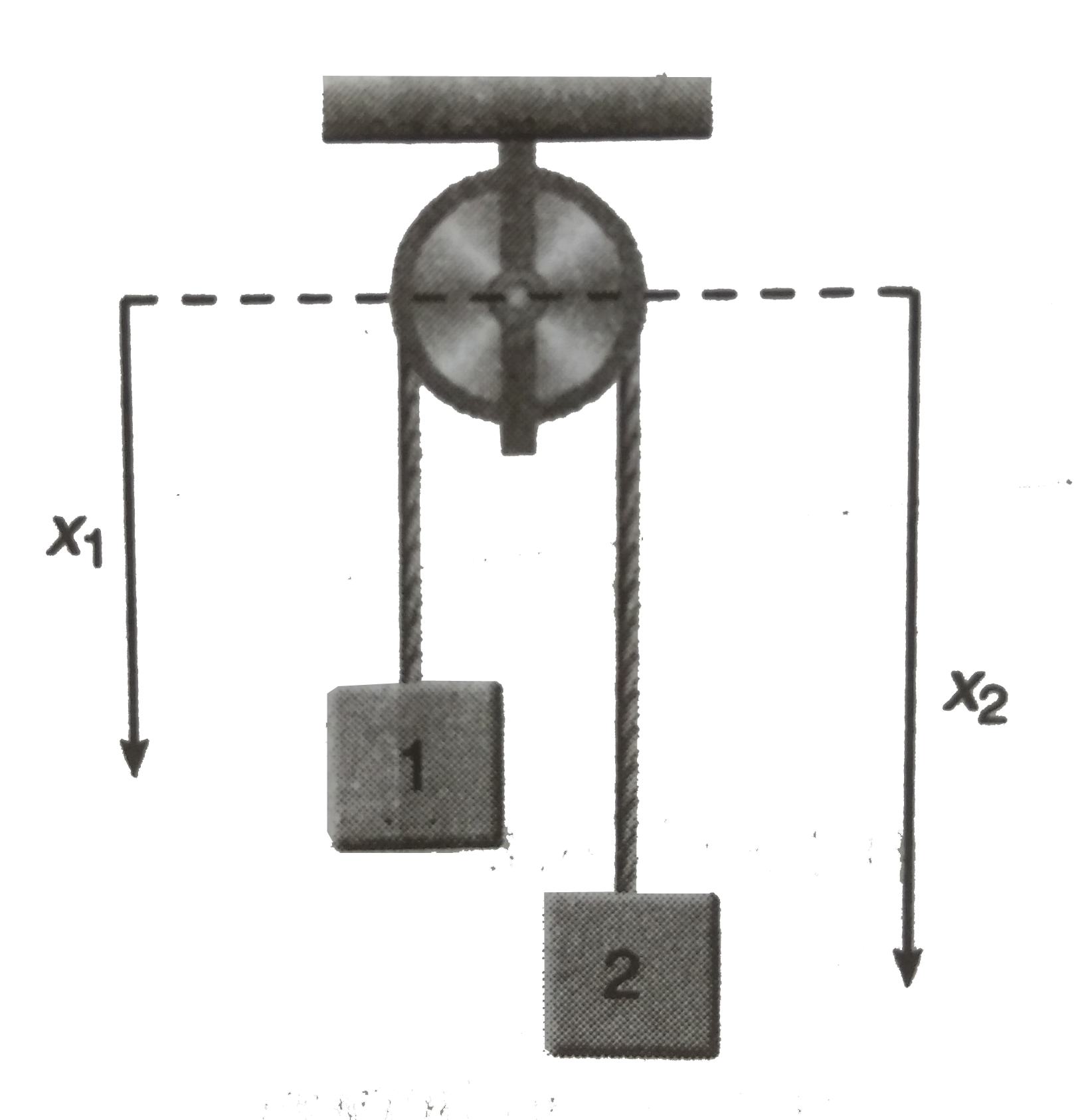
Point 1,2,3 and 4 are movable. Let their dis-placement from a fixed line be x1,x2,x3andx4
x1+x3=l1
(x1−x3)+(x4−x3)=l2
(x1−x4)+(x2−x4)=l3
On double differentiating with respect to time ,
we will get following three constraint relations :
a1+a3=0 ....... (i)
a1+a4−2a3=0........ (ii)
a1+a2−2a4=0............ (iii)
Solving Eqs. (i) ,(ii) and (iii) , we get a2=−7a1
Which is the desired relation between a1anda2

|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - LAWS OF MOTIONEXERCISE - LONG ANSWER TYPE QUESTIONS2videos
LAWS OF MOTION
- BOOK - AAKASH SERIESCHAPTER - LAWS OF MOTIONEXERCISE - SHORT ANSWER TYPE QUESTION2videos
LAWS OF MOTION
- BOOK - AAKASH SERIESCHAPTER - KINETIC THEORY OF GASESEXERCISE - Practice Exercise15videos
KINETIC THEORY OF GASES
- BOOK - AAKASH SERIESCHAPTER - MECHANICAL PROPERTIES OF FLUIDS EXERCISE - EXERCISE-343videos
MECHANICAL PROPERTIES OF FLUIDS
Similar Questions
Knowledge Check
- Question 1 - Select One
Two AMs.A1 and A2, two GMs. G1 and G2 and two HMs. H1 and H2 are inserted between any two numbers. Then find the arithmetic mean between H1 and H2 in terms of A1,A2,G1,G2.
AA1+A22G1G2BA1−A22G1G2CA1+A22+G1G2DG1+G22A1A2 - Question 2 - Select One
If the equation of the locus of a point equidistant from the points (a1,b1) and (a2,b2) is (a1−a2)x+(b2+b2)y+c=0, then the value of C is
Aa21−a22+b21−b22B√a21+b21−a22−b22C12(a21+a22+b21+b22)D12(a21+b22+a21+b22) - Question 3 - Select One
Two concentric conducting spherical shells of radii a1anda2(a2>a1) are charged to potentials ϕ1 and ϕ2, respectively. Find the charge on the inner shell.
Aq1=4πε0(ϕ1−ϕ2a2−a1)a1a2Bq1=4πε0(ϕ1+ϕ2a2+a1)a1a2Cq1=πε0(ϕ1−ϕ2a2+a1)a1a2Dq1=2πε0(ϕ1+ϕ2a2−a1)a1a2
Using constraint method find the relation between accelerations of 1 and 2.
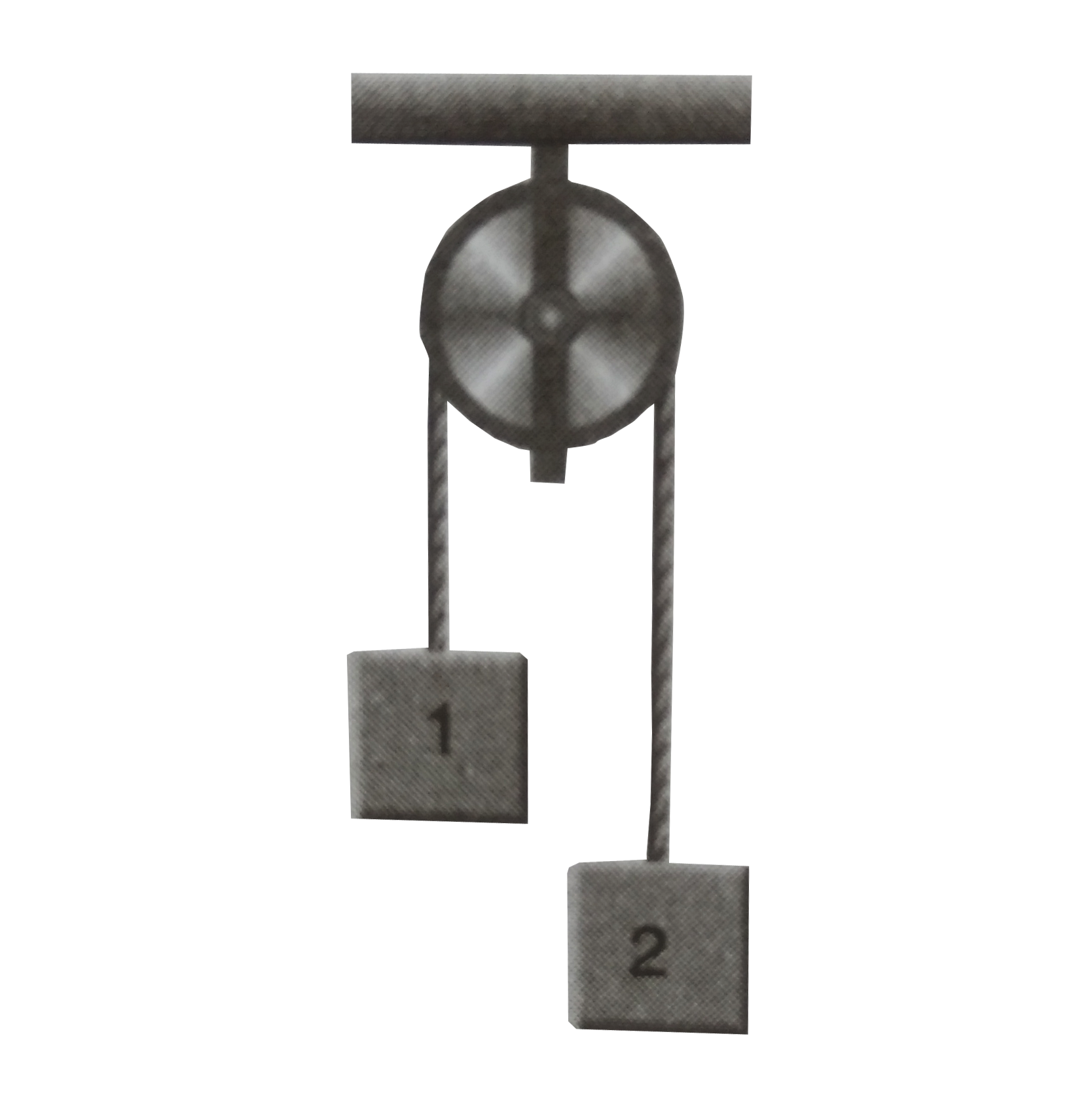
 View Solution
View SolutionUsing constraint method find the relation between accelerations of 1 and 2.
 View Solution
View SolutionIf the equation of the locus of a point equidistant from the points (a1,b1) and (a2,b2) is (a1−a2)x+(b1−b2)y+c=0 , then the value of c is aa2−a22+b12−b22 √a12+b12−a22−b22 12(a12+a22+b12+b22) 12(a22+b22−a12−b12)
View SolutionIf the equation of the locus of a point equidistant from the points (a1,b1) and (a2,b2) is (a1−a2)x+(b1−b2)y+c=0 , then find the value of c.
View SolutionIf the equation of the locus of a point equidistant from the points (a1,b1) and (a2,b2) is (a1−a2)x+(b2+b2)y+c=0, then the value of C is
View Solution


