Two identical pith balls each of mass .m. holding charge .q. each are suspended by silk threads of equal length from same point. They move apart due to repulsion. If the separation between the two balls is 2x and each string makes small angle $θ$ to the vertical,

Text Solution

Verified by Experts

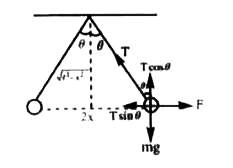
From fig $T cos θ = m g, T sin θ = F$
$\frac{F}{m g} = tan θ = \frac{x}{\sqrt{1^{2} - x^{2}}}$ If $θ$ is small $Tan θ = sin θ \approx θ = \frac{x}{1}, \frac{F}{m g} \frac{x}{1}$
Where $F = \frac{1}{4 π \in_{0}} \frac{q^{2}}{4 x^{2}} \Rightarrow \frac{q^{2}}{16 π \in_{0} x^{2} m g} = \frac{x}{1}$
$\Rightarrow x = {(\frac{q^{2} 1}{16 π \in_{0} m g})}^{1 / 3}$
$\Rightarrow$ Tension in the string $T = \sqrt{F^{2} + {(m g)}^{2}}$
In the above case if the balls are suspended in a liquid of density $ρ$ and the distance between the balls remains the same, then
$\frac{F}{m g} = \frac{F^{1}}{m g^{1}} \Rightarrow \frac{F}{F^{1}} = \frac{m g}{m g^{1}} \Rightarrow \frac{m g}{m g (1 - \frac{ρ}{d})} (∵ k = \frac{F_{a}}{F_{m}})$
$\Rightarrow (1 - \frac{ρ}{d}) = \frac{1}{K} or K = \frac{d}{(d - p)}$
(d is density of material of the ball)
$\Rightarrow$ In the above case if the charges on teh two balls are different and the angles made by those two strings to the vertical are $θ_{1} and θ_{2}$ respectively, then $θ_{1} = θ_{2}$ (as F, mg are same ) if $m_{1} > m_{2} then θ_{1} < θ_{2}$
$\Rightarrow$ In the above application if the whole setup is kept in an artifical satellite (in zero gravity region) the angle between the two strings is $180^{\circ}$ and tension in each string is $\frac{1}{4 π \in_{0}} \frac{q^{2}}{41^{2}}$

Updated on:21/07/2023

Two identical small bodies each of mass m and charge q are suspended from two strings each of length l from a fixed point. This whole system is taken into an orbiting artificial satellite, then find the tensio in strings
A $\frac{K q^{2}}{l^{2}} + 2 m g$
B $\frac{K q^{2}}{4 l^{2}} + 2 m g$
C $\frac{K q^{2}}{l^{2}}$
D $\frac{K q^{2}}{4 l^{2}}$
Two identical tennis balls each having mass 'm' and charge 'q' are suspended from a fixed point by threads of length 'l'. What is the equilibrium separation when each thread makes a small angle $' θ'$ with the vertical ?
A $x = {(\frac{q^{2} l}{2 π ε_{0} m g})}^{1 / 2}$
B $x = {(\frac{q^{2} l}{2 π ε_{0} m g})}^{1 / 3}$
C $x = {(\frac{q^{2} l^{2}}{2 π ε_{0} m^{2} g})}^{1 / 3}$
D $x = {(\frac{q^{2} l^{2}}{2 π ε_{0} m^{2} g^{2}})}^{1 / 3}$