Two identical small bodies each of mass m and charge q are suspended from two strings each of length l from a fixed point. This whole system is taken into an orbiting artificial satellite, then find the tensio in strings
Kq2l2+2 mg
Kq24l2+2 mg
Kq2l2
Kq24l2
To solve the problem of finding the tension in the strings when two identical small bodies, each of mass m and charge q, are suspended in an orbiting artificial satellite, we can follow these steps:
1. Understanding the Situation:
- We have two identical small bodies, each with mass m and charge q, suspended from two strings of length l.
- The system is in an orbiting artificial satellite, which means that gravitational forces are negligible (effectively zero).
2. Identifying Forces:
- In the absence of gravity, the only forces acting on the bodies are the electrostatic repulsive forces due to their charges and the tension in the strings.
- The bodies will repel each other due to their like charges.
3. Geometry of the Setup:
- When the bodies are in equilibrium, they will be at a certain angle due to the repulsive force. However, since we are in a zero-gravity environment, the tension in the strings will balance the electrostatic force directly.
4. Calculating the Electrostatic Force:
- The electrostatic force F between the two charges can be calculated using Coulomb's law:
F=kq2r2
- Here, k is Coulomb's constant, q is the charge of each body, and r is the distance between the two charges.
5. Finding the Distance Between Charges:
- When the bodies are at equilibrium, the distance r between them can be related to the length of the strings l. If the angle between the strings is small, we can approximate:
r≈lsin(θ)(where θ is the angle each string makes with the vertical)
- For small angles, sin(θ)≈θ, and if the angle is such that the distance is approximately l, we can simplify this to r≈l.
6. Setting Up the Tension Equation:
- Since the only force acting on the bodies is the electrostatic repulsion, we can set the tension T in the strings equal to the electrostatic force:
T=F
7. Substituting for Tension:
- Substituting the expression for the electrostatic force into the tension equation:
T=kq2(2l)2
- Here, r=2l because the distance between the two charges is twice the length of the string when they are at equilibrium.
8. Final Expression for Tension:
- Therefore, we can express the tension in the strings as:
T=kq24l2
Conclusion:
The tension in the strings when the system is in an orbiting artificial satellite is given by:
T=kq24l2
- We have two identical small bodies, each with mass m and charge q, suspended from two strings of length l.
- The system is in an orbiting artificial satellite, which means that gravitational forces are negligible (effectively zero).
- In the absence of gravity, the only forces acting on the bodies are the electrostatic repulsive forces due to their charges and the tension in the strings.
- The bodies will repel each other due to their like charges.
- When the bodies are in equilibrium, they will be at a certain angle due to the repulsive force. However, since we are in a zero-gravity environment, the tension in the strings will balance the electrostatic force directly.
- The electrostatic force F between the two charges can be calculated using Coulomb's law:
F=kq2r2
- Here, k is Coulomb's constant, q is the charge of each body, and r is the distance between the two charges.
- When the bodies are at equilibrium, the distance r between them can be related to the length of the strings l. If the angle between the strings is small, we can approximate:
r≈lsin(θ)(where θ is the angle each string makes with the vertical)
- For small angles, sin(θ)≈θ, and if the angle is such that the distance is approximately l, we can simplify this to r≈l.
- Since the only force acting on the bodies is the electrostatic repulsion, we can set the tension T in the strings equal to the electrostatic force:
T=F
- Substituting the expression for the electrostatic force into the tension equation:
T=kq2(2l)2
- Here, r=2l because the distance between the two charges is twice the length of the string when they are at equilibrium.
- Therefore, we can express the tension in the strings as:
T=kq24l2
The tension in the strings when the system is in an orbiting artificial satellite is given by:
T=kq24l2
Similar Questions
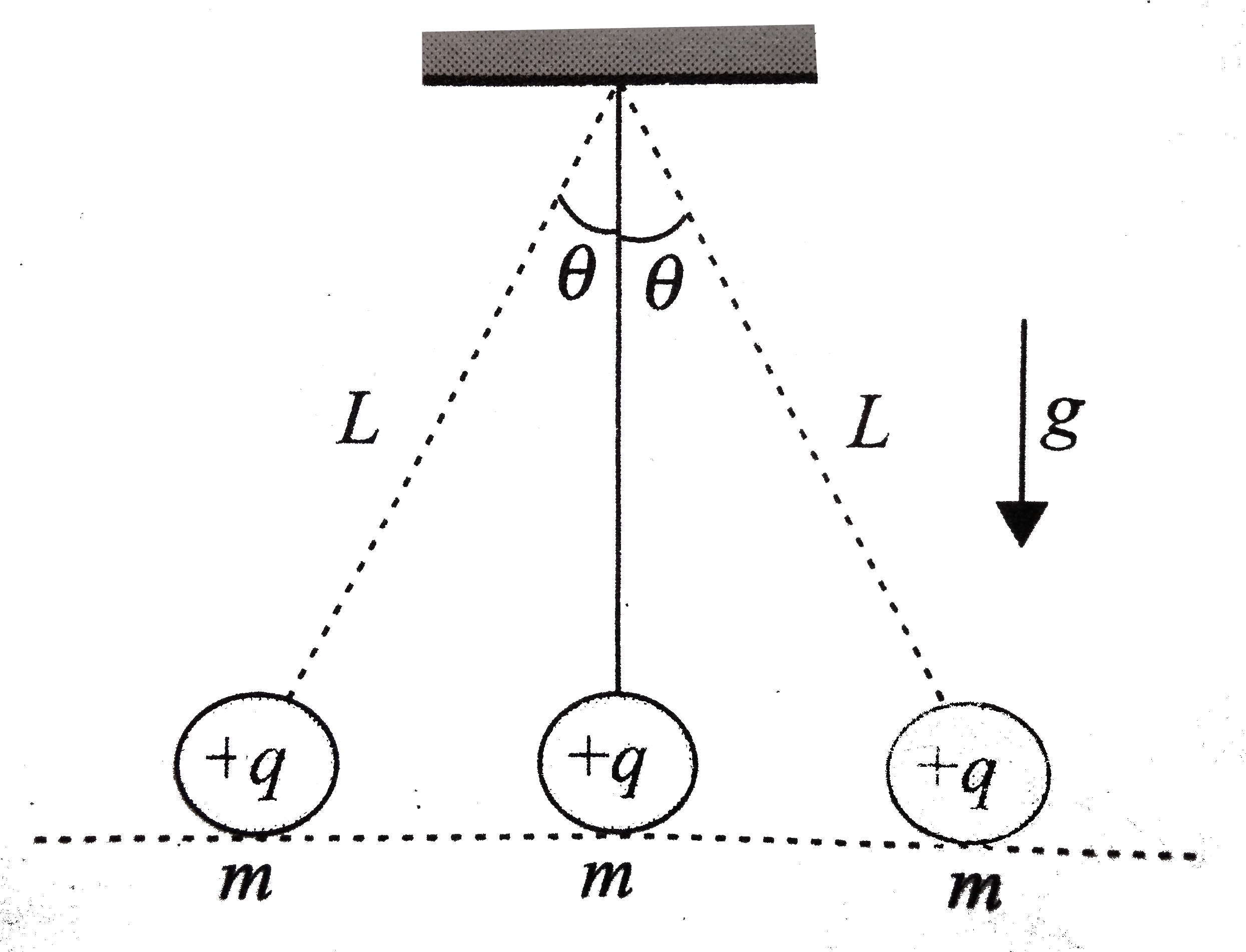
Three identical point charges, each of mass m and charge q, hang from three strings as shown in fig. The value of q in term of m, L, and q is
View SolutionTwo small balls having equal positive charge Q (coulumb) on each suspended by two insulating strings of equal length L (metre) from a hook fixed to a stand. The whole set-up is taken in a satellite into space where there is no gravity (state of weightlessness). Then tension (newtons) in each string is:
View SolutionTwo small balls having equal positive charge Q (coulumb) on each suspended by two insulating strings of equal length L (metre) from a hook fixed to a stand. The whole set-up is taken in a satellite into space where there is no gravity (state of weightlessness). Then tension (newtons) in each string is:
View SolutionTwo small balls having equal positive charge Q C on each are suspended by two insulating strings of equal length L metre, from a hook fixed to a stand. The whole setup is taken into space where there is no gravity (state of weightlessness). Then the angle θ between the two strings is
View SolutionTwo small balls having equal positive charge Q (coulumb) on each suspended by two insulating strings of equal length L (metre) from a hook fixed to a stand. The whole set-up is taken in a satellite into space where there is no gravity (state of weightlessness). Then tension (newtons) in each string is:
View SolutionA particle of mass m and charge q is fastened to one end of a string of length. The other end of the string is fixed to the point O. The whole sytem liles on as frictionless horizontal plane. Initially, the mass is at rest at A. A uniform electric field in the direction shown in then switfched on. Then

View SolutionA particle of mass m and charge q is fastened to one end of a string of length. The other end of the string is fixed to the point O. The whole sytem liles on as frictionless horizontal plane. Initially, the mass is at rest at A. A uniform electric field in the direction shown in then switfched on. Then

View SolutionTwo identical pith balls, each carrying charge q, are suspended from a common point by two strings of equal length l. Find the mass of each ball if the angle between the strings is 2θ in equilibrium.
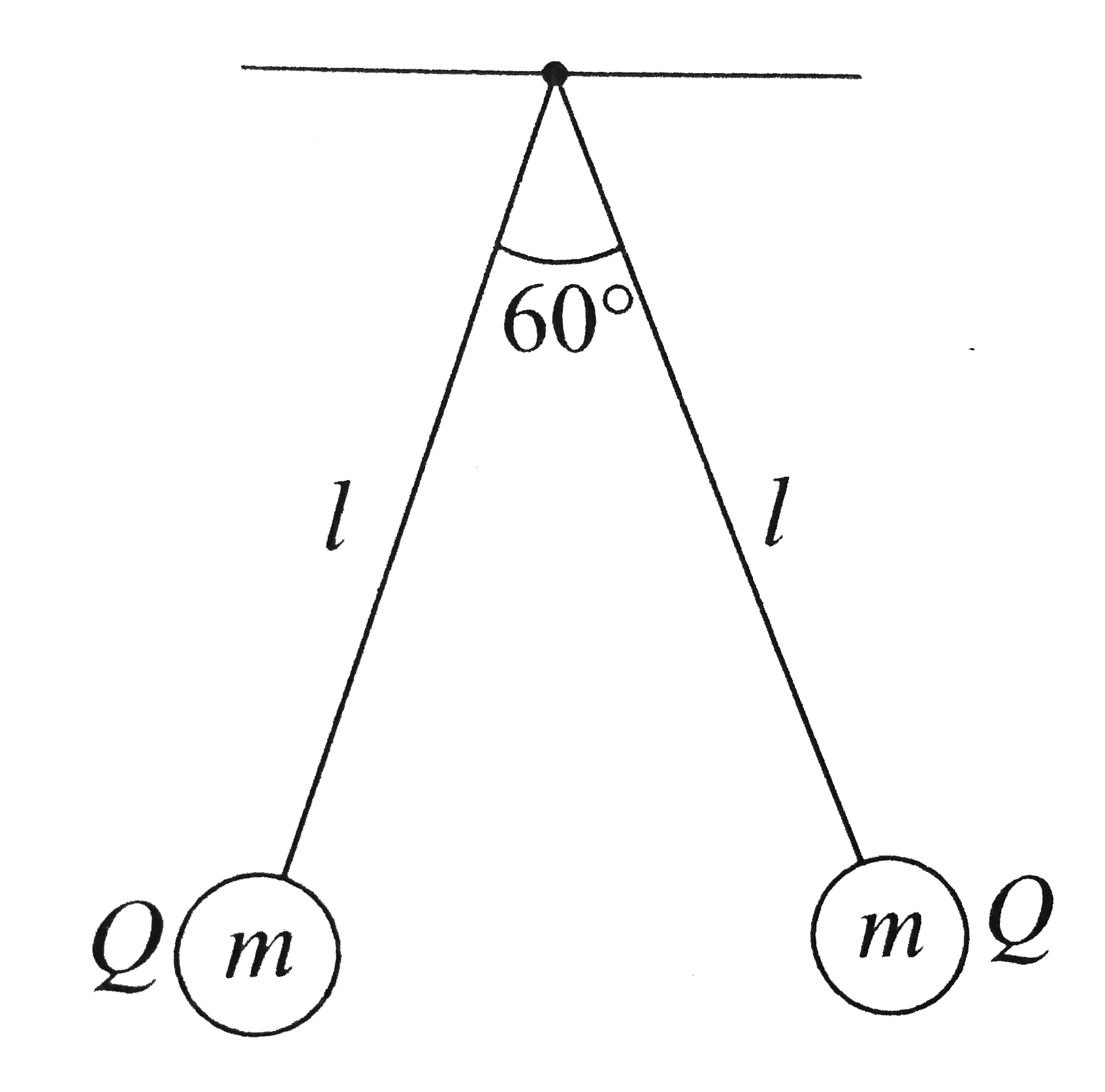
View SolutionTwo small balls, each having equal positive charge Q are suspended by two insulationg strings of equal length l from a hook fixed to a stand. It mass of each ball =m and total angle between the two strings is 60∘m, then find the charge on each ball.
View SolutionTwo charged particles having charge 2.0×10−8C each are joined by an insulating string of length 1 m and the system is kept on a smooth horizontal table. Find the tension in the string.
View Solution
