The capacitance of a parallel plate condenser, with plate area A and distance between plates d, when filed with a dielectric whose dielectric constant varies as, is ε(x)=ε0+βx. for 0<x<d2ε(x)=ε0+β(d−x) for d2<x<d
βA2loge(∈0βd2)
A2loge⎛⎜⎝∈0βd2⎞⎟⎠
A2loge⎛⎜⎝∈0∈0−βd2⎞⎟⎠
βA2∈0loge(∈0+βd2∈0)
The correct Answer is:D
Topper's Solved these Questions
- CAPACITORS BOOK - AAKASH SERIESCHAPTER - CAPACITORS EXERCISE - LECTURE SHEET (EXERCISE - IV) (LEVEL - II (ADVANCED)) Straight Objective Type Questions)
4 Videos
- CAPACITORS BOOK - AAKASH SERIESCHAPTER - CAPACITORS EXERCISE - LECTURE SHEET (EXERCISE - IV) (LEVEL - II (ADVANCED)) (More than one correct answer Type Questions )
3 Videos
- CAPACITORS BOOK - AAKASH SERIESCHAPTER - CAPACITORS EXERCISE - LECTURE SHEET (EXERCISE - III) (LEVEL - II (ADVANCED)) (Integer Type Questions )
3 Videos
- ATOMSBOOK - AAKASH SERIESCHAPTER - ATOMSEXERCISE - PRACTICE EXERCISE
21 Videos
- COMMUNICATION SYSTEM BOOK - AAKASH SERIESCHAPTER - COMMUNICATION SYSTEM EXERCISE - LECTURE SHEET (LEVEL - I) (MAIN) (EXERCISE - IV) (Straight Objective & More than one Correct Answer Type Questions)
20 Videos
Similar Questions
Calculate the capacitance of a parallel plate condenser, with plate area A and distance between plates d, when filled with a dielectric whose dielectric constant varies as,
K(x)=1+βx∈0 0<x<d2, K(x)=1+β∈0(d−x) d2<x<d.
For what value of β would the capacity of the condenser be twice that when it is without any dielectric?
View SolutionCalculate the capacitance of a parallel plate capacitor, with plate area A and distance between the plates d, when filled with a dielectric whose permittivity varies as
in(x)=in_(0)+kx(0 lt x lt (d)/(2)), in(x)=in_(0) +k(d-x)((d)/(2) lt x le d).
View Solution
Knowledge Check
A parallel plate capacitor has plates of area A separated by distance ‘d’ between them. It is filled with a dielectric which has a dielectric constant that varies as k(x)=K(1+ax) where ‘x’ is shown in figure. If (al)<<1 , the total capacitance of the system is best given by the expression:
 AAK∈0d(1+αl)BAk∈0d(1+αl2)CA∈0Kd(1+(αl2)2)DA∈0Kd(1+α2l22)
AAK∈0d(1+αl)BAk∈0d(1+αl2)CA∈0Kd(1+(αl2)2)DA∈0Kd(1+α2l22)
Calculate the capacitance of a parallel plate capacitor, with plate area A and distance between the plates d, when filled with a dielectric whose permittivity varies as
∈(x)=∈0+kx(0<x<d2),∈(x)=∈0+k(d−x)(d2<x≤d).
View SolutionA parallel plate capacitor with plate area 'A' and distance of separation 'd' is filled with a dielectric. What is the capacity of the capacitor when permittivity of the dielectric varies as : ε(x)=ε0+kx, for (0<x≤d2)
ε(x)=e0+k(d−x), for (d2≤x≤d)
View SolutionIn a parallel plate capacitor distance between the plate is 'd'. If dielectric of variable permeability is filled as
ε(x)=ε0+kx,0<x≤d2
ε(x)=ε0+k(d−x),d2<x≤d
Find capacitance.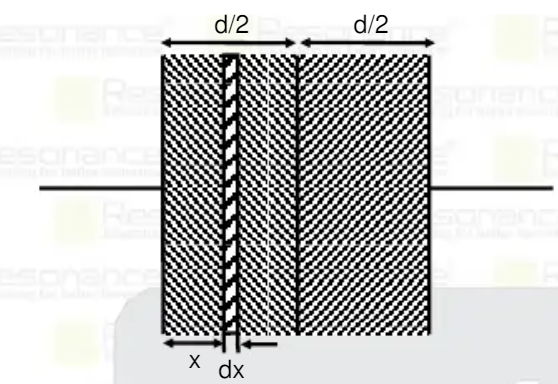
View SolutionA parallel plate capacitor with plate area A & plate separation d is filled with a dielectric material of dielectric constant given byK=K0(1+αx).. Calculate capacitance of system: (given αd<<1).

View SolutionA parallel plate capacitor with plate area A & plate separation d is filled with a dielectric material of dielectric constant given byK=K0(1+αx).. Calculate capacitance of system: (given αd<<1).

View SolutionA parallel plate capacitor with plate area A & plate separation d is filled with a dielectric material of dielectric constant given byK=K0(1+αx).. Calculate capacitance of system: (given αd<<1).

View SolutionA parallel plate capacitor with plate area A & plate separation d is filled with a dielectric material of dielectric constant given byK=K0(1+αx).. Calculate capacitance of system: (given αd<<1).

View Solution
