Calculate the capacitance of a parallel plate capacitor, with plate area A and distance between the plates d, when filled with a dielectric whose permittivity varies as
in(x)=in_(0)+kx(0 lt x lt (d)/(2)), in(x)=in_(0) +k(d-x)((d)/(2) lt x le d).
The correct Answer is:C=Aβ2ln(1+βd2∈0),βd=4∈0ln(1+βd2∈0). Solution of this equation gives required value of β.
To calculate the capacitance of a parallel plate capacitor filled with a dielectric whose permittivity varies, we will follow these steps:
Step 1: Understand the Configuration
We have a parallel plate capacitor with:
- Plate area A
- Distance between the plates d
- The dielectric permittivity varies as:
- For 0<x<d2: ϵ(x)=ϵ0+kx
- For d2<x≤d: ϵ(x)=ϵ0+k(d−x)
Step 2: Set Up the Capacitance for Each Section
The total capacitance C of the capacitor can be considered as two capacitors in series:
- The first capacitor C1 for the region 0<x<d2
- The second capacitor C2 for the region d2<x≤d
Step 3: Calculate the Differential Capacitance
For a small section dx of the capacitor, the differential capacitance dC can be expressed as:
dC1=ϵ(x)⋅Adx
For the first section:
dC1=(ϵ0+kx)⋅Adx
For the second section:
dC2=(ϵ0+k(d−x))⋅Adx
Step 4: Integrate to Find Total Capacitance
To find the total capacitance, we need to integrate dC1 from 0 to d2 and dC2 from d2 to d.
For C1:
C1=∫d20Aϵ0+kxdx
For C2:
C2=∫dd2Aϵ0+k(d−x)dx
Step 5: Solve the Integrals
1. For C1:
C1=A∫d201ϵ0+kxdx
The integral evaluates to:
C1=A(1kln(ϵ0+kx))d20=Ak(ln(ϵ0+kd2)−ln(ϵ0))
2. For C2:
C2=A∫dd21ϵ0+k(d−x)dx
The integral evaluates to:
C2=A(−1kln(ϵ0+k(d−x)))dd2=Ak(ln(ϵ0+kd2)−ln(ϵ0+kd))
Step 6: Combine the Results
Since C1 and C2 are in series, the equivalent capacitance C is given by:
1C=1C1+1C2
Step 7: Final Expression
After simplifying, we arrive at the final expression for the equivalent capacitance C:
C=kA2ln(ϵ0+kd2ϵ0)
We have a parallel plate capacitor with:
- Plate area A
- Distance between the plates d
- The dielectric permittivity varies as:
- For 0<x<d2: ϵ(x)=ϵ0+kx
- For d2<x≤d: ϵ(x)=ϵ0+k(d−x)
The total capacitance C of the capacitor can be considered as two capacitors in series:
- The first capacitor C1 for the region 0<x<d2
- The second capacitor C2 for the region d2<x≤d
For a small section dx of the capacitor, the differential capacitance dC can be expressed as:
dC1=ϵ(x)⋅Adx
For the first section:
dC1=(ϵ0+kx)⋅Adx
For the second section:
dC2=(ϵ0+k(d−x))⋅Adx
To find the total capacitance, we need to integrate dC1 from 0 to d2 and dC2 from d2 to d.
C1=∫d20Aϵ0+kxdx
C2=∫dd2Aϵ0+k(d−x)dx
1. For C1:
C1=A∫d201ϵ0+kxdx
The integral evaluates to:
C1=A(1kln(ϵ0+kx))d20=Ak(ln(ϵ0+kd2)−ln(ϵ0))
C2=A∫dd21ϵ0+k(d−x)dx
The integral evaluates to:
C2=A(−1kln(ϵ0+k(d−x)))dd2=Ak(ln(ϵ0+kd2)−ln(ϵ0+kd))
Since C1 and C2 are in series, the equivalent capacitance C is given by:
1C=1C1+1C2
After simplifying, we arrive at the final expression for the equivalent capacitance C:
C=kA2ln(ϵ0+kd2ϵ0)
Topper's Solved these Questions
- CAPACITANCEBook:RESONANCE ENGLISHChapter:CAPACITANCEExercise:Exercise - 3
Explore 26 Videos
- ATOMIC PHYSICSBook:RESONANCE ENGLISHChapter:ATOMIC PHYSICSExercise:Advanved level problems
Explore 17 Videos
- COMMUNICATION SYSTEMSBook:RESONANCE ENGLISHChapter:COMMUNICATION SYSTEMSExercise:Exercise 3
Explore 13 Videos
Similar Questions
Calculate the capacitance of a parallel plate capacitor, with plate area A and distance between the plates d, when filled with a dielectric whose permittivity varies as
in(x)=in_(0)+kx(0 lt x lt (d)/(2)), in(x)=in_(0) +k(d-x)((d)/(2) lt x le d).
View SolutionFind out the capacitance of parallel plate capacitor of plate area A and plate separation d.
View SolutionA parallel plate capacitor, with plate area A and plate separation d, is filled with a dielectric slabe as shown. What is the capacitance of the arrangement ?
View SolutionThe capacitance of the capacitors of plate areas A1 and A2(A1<A2) at a distance d is
View SolutionThe plates of a parallel plate capacitance 1.0 F are separated by a distance d =1 cm. Find the plate area .
View SolutionCalculate the capacitance of a parallel-plate capacitor having 20 cm x 20 cm square plates deparated by a distance of 1.0 mm.
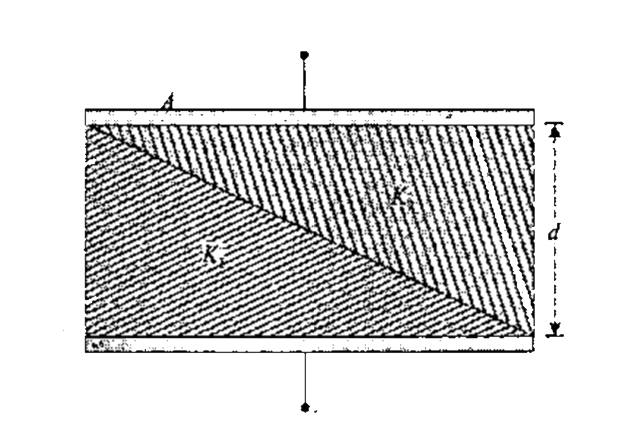
View SolutionThe capacitance of a parallel plate capacitor with plate area A and separation d is C. The space between the plates in filled with two wedges of dielectric constants K1 and K2 respectively. Find the capacitance of resulting capacitor.
View SolutionThe' distance between the plates of a parallel plate capacitor is d. A metal plate of thickness d/2 is placed between the plates. What will e its effect on the capacitance.
View SolutionThe force between the plates of a parallel plate capacitor of capacitance C and distance of separation of the plates d with a potential difference V between the plates, is.
View SolutionFind out equivalent capacitance between A and B. (take each plate Area = A and distance between two conjugative plates is d)

View Solution