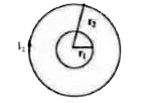
Two concentric circular coils, one of small radius r, and the other of large radius r2, such that r1<<r2 , are placed co-axially with centres coinciding. Obtain the mutual inductance of the arrangement.
Let a current I2 flow through the outer circular coil The field at the centre of the coil is B2=μ0I2/2r2 . Since the other co-axially placed coil has a very small radius, B may be considered constant over its cross-sectional area, Hence.
ϕ1=πr21B2=μ0πr212r2I2=M12I2 thus
mutual inductance of solenoid S1 with respect to S2
M12=μ0πr212r2......(i) but M12=M21=μ0πr212r2
Note that we calculated M12 from an approximate value of ϕ1 , assuming the magnetic field B2 to be uniform over the area πr21 . However we can accept this value because r1<<r2 ?
It would have been difficult to calculate the flux through the bigger coil of the non-uniform field due to the current in the smaller coil and hence the mutual inductance M12 The equality M12=M21 is helpful. Note also that mutual inductance depends solely on the geometry.
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - EXERCISE-IA
33 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - EXERCISE-IB
18 Videos
- ELECTRIC FIELD AND POTENTIALBOOK - AAKASH SERIESCHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - PROBLEMS (LEVEL-II)
32 Videos
- ELECTROMAGNETIC WAVESBOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - EXERCISE -II
20 Videos
Similar Questions
Two concentric circular coils, one of small radius r and the other of large radius R, such that R >> T, are placed coaxially with centres coinciding. Obtain the mutual inductance of the arrangement.
View SolutionTwo circular coils, one of smaller radius r1 and the other of very large radius r2 are placed co-axially with centres coinciding. Obtain the mutual inductance of the arrangement.
View Solution
Knowledge Check
Two concentric circular coils, one of small radius r1and the other of large radiusr2 such that r1<<r2 are placed coaxially with centres coinciding. Obtain the mutual inductance of the arrangement.
Aμ0πtr212r2Bμ0πtr222r1Cμ0πtr22r1Dμ0πtr21r2Two concentric co - planar circular loops of radius R and r(<<R) are placed as shown in the figure. The mutual inductance of the system will be
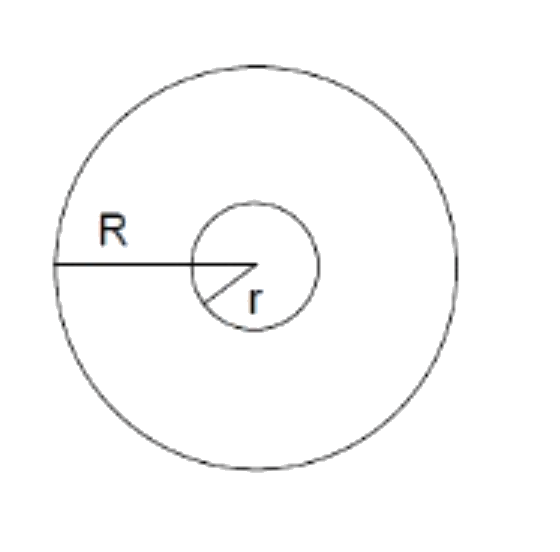 Aπμ0r22RBπμ0r24RCπμ0R24rDπμ0R22r
Aπμ0r22RBπμ0r24RCπμ0R24rDπμ0R22r
Two circular coils, one of smaller radius r1 and the other of very large radius r2 are placed co-axially with centres coinciding. Obtain the mutual inductance of the arrangement.
View Solution(a) Explain the meaning of the term mutual inductance. Consider two concentric circular coils, one radius r1 and the other of radius r2(r1<r2) placed coaxially with centres coinciding with each other. Obtain the expression for the mutual inductance of the arrangement.
(b) A rectangular coil of area A, having number of turns N is rotated at 'f' revoluation per second in a uniform magnetic field B, the field being perpendicular to the coil. Prove that maximum emf induced in the coil is 2πfNBA.
View SolutionTwo concentric circular coils of radius r and R are placed coaxially with centres coinciding If R>>r then calculate the mutual inductance the coils.
View SolutionTwo concentric circular coils of radius r and R are placed coaxially with centres coinciding If R>>r then calculate the mutual inductance the coils.
View SolutionTwo circular loops of radius r and R (R>>r) are placed coaxially with their centres coinciding. What will be the mutual inductance for the pair? If one of the coils is rotated through 90∘ angle, then what will be the new mutual inductance?
View SolutionTwo concentric co - planar circular loops of radius R and r(<<R) are placed as shown in the figure. The mutual inductance of the system will be

View Solution
