Obtain an expression for the position vector of centre of mass of a system of n particles in one dimension. Solution in Gujrati
According to as shown in figure. Let the distances of the two particles be x1andx2 respectively from origin O. Let m1andm2 be respectively the masses of the two particles on X-axis.
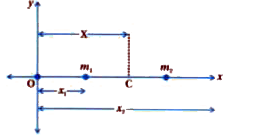
The centre of mass of the system is that point C which is at a distance X from O, then
X=m1x1+m2x2m1+m2 [X is denoted by rcm also]
where X is the mass-weighted mean of x1andx2. If the two particles have the same mass m1=m2=m, then
X=mx1+mx2m+m=x1+x22
Hence, for two particles of equal mass the centre of mass lies exactly midway between them.
Similarly, n particles of masses m1,m2,m3,...,mn their respectively, distances x1,x2,x3,...,xn from origin on X-axis then centre of mass of system of particles is given by,
X=m1x1+m2x2+m3x3+...mnxnm1+m2+m3+...mn
=ΣmixiΣmi
But Σmi=m1+m2+m3,...,mn
Σ=m = total mass of system
∴ΣmixiM (where i=1,2,3,...,n)
Topper's Solved these Questions
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - KUMAR PRAKASHANCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - SECTION-A HOTS
3 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - KUMAR PRAKASHANCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - SECTION-A (TRY YOURSELF (VSQs))
94 Videos
- QUESTIONS ASKED IN JEE - 2020 BOOK - KUMAR PRAKASHANCHAPTER - QUESTIONS ASKED IN JEE - 2020 EXERCISE - Question
16 Videos
- THERMAL PROPERTIES OF MATTERBOOK - KUMAR PRAKASHANCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Question Paper (Section - D) (Answer following in brief :) Each carry 4 marks
1 Videos
Similar Questions
What is torque? Explain the torque acting on a particle.
View SolutionWhat is a rigid body ? Explain the differences between rigid body and solid body.
View SolutionA non-isotropic solid metal cube has coefficient of linear expansion as 5×10−5/∘C along the x-axis and 5×10−6/∘C along y-axis and z-axis. If the coefficient of volumetric expansion of the solid is n×10−6/∘C then the value of n is....
View SolutionIn an experiment on the specific heat of a metal, a 0.20 kg block of the metal at 150∘C is dropped in a copper calorimeter (of water equivalent 0.025 kg) containing 150 cm3 of water at 27∘C. The final temperature is 40∘C. Compute the specific heat of the metal. If heat losses to the surroundings are not negligible, is your answer greater or smaller than the actual value for specific heat of the metal ?
View SolutionObtain an expression for the position vector of centre of mass of a two particle system.
View SolutionObtain an expression for the position vector of centre of mass of a system of n particles.
View SolutionStatement-1 : The centre of mass of a system of n particles is the weighted average of the position vector of the n particles making up the system . Statement-2 : The position of the centre of mass of a system is independent of coordinate system
View SolutionDerive an expression for the position vector of the center of mass of particle system.
View SolutionDerive an expression for the position vector of the center of mass of particle system.
View SolutionGive the expression for the centre of mass of a system of particles along any one axis.
View SolutionWhat is centre of mass of a body ? Obtain an expression for the positive vector of a centre of mass of two particle system.
View SolutionPosition vector of the centre of mass of a system of N particles of total mass M is
View SolutionWrite an expression for the position vector of the centre of mass of n-particle system. Also write the equations of motion which govern the motion of the centre of mass
View SolutionThe position vector of the centre of mass of a system of particles is the _________ of the position vectors of the particles, each particle making a contribution proportional to its _________
View SolutionWrite an expression for the velocity of the centre of mass of a system of particles.
View Solution
