A uniform plank of mass m, free to move in the horizontal directions, is placed on the top of a solid cylinder of mass 2m and radius R. the plank is attached to a fixed wall with the help of a light spring of force constant k. the is slightly displaced towards spring and released, there is no slipping anywhere. For any displacement x, amplitude x0 and velocity v of the plank, match the columns :
A) Restoring force in the plank P)12kx20B) Energy of oscillations of the system Q)KxC) Acceleration of the plank R)7.8mv2+12kx2D) Angular frequencyS)4kx7mT)√4kx7m
The correct Answer is:A-Q; B - PR ; C-S ; D-T
Topper's Solved these Questions
- SIMPLE HARMONIC MOTION BOOK - AAKASH SERIESCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - PRACTICE SHEET (EXERCISE - IV)(LEVEL - II)(STRIGHT OBJECTIVE TYPE QUESTIONS)
4 Videos
- SIMPLE HARMONIC MOTION BOOK - AAKASH SERIESCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - PRACTICE SHEET (EXERCISE - V)(LEVEL - II)(STRAIGHT OBJECTIVE TYPE QUESTIONS)
12 Videos
- SIMPLE HARMONIC MOTION BOOK - AAKASH SERIESCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - PRACTICE SHEET (EXERCISE - III)(LEVEL - II)(MORE THAN ONE CORRECT ANSWER TYPE QUESTIONS)
3 Videos
- ROTATIONAL MECHANICSBOOK - AAKASH SERIESCHAPTER - ROTATIONAL MECHANICSEXERCISE - Questions for Descriptive Answers
20 Videos
- SURFACE TENSIONBOOK - AAKASH SERIESCHAPTER - SURFACE TENSIONEXERCISE - ADDITIONAL PRACTICE EXERCISE (PRACTICE SHEET (ADVANCED) INTEGER TYPE QUESTIONS )
8 Videos
Similar Questions
A uniform plank of mass m, free to move in the horizontal direction only , is placed at the top of a solid cylinder of mass 2m and radius R. The plank is attached to a fixed wall by mean of a light spring constant k. There is no slipping between the cylinder and the planck , and between the cylinder and the ground. Find the time period of small oscillation of the system.
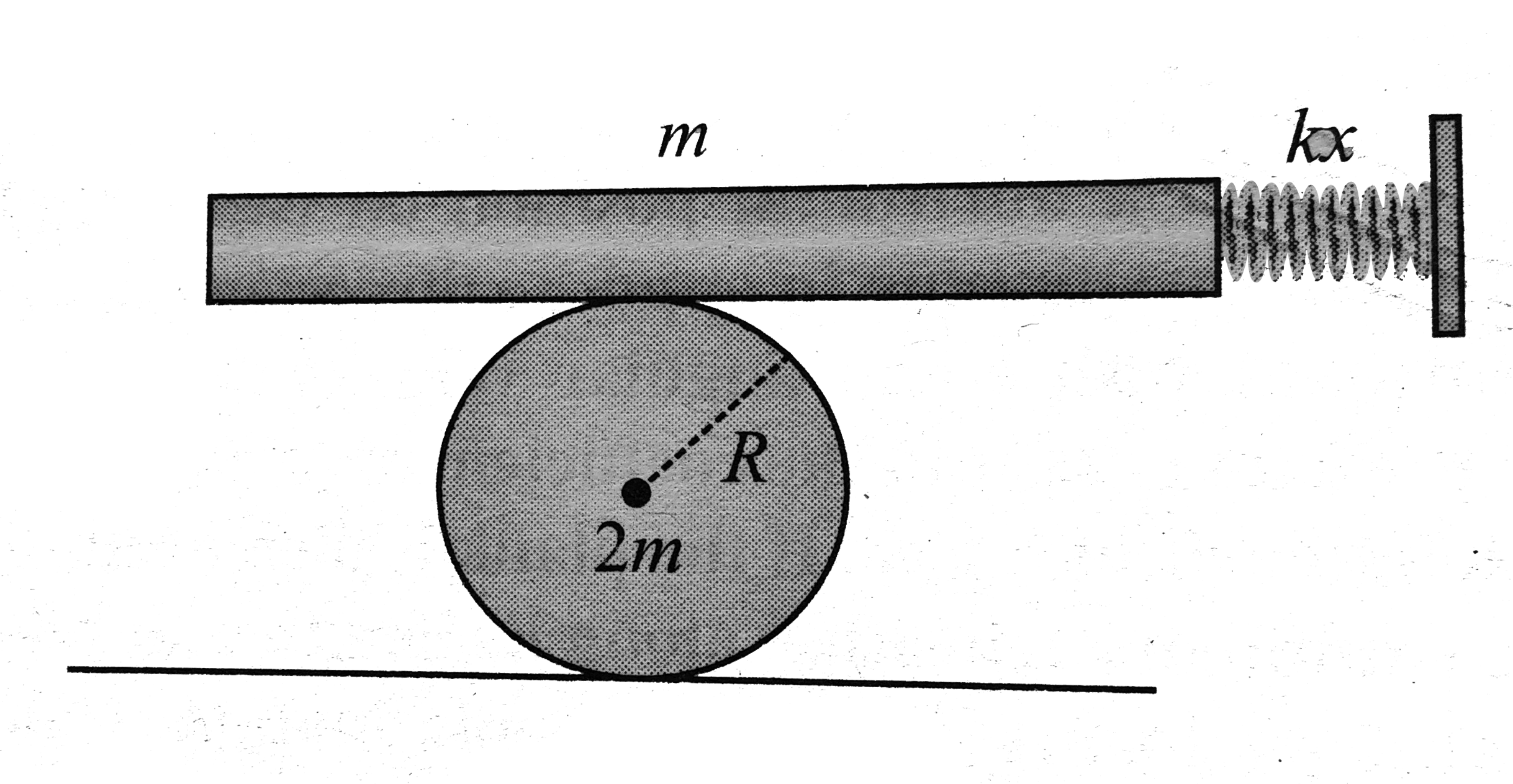
View SolutionA uniform plank of mass m, free to move in the horizontal direction only , is placed at the top of a solid cylinder of mass 2m and radius R. The plank is attached to a fixed wall by mean of a light spring constant k. There is no slipping between the cylinder and the plank , and between the cylinder and the ground. Find the time period of small oscillation of the system.

View Solution
Knowledge Check
Three springs of each force constant k are connected as shown figure. Point mass m is slightly displaced to compress A and released. Time period of oscillation is
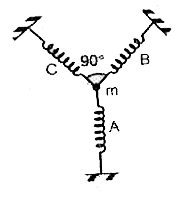 A2π√m2kB2π√m3kC2π√mkD2π√mk+√2(k+1)
A2π√m2kB2π√m3kC2π√mkD2π√mk+√2(k+1)
A block of mass m is attached to two unstretched springs of spring constant k, each as shown. The block is displaced towards right through a distance x and is released The speed of the block as it passes through the mean position will beAx√m2kBx√2kmCxmkDx2km
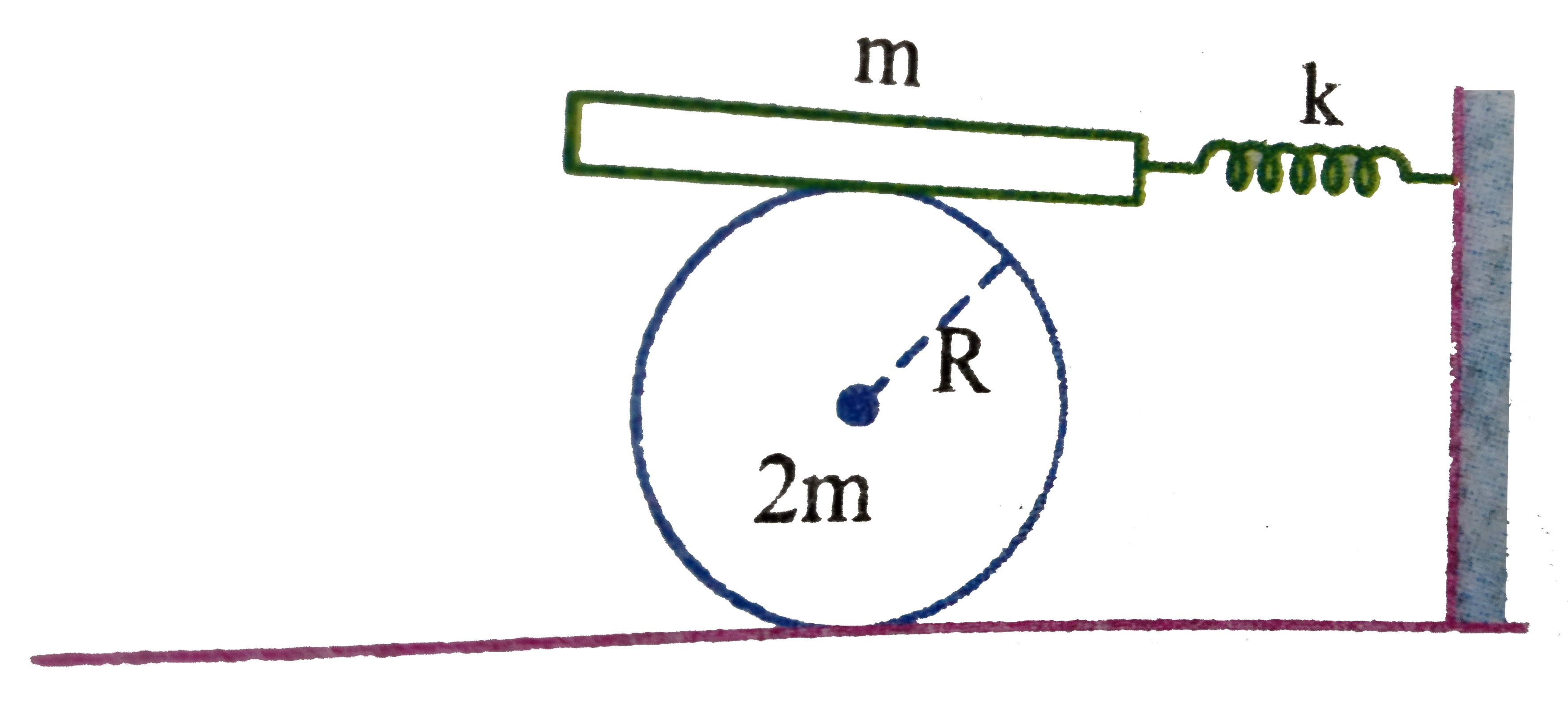
A uniform plank of mass m=1kg, free to move in the horizontal direction only, is placed at the top of a solid cylinder of mass 2m and radius R. The plank is attched to a fixed wall by means of light spring of spring constant k=7N/m2. There is no slipping between the cylinder and the plank, and between the cylinder and the ground. the angular frequency of small oscillations of the system is
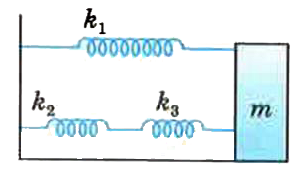
View SolutionThe figure shows an arrangement of mass m with three springs of different springs constant. When m is slightly displaced and then released, find the frequency of its motion.
View SolutionA solid cylinder of mass M and radius 2R is rolled up on an incline with the help of a plank of mass 2M as shown in the figure. A constant force F is acting on the plank parallel to the incline. There is no slipping at any of the contact. The friction force between the plank and cylinder is given by:

View SolutionA small solid cylinder of mass M attached to horizontal massless spring can roll without slipping along a horizontal surface. Show that if the cylinder is displaced slightly and released, it executes S.H.M. Also find its time period.
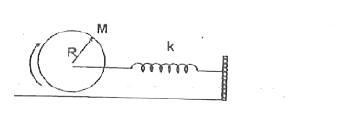
View SolutionA solid cylinder attached to horizontal massless spring can roll without slipping along a horizontal surface. Find time period of oscillation.
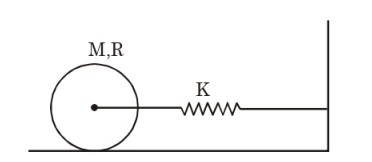
View SolutionA solid sphere of mass M and Radius R is attached to a massless spring of force constant k as shown in the figure. The cylinder is pulled towards right slightly and released so that it executes simple harmonic motion of time period. If the cylinder rolls on the horizontal surface without slipping, calculate its time period of oscillation.

View Solution
