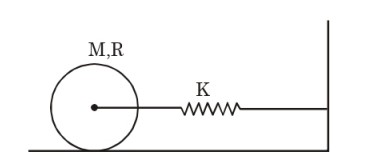
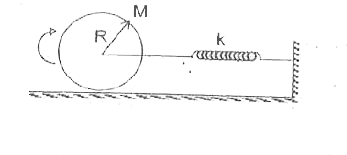
A solid cylinder attached to horizontal massless spring can roll without slipping along a horizontal surface. Find time period of oscillation.

A

$2 π \sqrt{\frac{M}{2 k}}$

B

$π \sqrt{\frac{3 M}{2 k}}$

C

$π \sqrt{\frac{2 M}{3 k}}$

D

$2 π \sqrt{\frac{3 M}{2 k}}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:D

At any instant of rolling the cylinder has rotational and translation kinetic energy
$K_{rot} = \frac{1}{2} l ω^{2} = \frac{1}{2} [\frac{1}{2} M R^{2}] [\frac{v^{2}}{R^{2}}] = \frac{1}{4} M v^{2}$
$K_{trans} = \frac{1}{2} M v^{2}$
$U_{(potential)} = \frac{1}{2} k x^{2}$
$\Rightarrow$ Total energy $E = K_{rot} + K_{trans} + U$

$\Rightarrow E = \frac{3}{4} M v^{2} + \frac{1}{2} k x^{2}$
Here $(\frac{d E}{d t}) - \frac{3}{4} M (2 v) \frac{d V}{d t} + \frac{1}{2} k 2 x (\frac{d x}{d t}) = 0$
or, $(\frac{d v}{d t}) = - (\frac{2 k}{3 M}) x$
Hence $α = - ω^{2} x$
Therefore the motion is simple harmonic
$ω = \sqrt{\frac{2 k}{3 M}}$
$\Rightarrow T = 2 π \sqrt{\frac{3 M}{2 k}}$

Updated on:21/07/2023

|

Class 12 PHYSICS SIMPLE HARMONIC MOTION

Similar Questions

Recommended Questions

Home
Ask Doubt
Profile