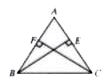
ABC is an isosceles triangle in which altitudes BE and CF are drawn to equal sides AC and AB respectively (see Fig. 7.31). Show that these altitudes are equal.
The correct Answer is:BE
Step by step video solution for ABC is an isosceles triangle in which altitudes BE and CF are drawn to equal sides AC and AB respectively (see Fig. 7.31). Show that these altitudes are equal. by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- TRIANGLESBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - TRIANGLESEXERCISE - EXERCISE 7.3
5 Videos
- TRIANGLESBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - TRIANGLESEXERCISE - EXERCISE 7.4
6 Videos
- TRIANGLESBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - TRIANGLESEXERCISE - SUMS TO ENRICH REMEMBER
9 Videos
- SURFACE AREAS AND VOLUMESBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - SURFACE AREAS AND VOLUMESEXERCISE - MULTIPLE CHOICE QUESTIONS
18 Videos
Similar Questions
Knowledge Check
In the adjoining figure, ABC is an isosceles triangle in which AB=AC. If E and F be the midpoints of AC and AB respectively, then
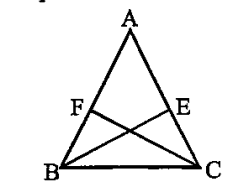 ABE=CFB∠BFC=∠CEBCBF=CEDAll of these
ABE=CFB∠BFC=∠CEBCBF=CEDAll of theseIn the adjoining figure, ABC is an isosceles triangle in which AB = AC. If E and F be the midpoints of AC and AB respectively, then
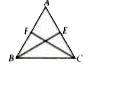 ABE = CFB∠BFC=∠CEBCBF = CEDAll of these
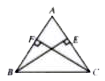
ABE = CFB∠BFC=∠CEBCBF = CEDAll of theseABC is an isosceles triangle in which altitudes BE and CF are drawn to equal sides AC and AB respectively (see Fig. 7.31). Show that these altitudes are equal.
A∠B=∠CB∠BAE=∠FACC∠AFC=∠AEBDBE = CF
ABC is a triangle in which altitude BE and CF drawn on AC and AB respectively are equal. Prove that ΔBEC≅ΔCFB
View SolutionABC is a triangle in which altitudes BE and CF to sides AC and AB are equal (see figure). Show that
AB=AC, i.e., ABC is an isosceles triangle.
View SolutionABC is a triangle in which altitudes BE and CF to sides AC and AB are equal (see Fig. 7.32). Show that
(i) ΔABE≅ΔACF
(ii) AB = AC, i.e., ABC is an isosceles triangle.
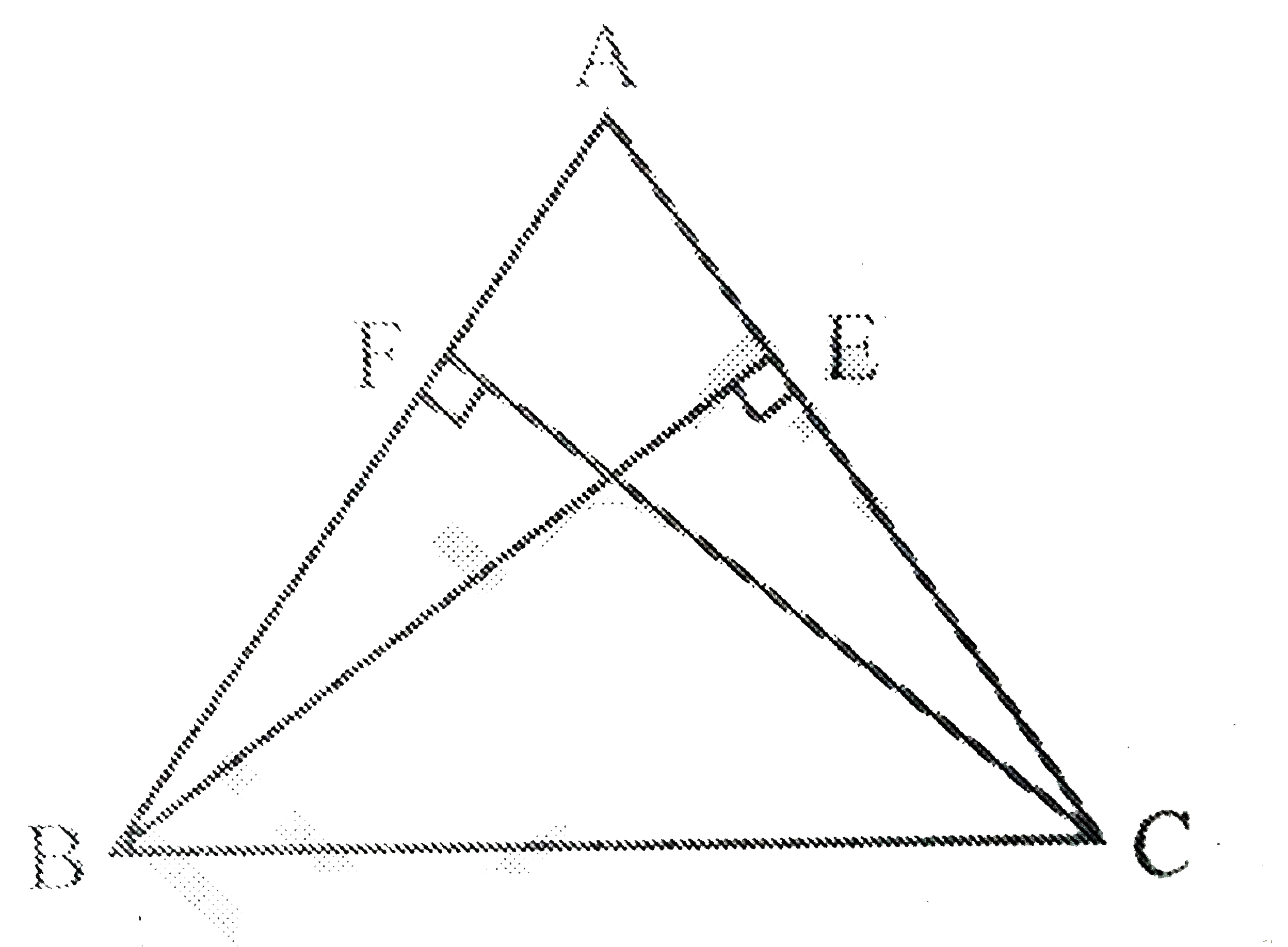
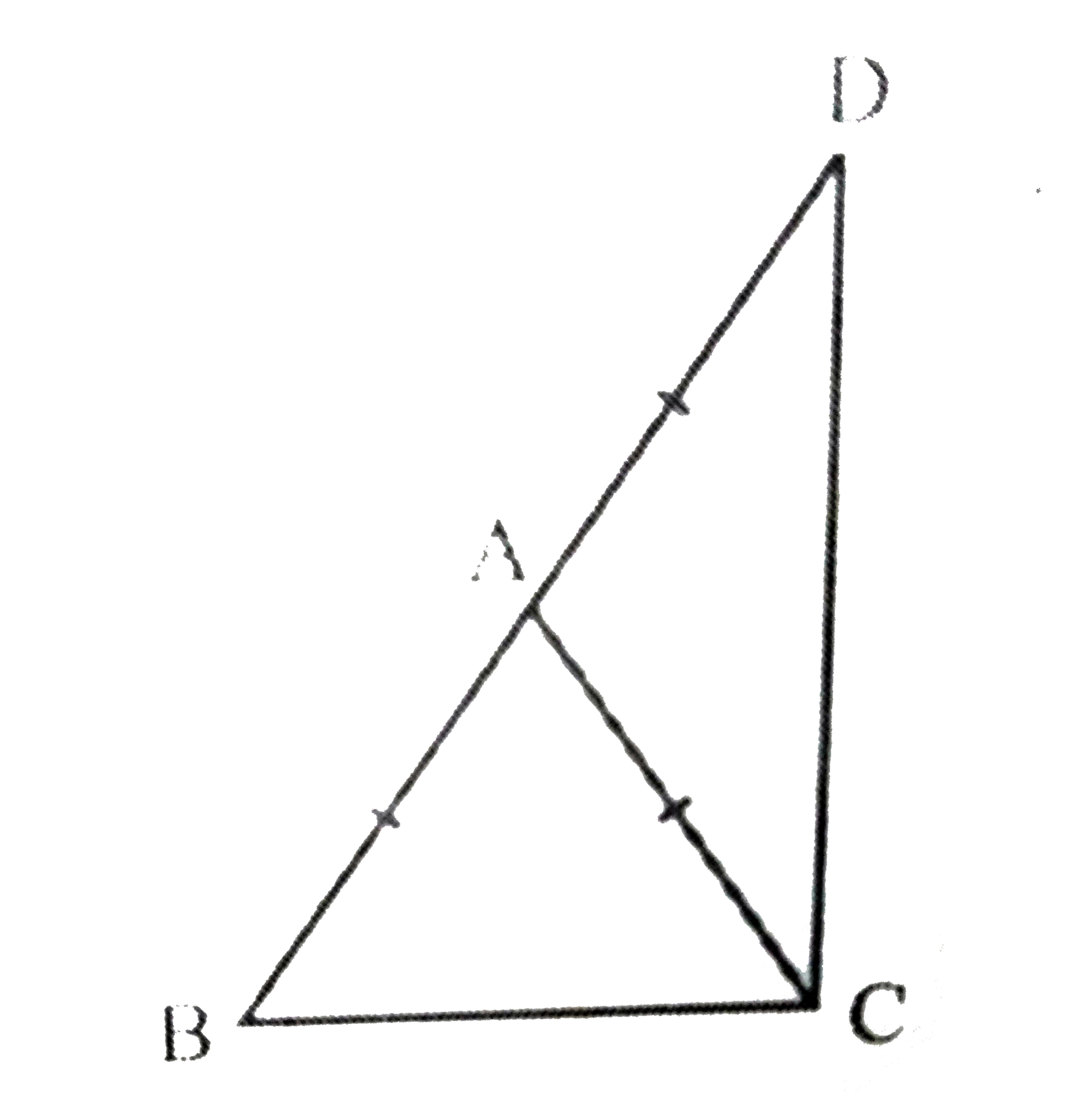
View SolutionΔABC is an isosceles triangle in which AB=AC. Side BA is produced to D such that AD=AB (see Fig. 7.34). Show that ∠BCD is a right angle.
View SolutionAD is an altitude of an isosceles triangle ABC in which AB = AC. Show that
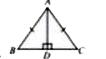
AD bisects BC
View Solution