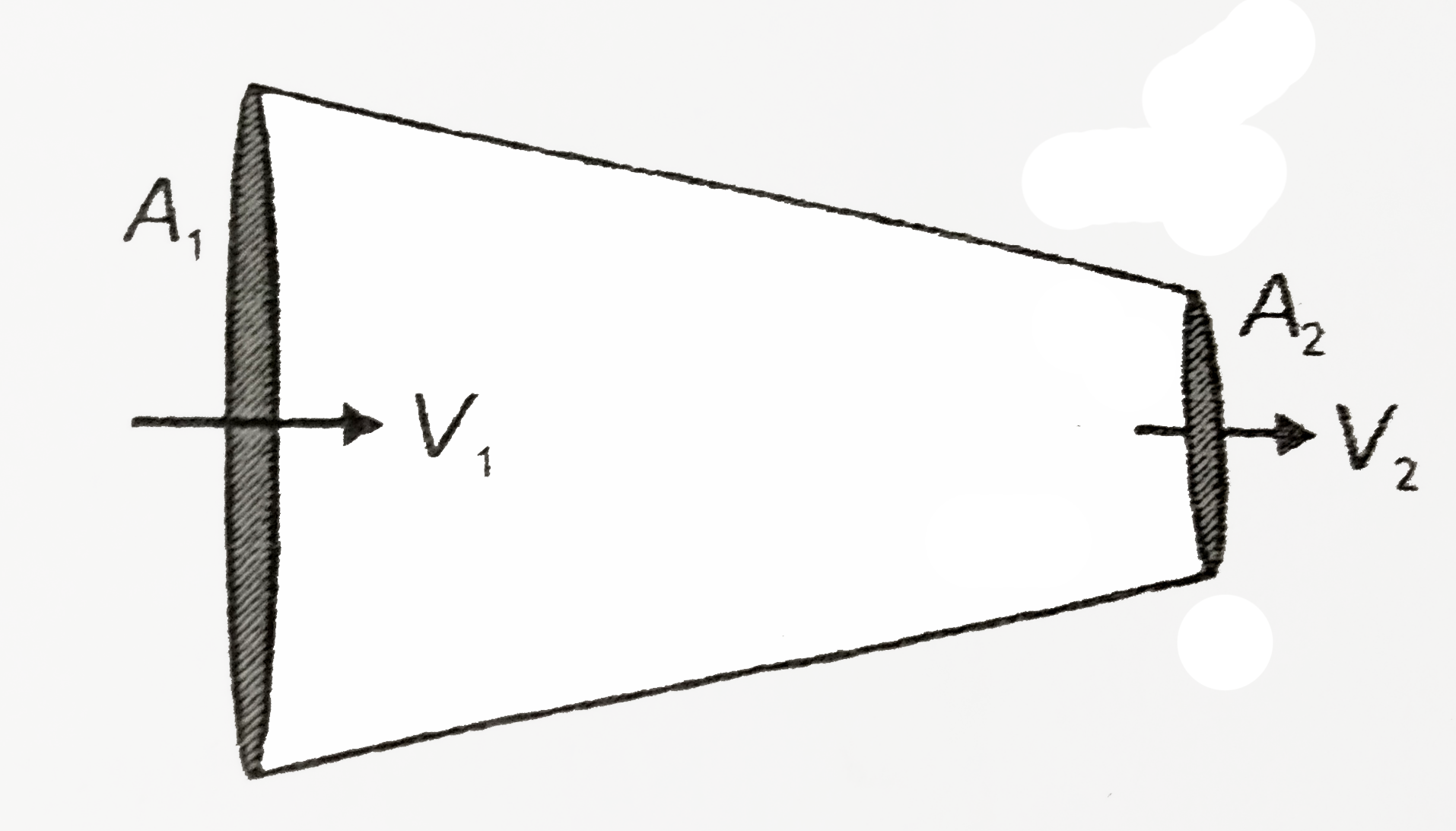
Calculate rate of flow of glycerin of density 1.25×103kg/m3 through the conical section of a horizontal pipe, if the radii of it ends are 0.1 m and 0.04 m and pressure drop across its length is 10N/m2.
According to continuity equation.
V2V1=A1A2=r21r22=(0.1)2(0.04)2=254
and according to Bernoull.s equation for a horizontal tube P1+12ρV21=P2+12ρV22
V22−V21=2(P1−P2)ρ
=2×(10N/m2)(1.25×103kg/m3)
=16×10−3m2/s2
but V2=254V1=6.25V1
[(6.25)2−12]V21=16×10−3m−2/s2
or V1≈0.0205m/s
the rate of volume flow =A1V1=π(0.1)2×(0.02)
=6.28×10−4m3/s
And the rate of mass flow is dmdt=ρAV
=(1.25×103kg/m3)×(6.28×10−4m3/s)
=0.785kg/s
Similar Questions
Calculate the rate of flow of glycerine of density 1.25×103kg/m3 through the conical section of a pipe if the radii of its ends are 0.1m and 0.04 m and the pressure drop across its lengths is 10N/m2.
View SolutionCalculate the rate of flow of glycerine of density 1.25×103kgm−3 through the conical section of a pipe, if the radii of its ends are0.1 m and 0.04 m and the pressure drop across its length is 10Nm−2.
View Solution
Knowledge Check
Two metal spheres are falling through a liquid of density 2×103kg/m3 with the same uniform speed. The material density of sphere 1 and sphere 2 are 8×103kg/m3 and 11×103kg/m3 respectively. The ratio of their radii is :-
A118B√118C32D√32A drop of radius 2×10−5 and density 1.2×103kg/m3 falls through air. The viscosity of air is 1.8×10−5Ns/m2. Neglecting buoyancy due to air, the terminal speed of the drop is
A2.8cm/sB3.8cm/sC4.8cm/sD5.8cm/s
Calculate the rate of flow of glycerine of density 1.25×103kgm−3 through the conical section of a pipe, if the radii of its ends are0.1 m and 0.04 m and the pressure drop across its length is 10Nm−2.
View SolutionCalculate the rate of flow of glycerine of density. 1.25×103kg/m3 through the conical section of a pipe. If the radii of its ends are 1.0m and 0.04m and the pressure drop across its length is 10N/m2.
View SolutionCalculate the rate of flow of glycerine of density 1.20 ×103kg/m3 through the conical section of a pipe. If the radii of its ends are 0.1 m and 0.02 m and the pressure drop across the length is 10 Nm2.
View SolutionCalculate the rate of flow of glycerine of density 1.20 ×103kg/m3 through the conical section of a pipe. If the radii of its ends are 0.1 m and 0.02 m and the pressure drop across the length is 10 Nm2.

View SolutionTwo metal spheres are falling through a liquid of density 2×103kg/m3 with the same uniform speed. The material density of sphere 1 and sphere 2 are 8×103kg/m3 and 11×103kg/m3 respectively. The ratio of their radii is :-
View SolutionCalculate the rate of flow (volume per second) of a liquid through a capillary tube of diameter 0.20×10−3m and length 1m,η=3.00×10−5Nm−2s and pressure gradient = 10 atm.
View Solution
