P is a point at a distance r from the centre of solid sphere of radius a. The gravitational potential at P is V. IF V is plotted as a function of r, which is the correct curve ?
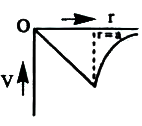
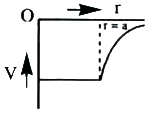
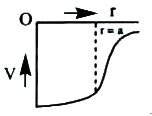
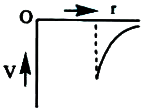
The correct Answer is:C
Topper's Solved these Questions
- GRAVITATIONALBOOK - AAKASH SERIESCHAPTER - GRAVITATIONALEXERCISE - EXERCISE -1B
46 Videos
- GRAVITATIONALBOOK - AAKASH SERIESCHAPTER - GRAVITATIONALEXERCISE - EXERCISE-2
146 Videos
- GRAVITATIONALBOOK - AAKASH SERIESCHAPTER - GRAVITATIONALEXERCISE - EXERCISE -3
154 Videos
- GRAVITATIONBOOK - AAKASH SERIESCHAPTER - GRAVITATIONEXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL-II) PRACTICE SHEET (ADVANCED)Integer Type Questions
6 Videos
- HORIZONTAL CIRCULAR MOTIONBOOK - AAKASH SERIESCHAPTER - HORIZONTAL CIRCULAR MOTIONEXERCISE - ADDITIONAL PRACTICE EXERCISE (PRACTICE SHEET (ADVANCED) Integer Type Questions)
3 Videos
Similar Questions
A uniform solid of valume mass density ρ and radius R is shown in figure.
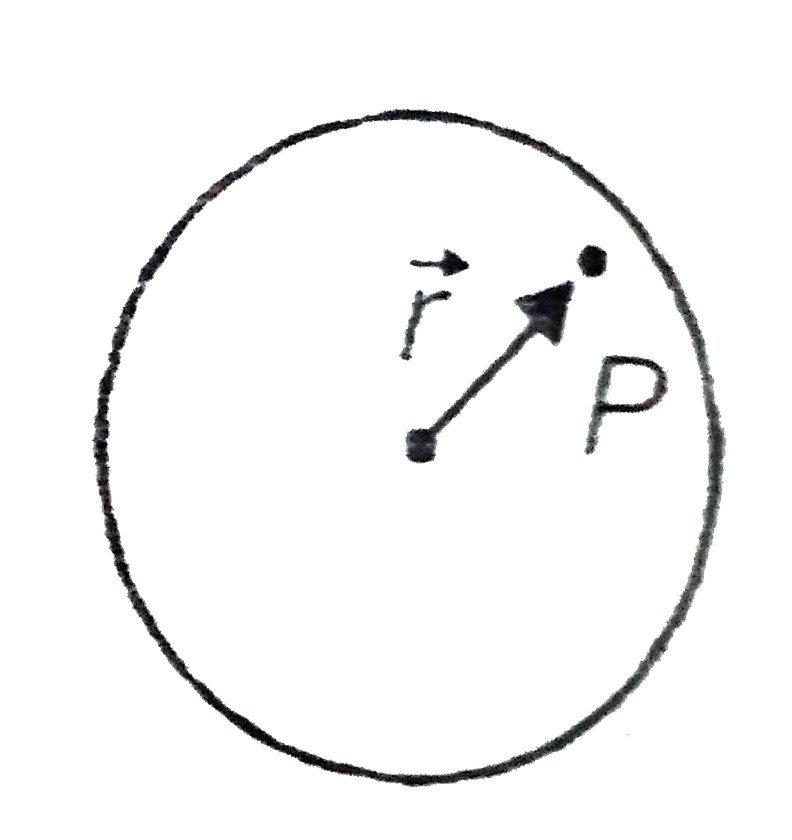
(a) Find the gravitational field at a point P inside the sphere at a distance r from the centre of the sphere. Represent the gravitational field vector →l in terms of radius vector →r of point P.
(b) Now a spherical cavity is made inside the solid sphere in such a way that the point P comes inside the cavity. The centre is at a distance a from the centre of solid sphere and point P is a distance of b from the centre of the cavity. Find the gravitational field →E at point P in vector formulationand interpret the result.
View SolutionThe distance between the centres of the Moon and the earth is D. The mass of the earth is 81 times the mass of the Moon. At what distance from the centre of the earth, the gravitational force will be zero?
View Solution
Knowledge Check
P is a point at a distance r from the centre of a solid sphere of radius a. The gravitational potential at P is V. IF V is plotted as a function of r, which is the correct curve ?
A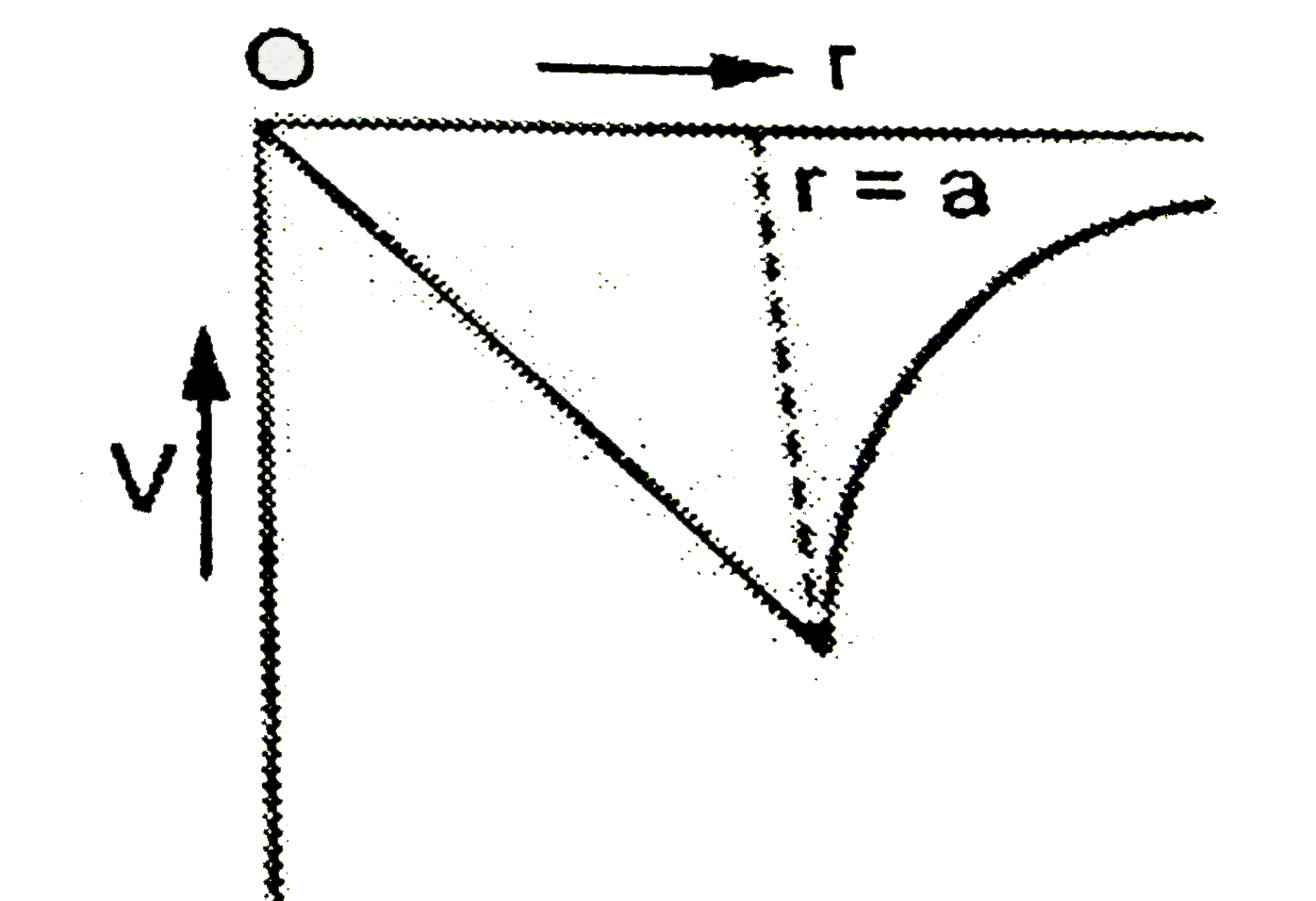 B
B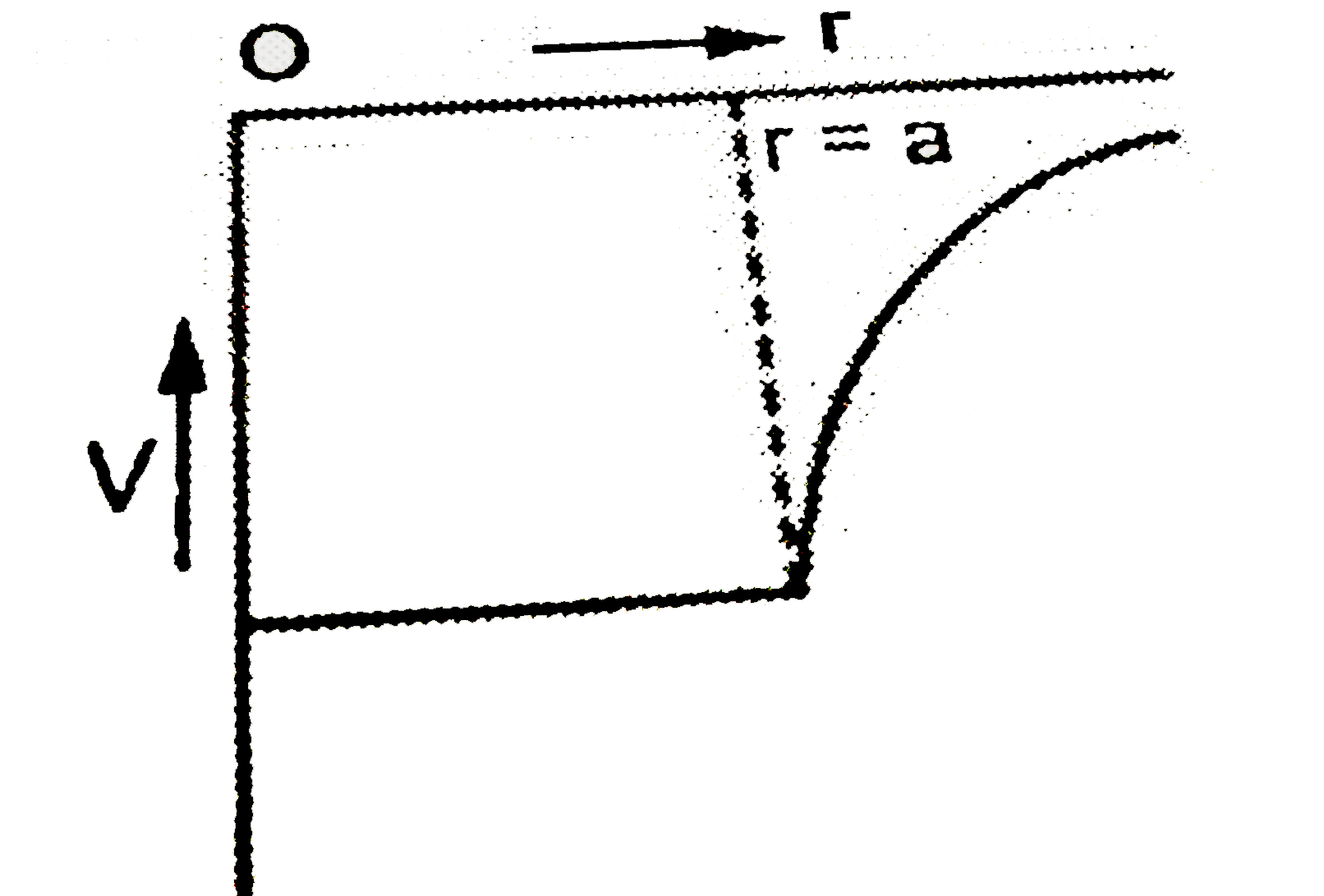 C
C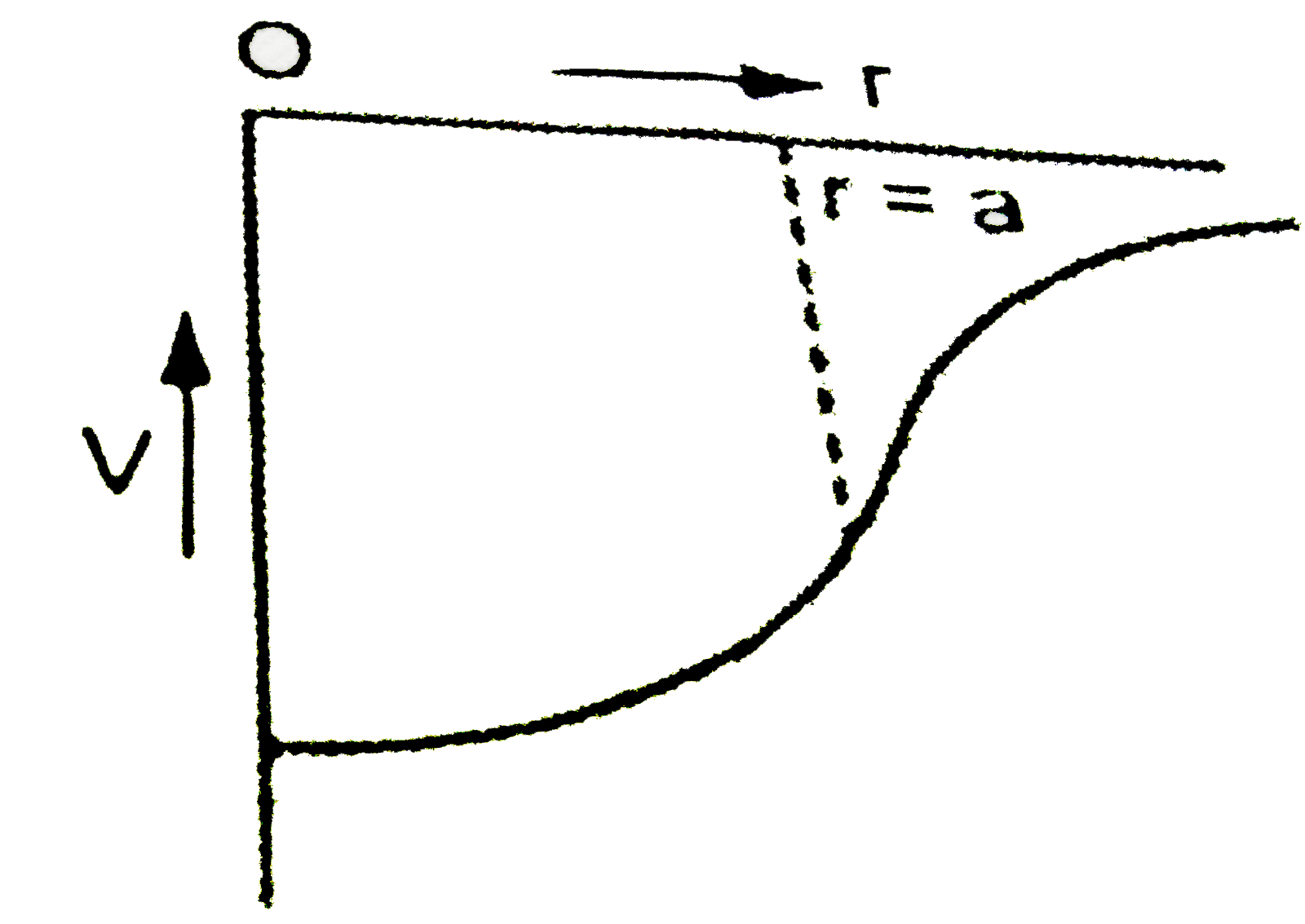 D
D
P is a point at a distance r from the centre of a spherical shell of mass M and radius a, where r<a. The gravitational potential at P is
A−GMrB−GMaC−GMra2D−GM(a−ra2)The potential at a distance R/2 from the centre of a conducting sphere of radius R will be
A0BQ8πε0RCQ4πε0RDQ2πε0R
Let V and E represent the gravitational potential and field at a distance r from the centre of a uniform solid sphere. Consider the two statements.
A. the plot of V agasinst r is discotinuous
B. The plot of E against r is discontinuous.
View SolutionThe gravitational potential at a point outside the solid sphere of radius "R" and at a distance of "r" will be :
View SolutionThere is a uniform sphere of mass M and radius R. Find the strength G and the potential varϕ of the gravitational field of this sphere as a function of the distance r from its centre (with r<R and r>R). Draw the approximate plots of the functions G(r) and φ(r).
View SolutionTwo spheres each of mass M and radius R are separated by a distance of r. The gravitational potential at the midpoint of the line joining the centres of the spheres is
View SolutionLet V and E represent the gravitational potential and field at a distance r from the centre of a uniform solid sphere. Consider the two statements.
A. the plot of V agasinst r is discotinuous
B. The plot of E against r is discontinuous.
View Solution
