A particle of mass 'm' is suspended from the ceiling through a string of length L. The particle moves in a horizontal circle of radius r. The speed of the particle is

$\frac{r g}{\sqrt{L^{2} - r^{2}}}$

$\frac{r \sqrt{g}}{{(L^{2} - r^{2})}^{\frac{1}{4}}}$

$\frac{r \sqrt{g}}{{(L^{2} - r^{2})}^{\frac{1}{2}}}$

$\frac{m g L}{{(L^{2} - r^{2})}^{\frac{1}{2}}}$

Text Solution

Verified by Experts

The correct Answer is:B

Updated on:21/07/2023

Class 11 PHYSICS RIVISION EXERCISE

Topper's Solved these Questions

RIVISION EXERCISEBOOK - AAKASH SERIESCHAPTER - RIVISION EXERCISEEXERCISE - MOTION IN A PLANE (LAMNI.S THEOREM)
6 Videos
RIVISION EXERCISEBOOK - AAKASH SERIESCHAPTER - RIVISION EXERCISEEXERCISE - FRICTION (INCLINED PLANE)
30 Videos
RAY OPTICS BOOK - AAKASH SERIESCHAPTER - RAY OPTICS EXERCISE - EXERCISE III
64 Videos
ROTATIONAL DYNAMICS BOOK - AAKASH SERIESCHAPTER - ROTATIONAL DYNAMICS EXERCISE - PRACTICE SHEET (ADVANCED) Integer Type Questions
7 Videos

Knowledge Check

A particle of mass ma is suspended from a ceiling thrugh a string of length $L$ . The prticle moves in a horizontal circle of radius $r$ . Find $(a)$ the speed of the prticle and $(b)$ . the tension in the string. Sch a system is called a conical pendulum
.
A $v = \frac{r \sqrt{g}}{{(L^{2} - r^{2})}^{\frac{1}{4}}} and T = \frac{m g L}{{(L^{2} - r^{2})}^{\frac{1}{2}}}$
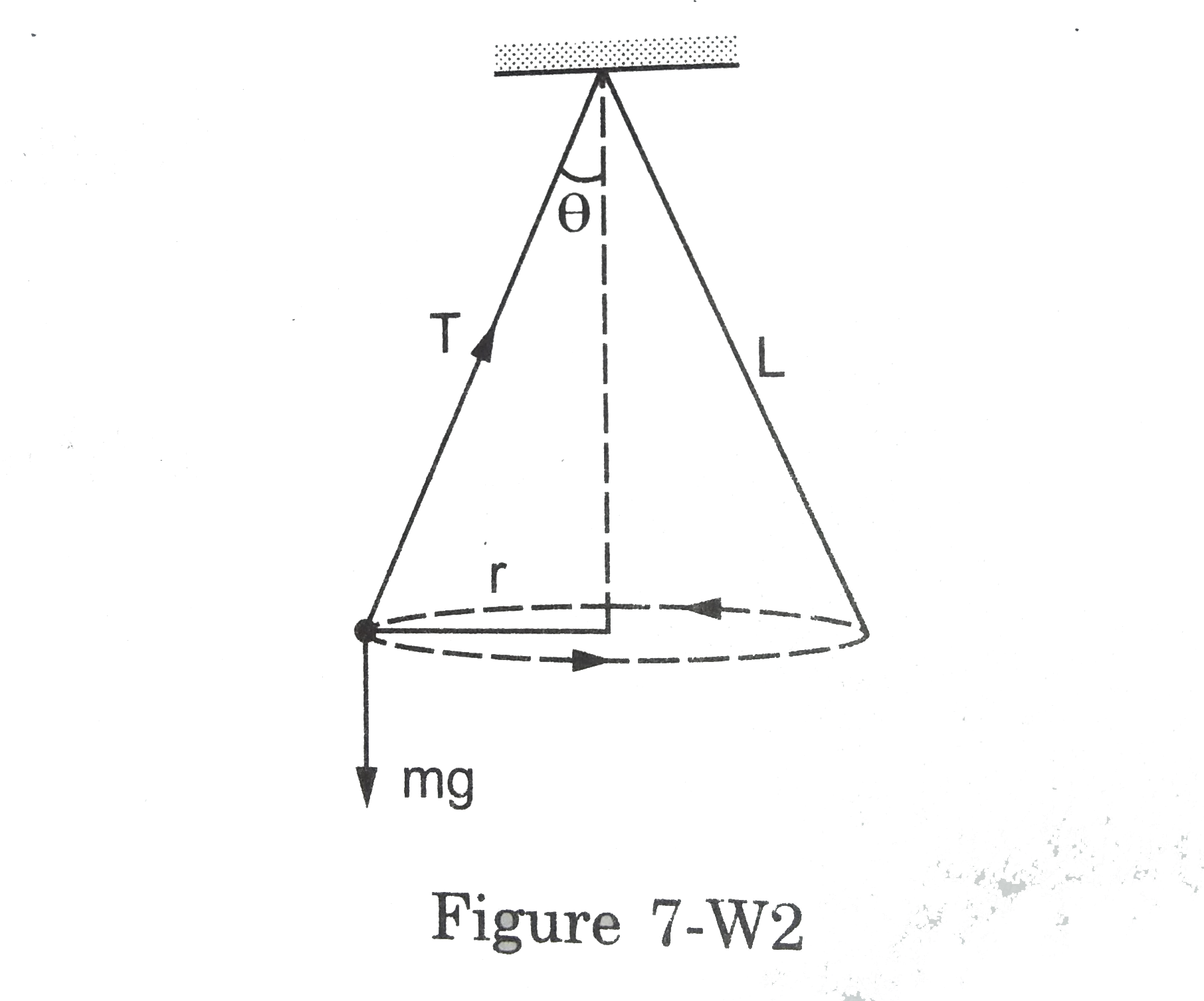
B $v = \frac{r^{2} \sqrt{g}}{{(L^{3} - r^{3})}^{\frac{1}{4}}} and T = \frac{m g L}{{(L^{2} - r^{2})}^{\frac{1}{2}}}$
C $v = \frac{r \sqrt{g}}{{(L^{2} - r^{2})}^{\frac{1}{4}}} and T = \frac{m g L^{2}}{{(L^{2} - r^{2})}^{\frac{1}{2}}}$
D $v = \frac{r \sqrt{g}}{{(L^{2} - r^{2})}^{\frac{1}{4}}} and T = \frac{m g L}{{(L^{2} - r^{2})}^{\frac{1}{4}}}$
A paricle of mass $m$ is tied to a light string of length $L$ and moving in a horizontal circle of radius $r$ with speed $v$ as shown. The forces acting on the particle are

A $m g and T$
B $m g, T, \frac{m v^{2}}{r}$ directed in wards
C $m g, T, \frac{m v^{2}}{r}$ directed outewards
D $\frac{m v^{2}}{r}$ only
A positively charged particle of charge q and mass m is suspended from a point by a string of length l. In the space a uniform horizontal electric field E exists . The particle is drawn aside so that it is projected horizontally with velocity v such that the particle starts to move along a circle with same constant speed v. Find the speed v.

A $\frac{2 q E}{m} (\frac{\sqrt{l}}{g})$
B $\frac{q E}{m} (\frac{\sqrt{l}}{g})$
C $\frac{q E}{m} (\frac{\sqrt{2 l}}{g})$
D $\frac{q E}{2 m} (\frac{\sqrt{l}}{g})$

AAKASH SERIES-RIVISION EXERCISE-FRICTION (CIRCULAR MOTION)

Home
Ask Doubt
Profile

A particle of mass 'm' is suspended from the ceiling through a string of length L. The particle moves in a horizontal circle of radius r. The speed of the particle is

The correct Answer is:B

Topper's Solved these Questions

Similar Questions

Knowledge Check

A particle of mass ma is suspended from a ceiling thrugh a string of length L. The prticle moves in a horizontal circle of radius r. Find (a) the speed of the prticle and (b). the tension in the string. Sch a system is called a conical pendulum .

A paricle of mass m is tied to a light string of length L and moving in a horizontal circle of radius r with speed v as shown. The forces acting on the particle are

AAKASH SERIES-RIVISION EXERCISE-FRICTION (CIRCULAR MOTION)

A particle of mass ma is suspended from a ceiling thrugh a string of length $L$ . The prticle moves in a horizontal circle of radius $r$ . Find $(a)$ the speed of the prticle and $(b)$ . the tension in the string. Sch a system is called a conical pendulum
.

A paricle of mass $m$ is tied to a light string of length $L$ and moving in a horizontal circle of radius $r$ with speed $v$ as shown. The forces acting on the particle are