A particle moving along straight line has velocity v=μs2 where s is the displacement. If s=s0 then which of the following graph best represent s versus t
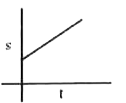
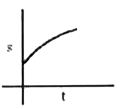
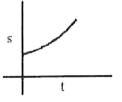
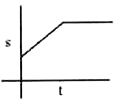
The correct Answer is:C
Topper's Solved these Questions
- RIVISION EXERCISEBOOK - AAKASH SERIESCHAPTER - RIVISION EXERCISEEXERCISE - MOTION IN A STRAIGHT LINE (VERTICAL MOTION)
58 Videos
- RIVISION EXERCISEBOOK - AAKASH SERIESCHAPTER - RIVISION EXERCISEEXERCISE - MOTION IN A PLANE (PARALLELOGRAM LAW, TRIANGLE LAW, POLYGON LAW)
14 Videos
- RIVISION EXERCISEBOOK - AAKASH SERIESCHAPTER - RIVISION EXERCISEEXERCISE - UNITS AND MEASUREMNET (SIGNIFICANT FIGURES AND ROUNDING OFF)
34 Videos
- RAY OPTICS BOOK - AAKASH SERIESCHAPTER - RAY OPTICS EXERCISE - EXERCISE III
64 Videos
- ROTATIONAL DYNAMICS BOOK - AAKASH SERIESCHAPTER - ROTATIONAL DYNAMICS EXERCISE - PRACTICE SHEET (ADVANCED) Integer Type Questions
7 Videos
Similar Questions
Knowledge Check
A particle moves along a straight line its velocity dipends on time as v=4t−t2. Then for first 5s:
AAverage velcotu is 25/3ms−1BAverage speed is 10ms−1.CAverage velcotu is 5/3ms−1DAcceleration is 4ms−2 at t=oFor a particle moving along a straight line, its velocity 'v' and displacement 's' are related as v2=cs, here c is a constant. If the displacement of the particle at t=0 is zero, its velocity after 2 sec is:
Ac2s0Bcs0Cc2s−1Dcs−1The velocity-time graph of a body moving along straight line is as follows :
The displacement of the body in 5 s is
 A5 mB2 mC4 mD3 m
A5 mB2 mC4 mD3 m
A particle is moving in a straight line and its velocity varies with its displacement as v=√4+4s m/s. Assume s=0 at t=0. find the displacement of the particle in metres at t=1s.
View SolutionA particle in moving in a straight line such that its velocity is given by v=12t−3t2, where v is in m//s and t is in seconds. If at =0, the particle is at the origin, find the velocity at t=3s.
View SolutionA particle is moving in a straight line according to the law S=t3+2t2+3t−4, where S is displacement and t is time. Find the velocity and acceleration when t=2.
View SolutionThe speed(v) of a particle moving along a straight line is given by v=(t2+3t−4 where v is in m/s and t in seconds. Find time t at which the particle will momentarily come to rest.
View SolutionThe equation of a particle moving along a straight line is s=2t3–9t2+12t, where the units of s and t are cm and s. the acceleration of the particle will be zero after
View Solution
