The natural agular frequency of a particle of mass m attached to an ideal spring of force constant K is
√Km
√mK
(Km)2
(mK)2
The correct Answer is:A
Topper's Solved these Questions
- OSCILLATIONSBOOK - AAKASH SERIESCHAPTER - OSCILLATIONSEXERCISE - Practice exercise
140 Videos
- OSCILLATIONSBOOK - AAKASH SERIESCHAPTER - OSCILLATIONSEXERCISE - EXERCISE -I Equation of S.H.M
51 Videos
- OSCILLATIONSBOOK - AAKASH SERIESCHAPTER - OSCILLATIONSEXERCISE - EXERCISE I
184 Videos
- OSCILLATIONBOOK - AAKASH SERIESCHAPTER - OSCILLATIONEXERCISE - QUESTIONS FOR DESCRIPTIVE ANSWERS
12 Videos
- PHYSICAL WORLDBOOK - AAKASH SERIESCHAPTER - PHYSICAL WORLDEXERCISE - VERY SHORT ANSWER TYPE QUESTIONS
5 Videos
Similar Questions
A block of mass m is kept on a rough horizontal surface and is attached with a massless spring of force constant k. The minimum constant force applied on the other end of the spring of lift the block is
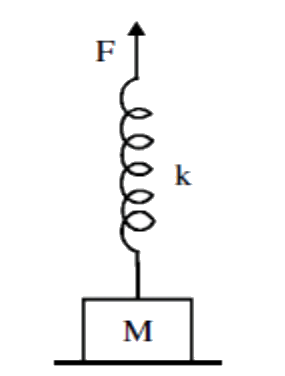
View SolutionA block of mass M is kept on a rough horizontal surface and is attached with massless spring of force constant k .The minimum constant force applied on the other end of the spring to lift the block is
View Solution
Knowledge Check
A particle of mass m is attached to three identical springs of spring constant k as shwon in figure. The time period of vertical oscillation of the particle is
 A2π√mkB2π√m2kC2π√m3kDπ√mk
A2π√mkB2π√m2kC2π√m3kDπ√mkA block is placed on a frictionless horizontal table. The mass of the block is m and springs are attached on either side with force constants K1andK2 . If the block is displaced a little and left to oscillate, then the angular frequency of oscillation will be
A(K1+K2m)1/2B[K1+K2m(K1+K2)]1/2C[K1+K2(K1−K2)m]1/2D[K1K2(K1+K2)m]1/2A particle of mass m is hanging vertically by an ideal spring of force constant K . If the mass is made to oscillate vertically, its total energy is
Amaximum at the extreme positionBmaximum at the mean positionCminimum at the mean positionDsame at all positions.
A block of mass 'm' is attached to the light spring of force constant K and released when it is in its natural length. Find amplitude of subsequent oscillations.
View SolutionA particle of mass m is hanging vertically by an ideal spring of force constant K . If the mass is made to oscillate vertically, its total energy is
View SolutionA particle of mass m is attached to three identical massless springs of spring constant k as shown in the m 135 figure. The time period of vertical oscillation of the particle is

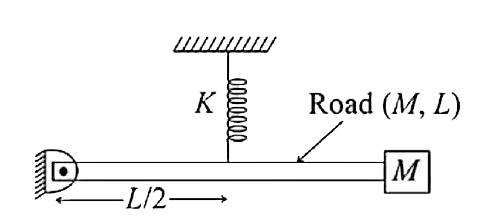
View SolutionA rod of mass 'M' and length'
L' is hinged about one end and a
particle of mass 'M' is
attached to its other end If it is
kept horizontal with the help of
a spring of spring constant 'K'
as shown in fig. find the
extension in spring :-
View SolutionThe period of oscillation of a mass M, hanging from a spring of force constant k is T. When additional mass m is attached to the spring, the period of oscillation becomes 5T/4. m/M =
View Solution
