A hoop of mass M and radius R is hung from a support fixed in a wall . Its moment of inertia about the support is
2MR2
3MR2
4MR2
6MR2
The correct Answer is:A
A hoop is a circular ring ∴I0=MR2
By theorem of parallel axes ,
I=I0+MR2=MR2+MR2=2MR2
Topper's Solved these Questions
- MOTION OF SYSTEM OF PARTICLES AND RIGID BODY BOOK - MTG GUIDECHAPTER - MOTION OF SYSTEM OF PARTICLES AND RIGID BODY EXERCISE - CHECK YOUR NEET VITALS
14 Videos
- MOTION OF SYSTEM OF PARTICLES AND RIGID BODY BOOK - MTG GUIDECHAPTER - MOTION OF SYSTEM OF PARTICLES AND RIGID BODY EXERCISE - AIPMT / NEET (MCQs)
37 Videos
- MOTION OF SYSTEM OF PARTICLES AND RIGID BODY BOOK - MTG GUIDECHAPTER - MOTION OF SYSTEM OF PARTICLES AND RIGID BODY EXERCISE - AIPMT / NEET (MCQs)
37 Videos
- LAWS OF MOTIONBOOK - MTG GUIDECHAPTER - LAWS OF MOTIONEXERCISE - AIPMT /NEET (MCQ)
24 Videos
- OSCILLATIONS AND WAVES BOOK - MTG GUIDECHAPTER - OSCILLATIONS AND WAVES EXERCISE - AIPMT / NEET MCQs
43 Videos
Similar Questions
A semicircular lamina of mass m and radius r and centre C. Its center of mass is at a distance x from C. Its moment of inertia about an axis through its center of mass and perpendicular to its plane is:
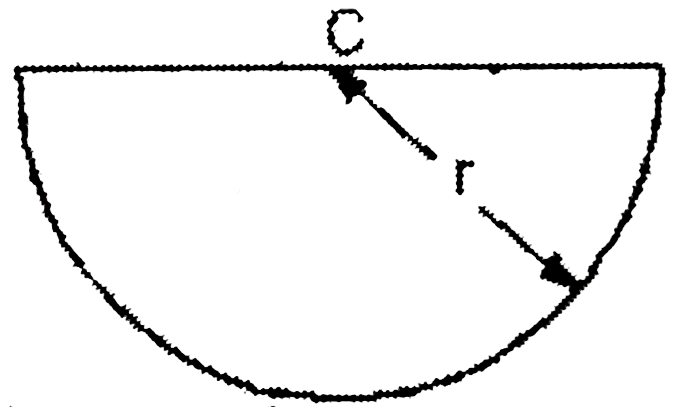
View Solution(a) Find the moment of inertia of a sphere about a tangent to the sphere, given the moment of inertia of the sphere about any of its diameters to be 2MR2/5,whereM is the mass of the sphere and R is the radius of the sphere.
(b) Given the moment of inertia of a disc of mass M and radius R about any of its diameters to be 14MR2, find the moment of inertia about an axis normal to the disc passing through a point on its edge.
View Solution
Knowledge Check
A hoop of mass 500gm & radius 10cm is placed on a nail, then the moment of inertia of the hoop, when it is rotated about the nail will be ____kgm2
A0.05B0.02C0.01D0.03The moment of inertia of a solid sphere of mass M and radius R about its diameter is I. The moment of inertia of the same sphere about a tangent parallel to the diameter is
A5 IB7 IC2.5 ID3.5 IA circular disc of mass M and radius R is suspended from a nail in the wall. The nail is fixed very near to the rim of the disc. The moment of inertia of the disc about an axis along the nail is
AMR2BMR22C32MR2DMR24
A disc of radius R has a concentric hole of radius R /2 and its mass is M. Its moment of inertia about an axis through its centre and perpendicular to its plane, is
View SolutionA disc of radius R has a concentric hole of radius R /2 and its mass is M. Its moment of inertia about an axis through its centre and perpendicular to its plane, is
View SolutionA wheel comprises a ring of radius R and mass M and three spokes of mass m each. The moment of inertia of the wheel about its axis is

View SolutionMoment of inertia of a thin circular plate of mass M, radius R about an axis passing through its diameter is I. The moment of inertia of a circular ring of mass M, radius R about an axis perpendicular to its plane and passing through its centre is
View SolutionA semicircular lamina of mass m and radius 'r' and centre C. Its center of mass is at a distance 'x' from C. Its moment of inertia about an axis through its center of mass and perpendicular to its plane is:

View Solution
