Four particles of masses m, 2m, 3m and 4m are arranged at the corners of a parallelogram with each side equal to a and one of the angle between two adjacent sides is 60∘. The parallelogram lies in the x-y plane with mass m at the origin and 4 m on the x-axis. The centre of mass of the arrangement will be located at
(√32a,0.95a)
(0.95a,√34a)
(3a4,a2)
(a2,3a4)
The correct Answer is:B
To find the center of mass of the four particles arranged at the corners of a parallelogram, we will follow these steps:
Step 1: Define the Positions of the Masses
We have four masses located at the corners of a parallelogram. The masses and their positions are as follows:
- Mass m is at the origin: (0,0)
- Mass 4m is on the x-axis: (a,0)
- Mass 2m is at an angle of 60∘ from the x-axis:
- x2=acos(60∘)=a⋅12=a2
- y2=asin(60∘)=a⋅√32=√3a2
- Mass 3m is at the opposite corner:
- x3=a+acos(60∘)=a+a2=3a2
- y3=asin(60∘)=√3a2
Step 2: List the Coordinates
Now we can summarize the coordinates:
- (x1,y1)=(0,0) for mass m
- (x2,y2)=(a2,√3a2) for mass 2m
- (x3,y3)=(3a2,√3a2) for mass 3m
- (x4,y4)=(a,0) for mass 4m
Step 3: Calculate the Center of Mass
The center of mass (Xcm,Ycm) can be calculated using the formulas:
Xcm=m1x1+m2x2+m3x3+m4x4m1+m2+m3+m4
Ycm=m1y1+m2y2+m3y3+m4y4m1+m2+m3+m4
Step 4: Substitute the Values
Substituting the values into the equations:
1. For Xcm:
Xcm=m⋅0+2m⋅a2+3m⋅3a2+4m⋅am+2m+3m+4m
=0+ma+9ma2+4ma10m
=0+ma+4.5ma+4ma10m=9.5ma10m=19a20
2. For Ycm:
Ycm=m⋅0+2m⋅√3a2+3m⋅√3a2+4m⋅010m
=0+m√3a+3√3ma210m
=0+√3a+1.5√3a10=2.5√3a10=√3a4
Final Result
Thus, the center of mass of the arrangement is located at:
(19a20,√3a4)
We have four masses located at the corners of a parallelogram. The masses and their positions are as follows:
- Mass m is at the origin: (0,0)
- Mass 4m is on the x-axis: (a,0)
- Mass 2m is at an angle of 60∘ from the x-axis:
- x2=acos(60∘)=a⋅12=a2
- y2=asin(60∘)=a⋅√32=√3a2
- Mass 3m is at the opposite corner:
- x3=a+acos(60∘)=a+a2=3a2
- y3=asin(60∘)=√3a2
Now we can summarize the coordinates:
- (x1,y1)=(0,0) for mass m
- (x2,y2)=(a2,√3a2) for mass 2m
- (x3,y3)=(3a2,√3a2) for mass 3m
- (x4,y4)=(a,0) for mass 4m
The center of mass (Xcm,Ycm) can be calculated using the formulas:
Xcm=m1x1+m2x2+m3x3+m4x4m1+m2+m3+m4
Ycm=m1y1+m2y2+m3y3+m4y4m1+m2+m3+m4
Substituting the values into the equations:
1. For Xcm:
Xcm=m⋅0+2m⋅a2+3m⋅3a2+4m⋅am+2m+3m+4m
=0+ma+9ma2+4ma10m
=0+ma+4.5ma+4ma10m=9.5ma10m=19a20
Ycm=m⋅0+2m⋅√3a2+3m⋅√3a2+4m⋅010m
=0+m√3a+3√3ma210m
=0+√3a+1.5√3a10=2.5√3a10=√3a4
Thus, the center of mass of the arrangement is located at:
(19a20,√3a4)
Topper's Solved these Questions
Similar Questions
Four particles of masses m,2m,3m,4m are placed at corners of a square of side 'a' as shown in fig. Find out coordinateds of centre of mass.
View SolutionFour particles having masses, m, 2m, 3m, and 4m are placed at the four corners of a square of edge a. Find the gravitational force acting on a particle of mass m placed at the centre.
View SolutionFour particles having masses, m, 2m, 3m, and 4m are placed at the four corners of a square of edge a. Find the gravitational force acting on a particle of mass m placed at the centre.
View SolutionFour particles having masses, m, 2m, 3m, and 4m are placed at the four corners of a square of edge a. Find the gravitational force acting on a particle of mass m placed at the center.
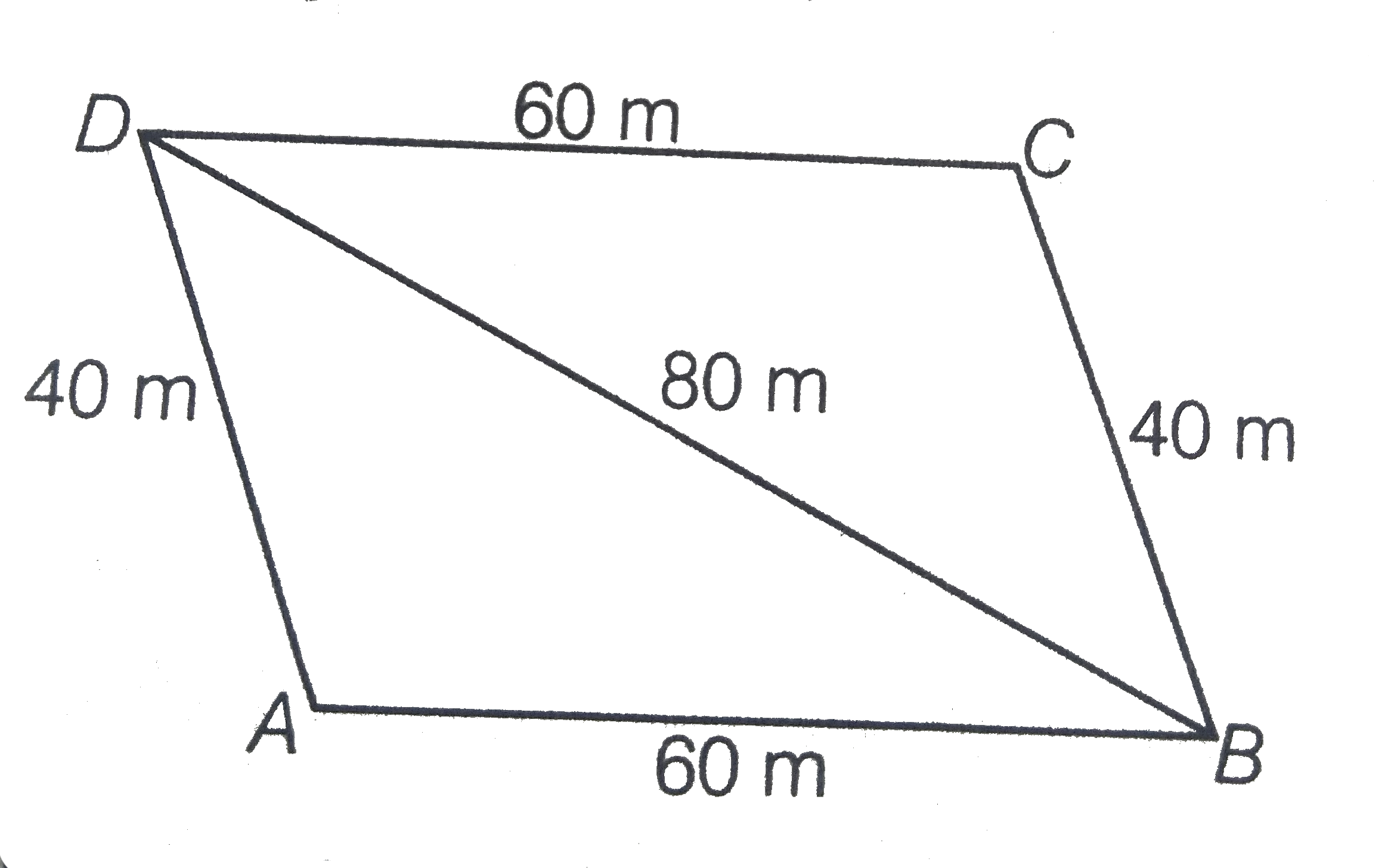
View SolutionA field in the form of a parallelogram has sides 60 m and 40 m and one of its diagonals is 80 m long. Find the area of the parallelogram.
View SolutionFour identical particles each of mass m are arranged at the corners of a square of sie a. If mass of one of th particle is doubled, the shift in the centre of mass of the system is
View SolutionFour identical particles each of mass 1 kg are arranged at the corners of a square of side length 2√2m. If one of the particles is removed, the shift in the centre of mass is
View SolutionFour identical particles each of mass 1 kg are arranged at the corners of a square of side length 2√2m. If one of the particles is removed, the shift in the centre of mass is
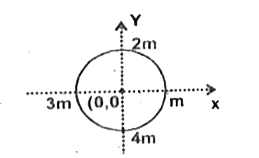
View SolutionFour particles of masses m, 2m, 3m & 4m respectively are placed on the periphery of a circle of radius R as shown in the figure then CM of the system contains the particle is at
View SolutionIf four different masses m1,m2,m3 and m4 are placed at the four corners of a square of side a, the resultant gravitational force on a mass m kept at the centre is
View Solution
