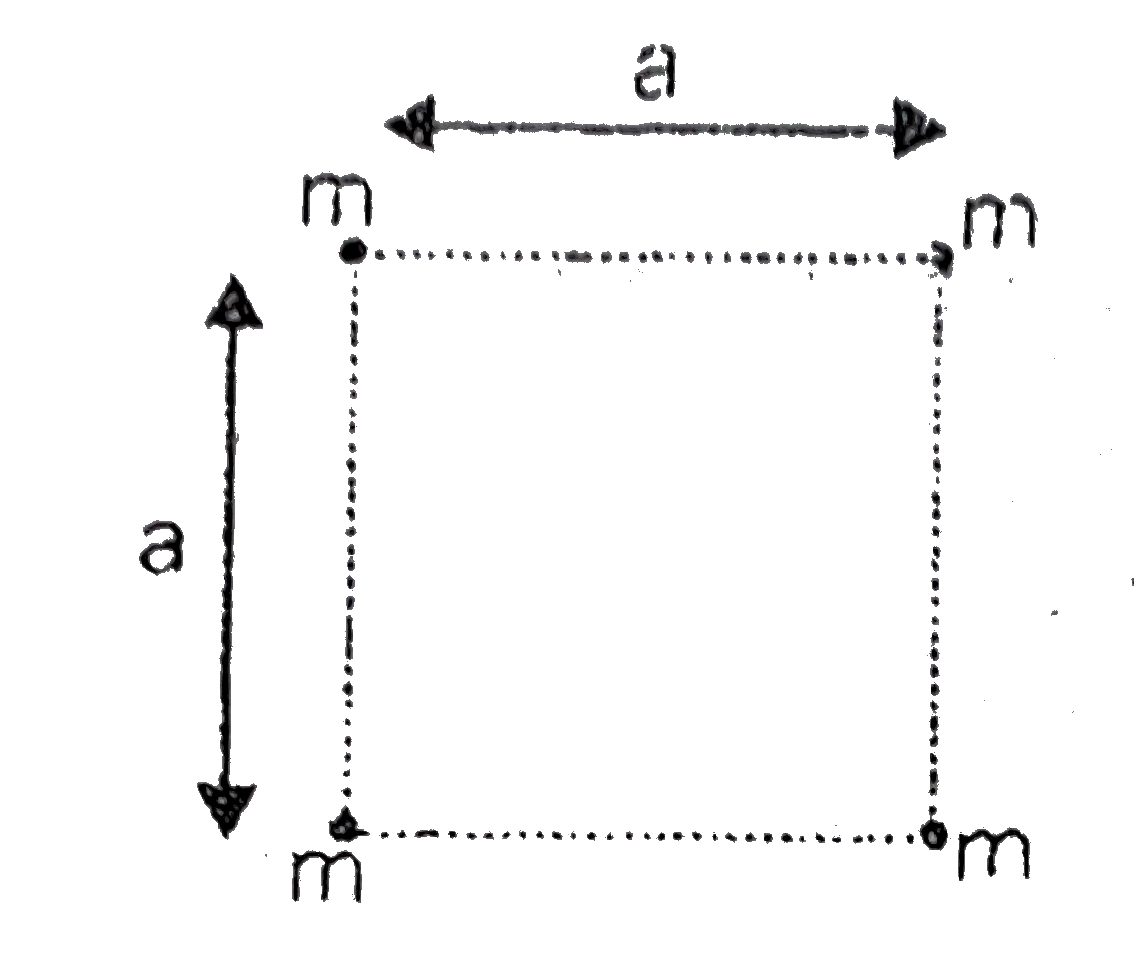
If four different masses m1,m2,m3 and m4 are placed at the four corners of a square of side a, the resultant gravitational force on a mass m kept at the centre is
The correct Answer is:Zero
To find the resultant gravitational force on a mass m placed at the center of a square with four different masses m1,m2,m3, and m4 located at the corners, we can follow these steps:
1. Identify the Setup:
- We have a square with side length a.
- The masses m1,m2,m3, and m4 are placed at the corners of the square.
- The mass m is placed at the center of the square.
2. Calculate the Distance from the Center to the Corners:
- The distance r from the center of the square to any corner can be calculated using the Pythagorean theorem.
- Since the center divides the square into two equal halves, the distance from the center to a corner is given by:
r=a√2
3. Calculate the Gravitational Force from Each Mass:
- The gravitational force F exerted by a mass mi on mass m is given by Newton's law of gravitation:
Fi=Gmimr2
- Substituting r=a√2:
Fi=Gmim(a√2)2=Gmim⋅2a2
4. Determine the Direction of Each Force:
- The forces due to m1 and m3 will act along one diagonal of the square, while the forces due to m2 and m4 will act along the other diagonal.
- The force F1 from m1 will be directed towards the center, and similarly for m3. The same applies for m2 and m4.
5. Calculate the Resultant Forces Along Each Diagonal:
- The resultant force along one diagonal (let's say from m1 and m3):
F13=F1−F3=Gmm1(a√2)2−Gmm3(a√2)2=Gma22(m1−m3)
- The resultant force along the other diagonal (from m2 and m4):
F24=F2−F4=Gmm2(a√2)2−Gmm4(a√2)2=Gma22(m2−m4)
6. Combine the Resultant Forces:
- Since F13 and F24 are perpendicular to each other, we can find the magnitude of the resultant gravitational force FR using the Pythagorean theorem:
FR=√F213+F224
- Substituting the expressions for F13 and F24:
FR=
⎷⎛⎜⎝Gma22(m1−m3)⎞⎟⎠2+⎛⎜⎝Gma22(m2−m4)⎞⎟⎠2
- Simplifying this gives:
FR=Gma22√(m1−m3)2+(m2−m4)2
Final Result:
The resultant gravitational force on mass m at the center of the square is:
FR=2Gma2√(m1−m3)2+(m2−m4)2
- We have a square with side length a.
- The masses m1,m2,m3, and m4 are placed at the corners of the square.
- The mass m is placed at the center of the square.
- The distance r from the center of the square to any corner can be calculated using the Pythagorean theorem.
- Since the center divides the square into two equal halves, the distance from the center to a corner is given by:
r=a√2
- The gravitational force F exerted by a mass mi on mass m is given by Newton's law of gravitation:
Fi=Gmimr2
- Substituting r=a√2:
Fi=Gmim(a√2)2=Gmim⋅2a2
- The forces due to m1 and m3 will act along one diagonal of the square, while the forces due to m2 and m4 will act along the other diagonal.
- The force F1 from m1 will be directed towards the center, and similarly for m3. The same applies for m2 and m4.
- The resultant force along one diagonal (let's say from m1 and m3):
F13=F1−F3=Gmm1(a√2)2−Gmm3(a√2)2=Gma22(m1−m3)
- The resultant force along the other diagonal (from m2 and m4):
F24=F2−F4=Gmm2(a√2)2−Gmm4(a√2)2=Gma22(m2−m4)
- Since F13 and F24 are perpendicular to each other, we can find the magnitude of the resultant gravitational force FR using the Pythagorean theorem:
FR=√F213+F224
- Substituting the expressions for F13 and F24:
FR=
⎷⎛⎜⎝Gma22(m1−m3)⎞⎟⎠2+⎛⎜⎝Gma22(m2−m4)⎞⎟⎠2
- Simplifying this gives:
FR=Gma22√(m1−m3)2+(m2−m4)2
The resultant gravitational force on mass m at the center of the square is:
FR=2Gma2√(m1−m3)2+(m2−m4)2
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - GRAVITATIONEXERCISE - BOX-213videos
GRAVITATION
- BOOK - ALLENCHAPTER - GRAVITATIONEXERCISE - BOX-38videos
GRAVITATION
- BOOK - ALLENCHAPTER - GRAVITATIONEXERCISE - Illustration34videos
GRAVITATION
- BOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - subjective14videos
GEOMETRICAL OPTICS
- BOOK - ALLENCHAPTER - KINEMATICS-2DEXERCISE - Exercise (O-2)46videos
KINEMATICS-2D
Similar Questions
Four particles having masses, m, 2m, 3m, and 4m are placed at the four corners of a square of edge a. Find the gravitational force acting on a particle of mass m placed at the centre.
View SolutionFour particles having masses, m, 2m, 3m, and 4m are placed at the four corners of a square of edge a. Find the gravitational force acting on a particle of mass m placed at the centre.
View SolutionFour particles having masses, m, 2m, 3m, and 4m are placed at the four corners of a square of edge a. Find the gravitational force acting on a particle of mass m placed at the center.
View SolutionFour point masses each of mass 'm' are placed on the corner of square of side 'a' Calculate magnitude of gravitational force experienced each particle
 .View Solution
.View SolutionThree masses, each equal to M, are placed at the three corners of a square of side a. the force of attraction on unit mass at the fourth corner will be
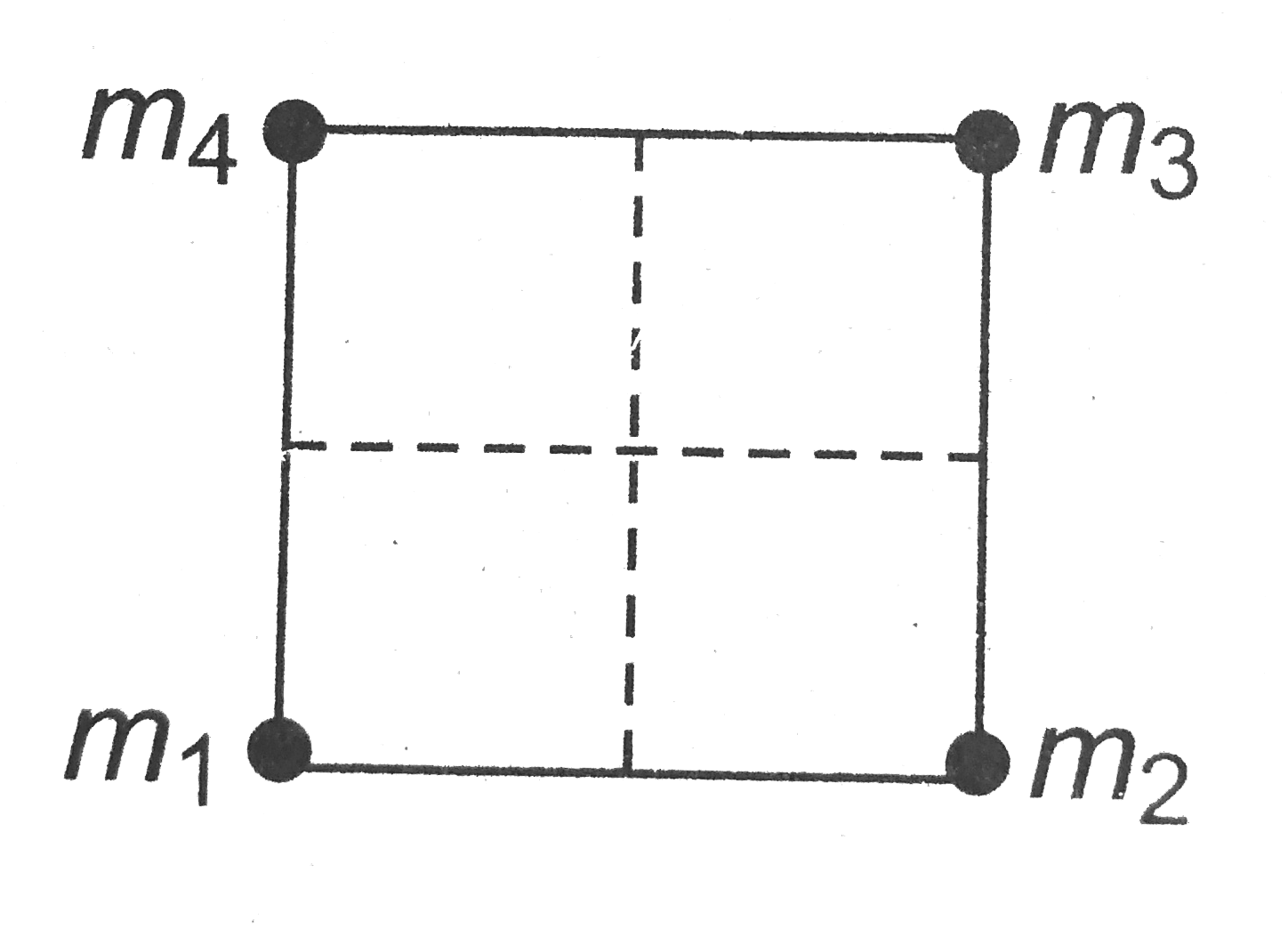
View SolutionFour paticle of masses m1=2m,m2=4m,m3=mandm4 are placed at four corners of a square. What should be the value of m4 so that the centres of mass of all the four particle are exactly at the centre of the square ?
 View Solution
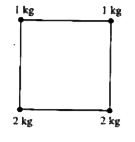
View SolutionFour point masses 1 kg, 1 kg, 2 kg and 2 kg are placed at the corners of a square of side a m as shown in Fig. Find the centre of mass of the system.
 View Solution
View SolutionFour point are placed at four comerse of a squared of side 4 m as shown. Match the following table.
 View Solution
View SolutionFour point masses are placed at the corners of a square of side 2 m as shown in the figure. Find the centre of mass of the system w.r.t. the centre of square.
 View Solution
View SolutionFour particles of masses 1kg, 2kg, 3kg and 4kg are placed at the four vertices A, B, C and D of a square of side 1m. Find the position of centre of mass of the particles.
View Solution

