Light is incident on a glass surface at polarising angle of 57.5∘ Then the angle between the incident ray and the refracted ray is
57.5∘
115∘
205∘
145∘
The correct Answer is:C
To solve the problem, we need to find the angle between the incident ray and the refracted ray when light is incident on a glass surface at a polarizing angle of 57.5 degrees.
1. Understand the Polarizing Angle: The polarizing angle (also known as Brewster's angle) is the angle of incidence at which light with a particular polarization is perfectly transmitted through a transparent dielectric surface, with no reflection.
2. Identify the Given Data:
- Polarizing angle (θ_p) = 57.5 degrees.
3. Use the Relationship Between Angles:
- At the polarizing angle, the angle between the reflected ray and the refracted ray is 90 degrees. This means that if we denote:
- θ_i = angle of incidence (57.5 degrees),
- θ_r = angle of reflection (also 57.5 degrees),
- θ_t = angle of refraction,
then we have:
θr+θt=90∘
4. Calculate the Angle of Refraction:
- Since θ_r = 57.5 degrees, we can find θ_t:
θt=90∘−θr=90∘−57.5∘=32.5∘
5. Find the Angle Between Incident Ray and Refracted Ray:
- The angle between the incident ray and the refracted ray is the sum of the angle of incidence and the angle of refraction:
Angle between incident ray and refracted ray=θi+θt=57.5∘+32.5∘=90∘
Final Answer:
The angle between the incident ray and the refracted ray is 90 degrees.
- Polarizing angle (θ_p) = 57.5 degrees.
- At the polarizing angle, the angle between the reflected ray and the refracted ray is 90 degrees. This means that if we denote:
- θ_i = angle of incidence (57.5 degrees),
- θ_r = angle of reflection (also 57.5 degrees),
- θ_t = angle of refraction,
then we have:
θr+θt=90∘
- Since θ_r = 57.5 degrees, we can find θ_t:
θt=90∘−θr=90∘−57.5∘=32.5∘
- The angle between the incident ray and the refracted ray is the sum of the angle of incidence and the angle of refraction:
Angle between incident ray and refracted ray=θi+θt=57.5∘+32.5∘=90∘
The angle between the incident ray and the refracted ray is 90 degrees.
Topper's Solved these Questions
- WAVE OPTICSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - HIGHER ORDER THINKING SKILLS
8 Videos
- WAVE OPTICSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - NCERT EXEMPLAR PROBLEMS
5 Videos
- SEMICONDUCTOR ELECTRONICS : MATERIALS , DEVICES AND SIMPLE CIRCUITS BOOK - NCERT FINGERTPS ENGLISHCHAPTER - SEMICONDUCTOR ELECTRONICS : MATERIALS , DEVICES AND SIMPLE CIRCUITS EXERCISE - Assertion And Reason
15 Videos
Similar Questions
Knowledge Check
A ray of light in incident on a glass plate at an angle of 60∘. What is the refractive index of glass if the reflected and refracted rays are perpendicular to each other?
A12B√32C32D√3
A ray of light-is incident on glass at the polarising angle ip. Find the angle between the reflected and refracted rays.
View SolutionA ray of ordinary light is travelling in air. It is incident on air glass pair at a polarising angle of 56∘. Find the angle of refraction in glass.
View SolutionIf the angle of incidence is 32∘, then what will the angle between incident ray and reflected ray?
View SolutionUnpolarized light is incident on a plane glass surface having refractive index . The angle of incidence at which reflected and refracted rays would become perpendicular to each other is :
View SolutionUnpolarized light is incident on a plane glass surface. What should be the angle of incidence so that the reflected and refracted rays are perpendicular to eachother ?
View SolutionThe diagram below shows a light ray striking and reflecting from a plane mirror AO is the incident ray and OB the reflected ray. The angle between the incident ray and the reflected ray is 120∘.
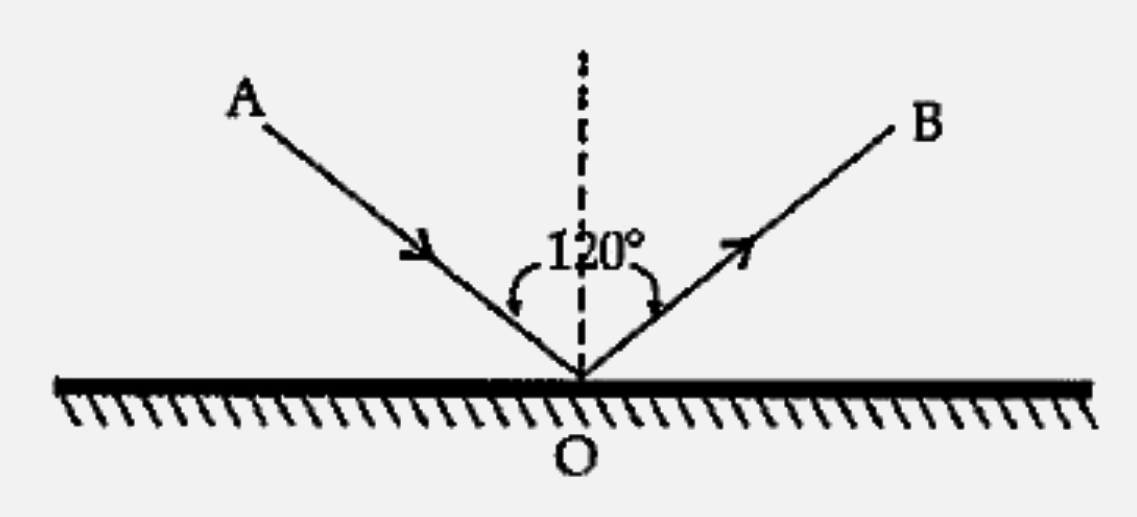
What is the value of the angle of reflection?
View SolutionA ray of light is incident at 65∘ on one face of a prism of angle of 30∘ and the emergent ray makes 35∘ with the incident ray. The refractive index of the prism is:
View Solution
