Question

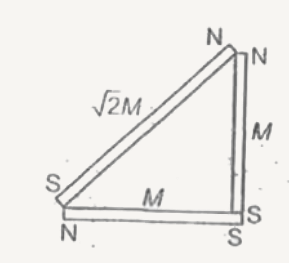
Three identical bar magnets each of magnetic moment $M$ are arranged in the form of an equilateral triangle such that at two vertices like poles are in contact. The resultant magnetic moment will be

Options

A. Zero
B. 2M
C. `sqrt(2)M`
D. `Msqrt(3)`

Answer

B

Explanation

To solve the problem of finding the resultant magnetic moment of three identical bar magnets arranged in the form of an equilateral triangle with like poles in contact, we can follow these steps:

1. Understanding the Configuration:
- We have three identical bar magnets, each with a magnetic moment \( M \).
- They are arranged in an equilateral triangle such that at two vertices, the like poles (North-North or South-South) are in contact.

2. Identifying the Magnetic Moments:
- Let's denote the magnetic moments of the three magnets as \( M_1, M_2, \) and \( M_3 \).
- For our configuration, we can assume:
- \( M_1 \) is directed upwards (North pole pointing up).
- \( M_2 \) and \( M_3 \) are directed downwards (South poles pointing down).

3. Direction of Magnetic Moments:
- The direction of the magnetic moment is from the South pole to the North pole.
- Therefore, we can represent the magnetic moments as vectors:
- \( \vec{M_1} = M \hat{j} \) (upward)
- \( \vec{M_2} = -M \left( \cos 60^\circ \hat{i} + \sin 60^\circ \hat{j} \right) \)
- \( \vec{M_3} = -M \left( \cos 60^\circ \hat{i} - \sin 60^\circ \hat{j} \right) \)

4. Calculating the Resultant of \( M_2 \) and \( M_3 \):
- Since \( M_2 \) and \( M_3 \) are at an angle of \( 60^\circ \) to each other, we can find their resultant \( \vec{M_{23}} \).
- The resultant can be calculated using the formula for the resultant of two vectors:
\( M_{23} = \sqrt{M_2^2 + M_3^2 + 2M_2M_3 \cos(60^\circ)} \)
- Since \( M_2 = M_3 = M \):
\( M_{23} = \sqrt{M^2 + M^2 + 2M^2 \cdot \frac{1}{2}} = \sqrt{3M^2} = \sqrt{3}M \)

5. Finding the Resultant Magnetic Moment:
- Now, we have \( \vec{M_1} \) and \( \vec{M_{23}} \) which are perpendicular to each other.
- The resultant magnetic moment \( \vec{M_R} \) can be calculated as:
\( M_R = \sqrt{M_1^2 + M_{23}^2} = \sqrt{M^2 + (\sqrt{3}M)^2} = \sqrt{M^2 + 3M^2} = \sqrt{4M^2} = 2M \)

6. Conclusion:
- The resultant magnetic moment of the system is \( 2M \).

Final Answer:
The resultant magnetic moment will be \( 2M \).