Assertion : For a particle, acceleration-time graph gives the velocity.
Reason : Rate of change of velocity is acceleration.
If both assertion and reason are trure and reason is the correct explanation of assertion.
If both assertion and reason are true but reason is not the correct explanations of assertion.
If assertion is true but reason is false.
If both assertion and reason is false
The correct Answer is:(b)
Step-by-Step Solution
1. Understanding the Assertion and Reason:
- Assertion: For a particle, the acceleration-time graph gives the velocity.
- Reason: The rate of change of velocity is acceleration.
2. Analyzing the Reason:
- The reason states that acceleration is defined as the rate of change of velocity with respect to time. Mathematically, this is expressed as:
a=dvdt
- This statement is true. It indicates how velocity changes over time.
3. Understanding the Acceleration-Time Graph:
- An acceleration-time graph plots acceleration (a) on the y-axis against time (t) on the x-axis.
- The area under the acceleration-time graph represents the change in velocity (Δv) over a specific time interval.
4. Relating Area Under the Graph to Velocity:
- If we consider a time interval from t1 to t2, the area under the acceleration-time graph can be calculated as:
Area=∫t2t1adt=Δv
- This means that the area under the curve gives us the change in velocity during that time interval.
5. Using the Equation of Motion:
- According to the equations of motion, we have:
v=u+at
- If we consider the initial velocity u=0, then:
v=at
- This shows that the final velocity is directly related to the acceleration and the time for which it acts.
6. Conclusion:
- The assertion that the acceleration-time graph gives velocity is correct because the area under the graph provides the change in velocity.
- The reason is also correct, but it does not directly explain why the assertion is true. Therefore, both statements are correct, but the reason is not a correct explanation of the assertion.
Final Answer:
- Both the assertion and reason are correct, but the reason is not a correct explanation of the assertion. Thus, the correct option is B.
- Assertion: For a particle, the acceleration-time graph gives the velocity.
- Reason: The rate of change of velocity is acceleration.
- The reason states that acceleration is defined as the rate of change of velocity with respect to time. Mathematically, this is expressed as:
a=dvdt
- This statement is true. It indicates how velocity changes over time.
- An acceleration-time graph plots acceleration (a) on the y-axis against time (t) on the x-axis.
- The area under the acceleration-time graph represents the change in velocity (Δv) over a specific time interval.
- If we consider a time interval from t1 to t2, the area under the acceleration-time graph can be calculated as:
Area=∫t2t1adt=Δv
- This means that the area under the curve gives us the change in velocity during that time interval.
- According to the equations of motion, we have:
v=u+at
- If we consider the initial velocity u=0, then:
v=at
- This shows that the final velocity is directly related to the acceleration and the time for which it acts.
- The assertion that the acceleration-time graph gives velocity is correct because the area under the graph provides the change in velocity.
- The reason is also correct, but it does not directly explain why the assertion is true. Therefore, both statements are correct, but the reason is not a correct explanation of the assertion.
- Both the assertion and reason are correct, but the reason is not a correct explanation of the assertion. Thus, the correct option is B.
Topper's Solved these Questions
- MOTION IN A STRAIGHT LINEBOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - Higher Order Thinking Skills
10 Videos
- MOTION IN A STRAIGHT LINEBOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - NCERT Exemplar
6 Videos
- MOTION IN A STRAIGHT LINEBOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - NCERT EXEMPLAR PROBLEMS
6 Videos
- MOTION IN A PLANE BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOTION IN A PLANE EXERCISE - Assertion And Reason
15 Videos
- OSCILLATIONS BOOK - NCERT FINGERTPS ENGLISHCHAPTER - OSCILLATIONS EXERCISE - Assertion And Reason
15 Videos
Similar Questions
Consiedr the following x−t garaph to be parabolic. Draw the velocity-time graph and acceleration-time graph analyze the motion of the particle regarding its velocity and acceleration.
 .
.
View SolutionA : The area under acceleration - time graph is equal to velocity of object.
R : For an object moving with constant acceleration, position - time graph is a straight line.
View SolutionDraw the acceleration-time graphs for the given velocity-time graphs of a particle moving along x-axis.

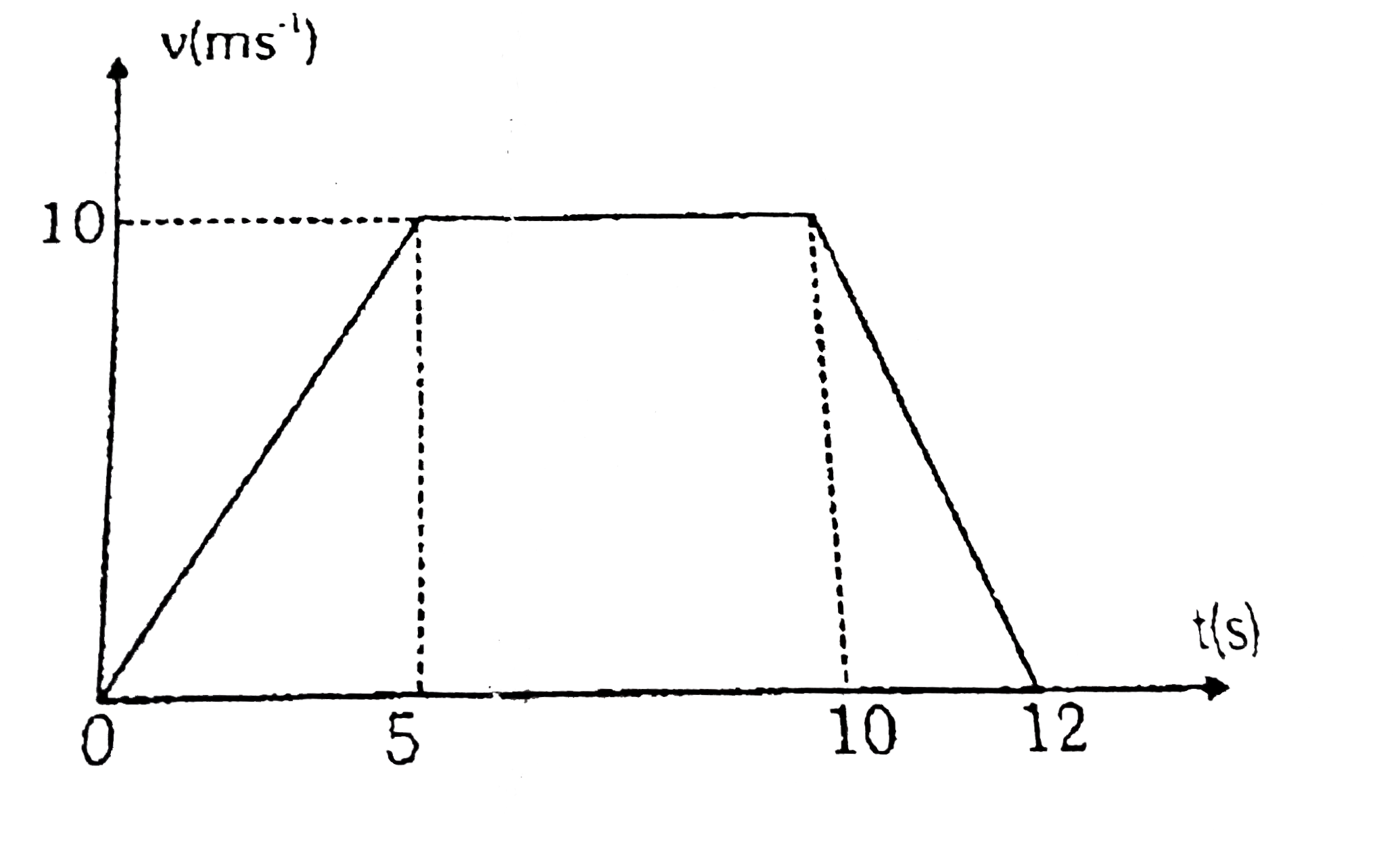
View SolutionDraw displacement time and acceleration -time graph for the given velocity-time graph
View SolutionAssertion At highest point of a projectile, dot product of velocity and acceleration is zero.
Reason At highest point, velocity and acceleration are mutually perpendicular.
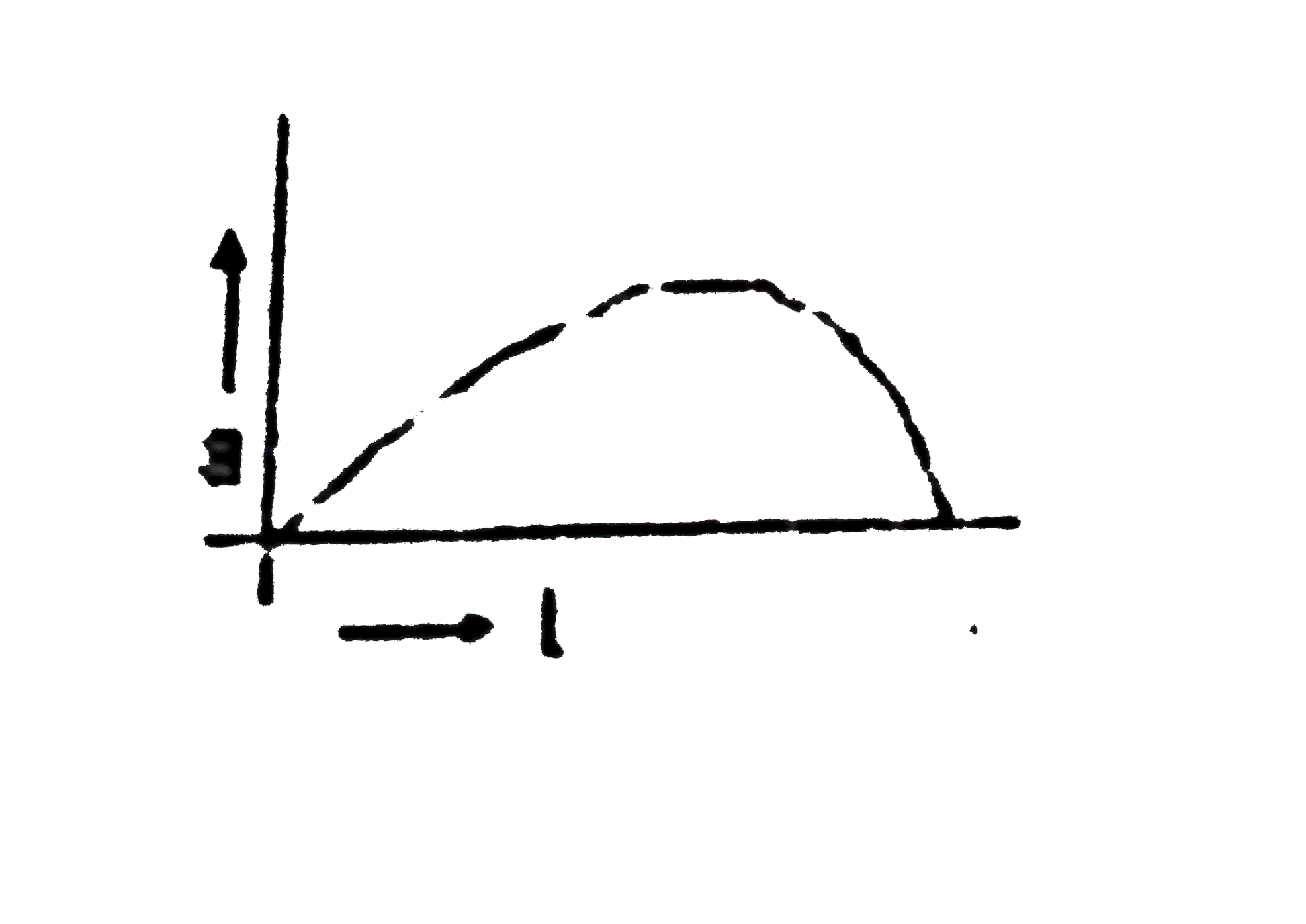
View SolutionA particle is moving in a straight line whose acceleration versus time graph is given. Assume that initial velocity is in the direction of acceleration. Then
which of the statement is correct between time t=0 to t=t0.
 .
.
View SolutionAssertion : In the x-t graph of a particle in SHM acceleration of particle at time t0 is positive but velocity is negative
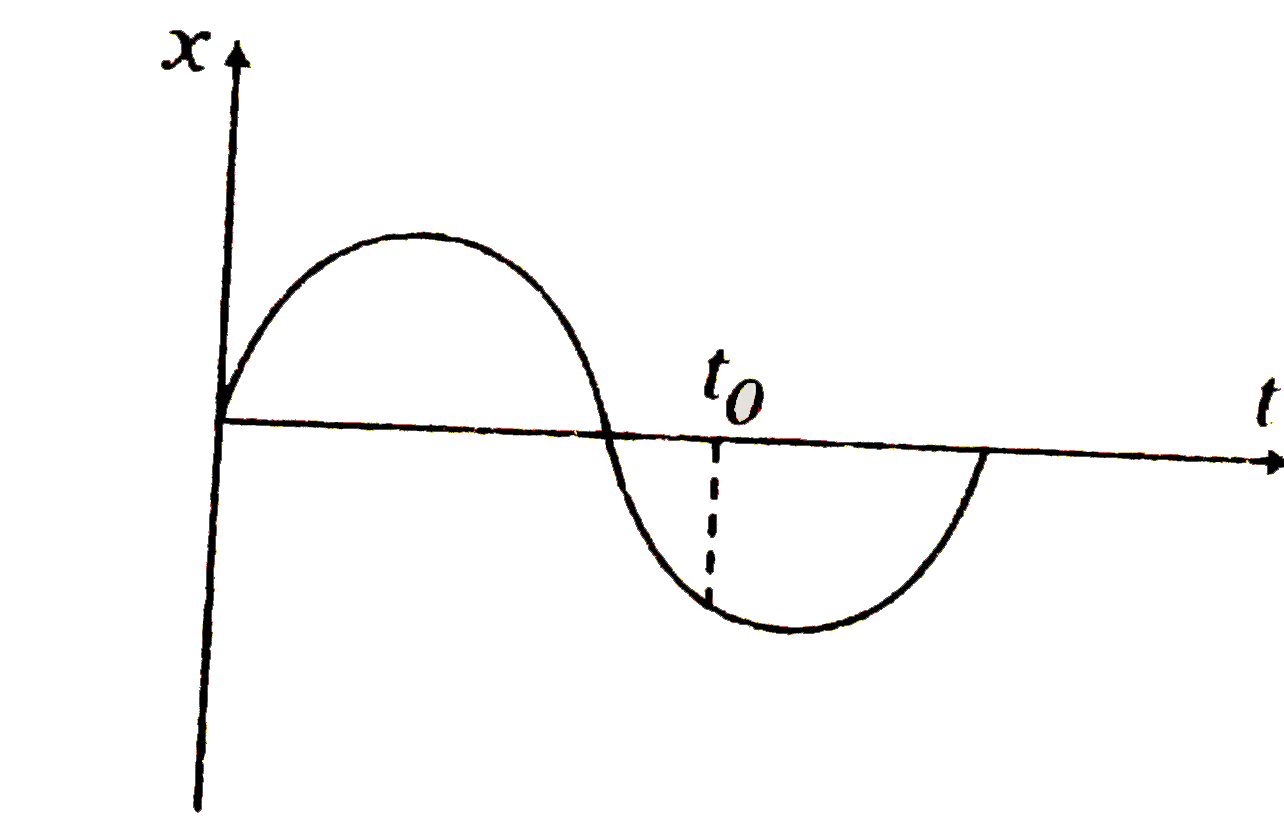
Reason :a∝−x and velocity is slope of x-t graph.
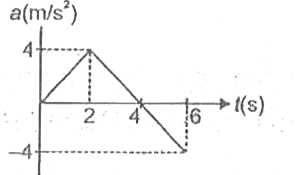
View SolutionFor the acceleration - time (a - t) graph shown in figure, the change in velocity of particle from t = 0 to t = 6 s is
View SolutionAssertion : We know the relation a=v.dvds . Therefore, if velocity of a particle is zero, then acceleration is also zero.
Reason : In the above equation, a is the instantaneous acceleration.
View SolutionObtain the formulae for displacement, velocity, acceleration and time period of a particle executing simple harmonic motion. When is the velocity of particle maximum and when zero ? Acceleration ?
View Solution
