Question

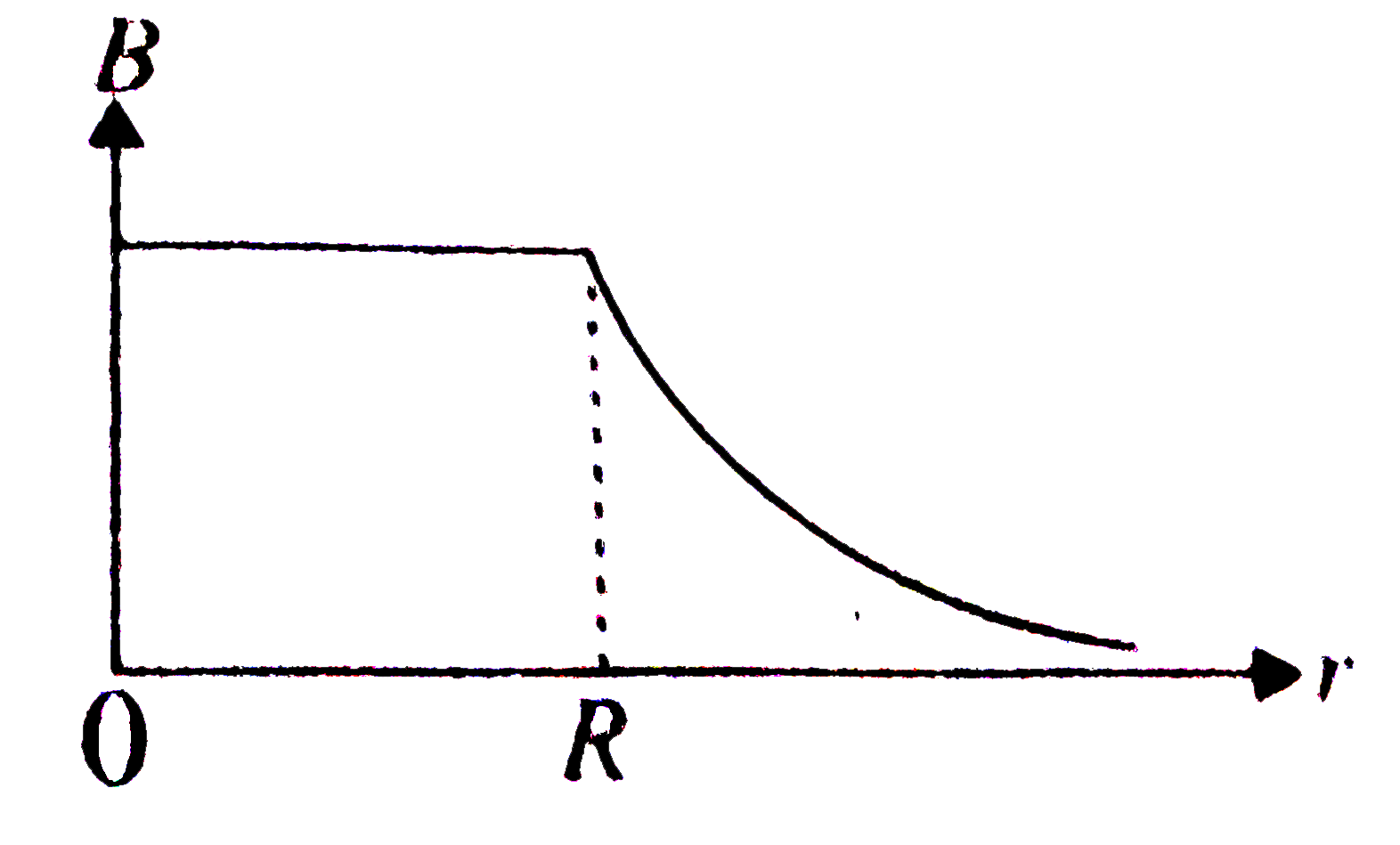
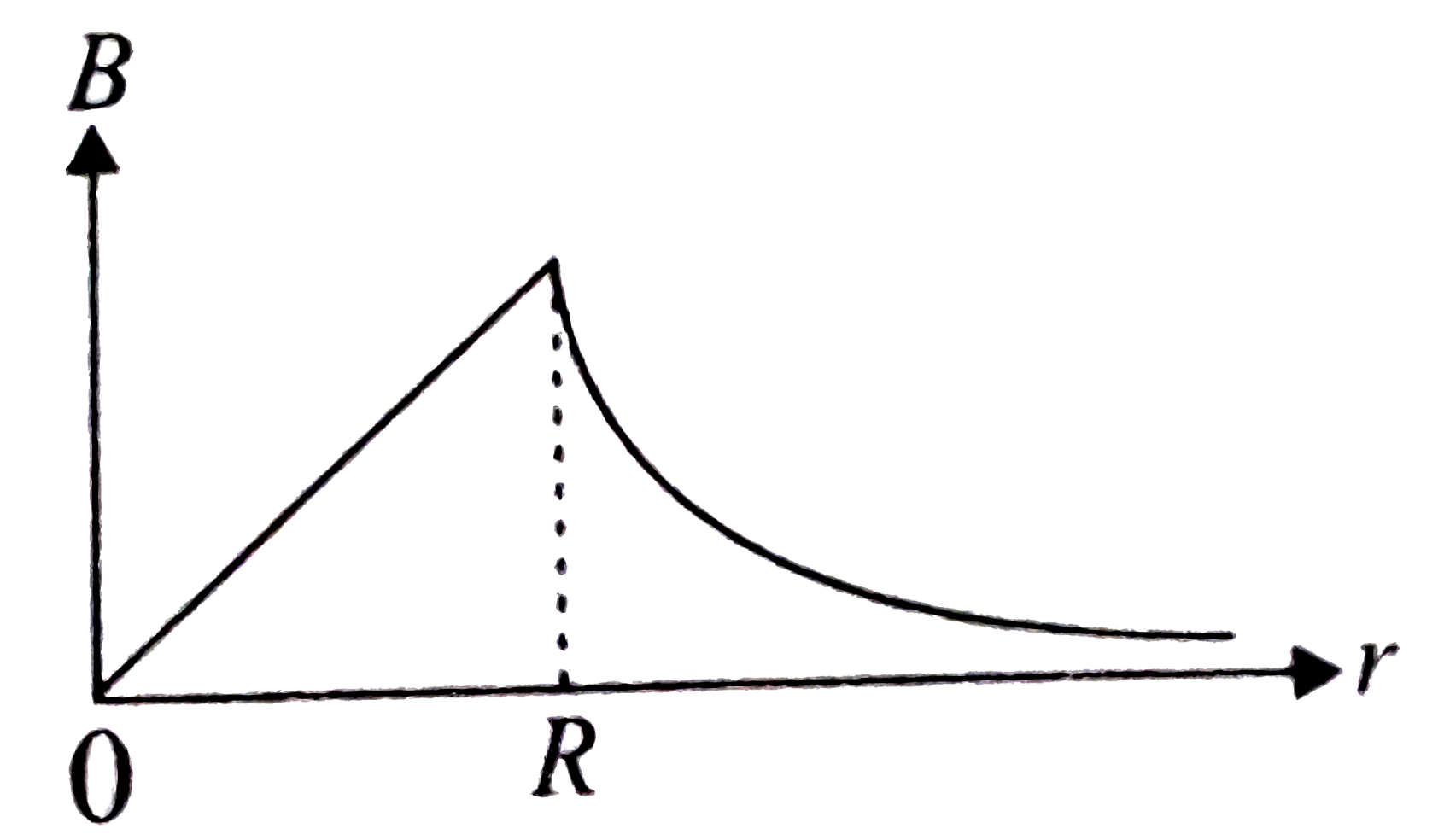
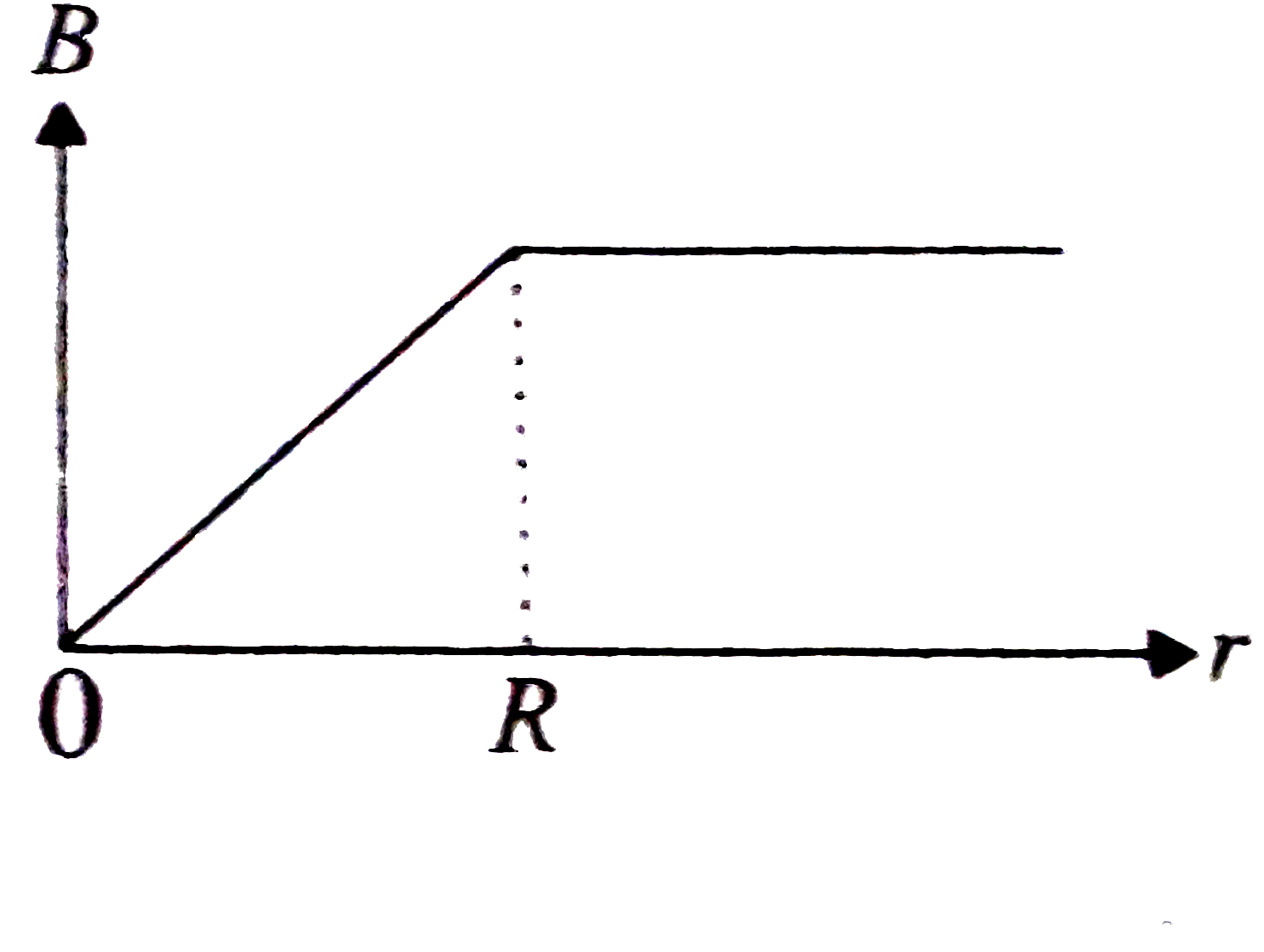
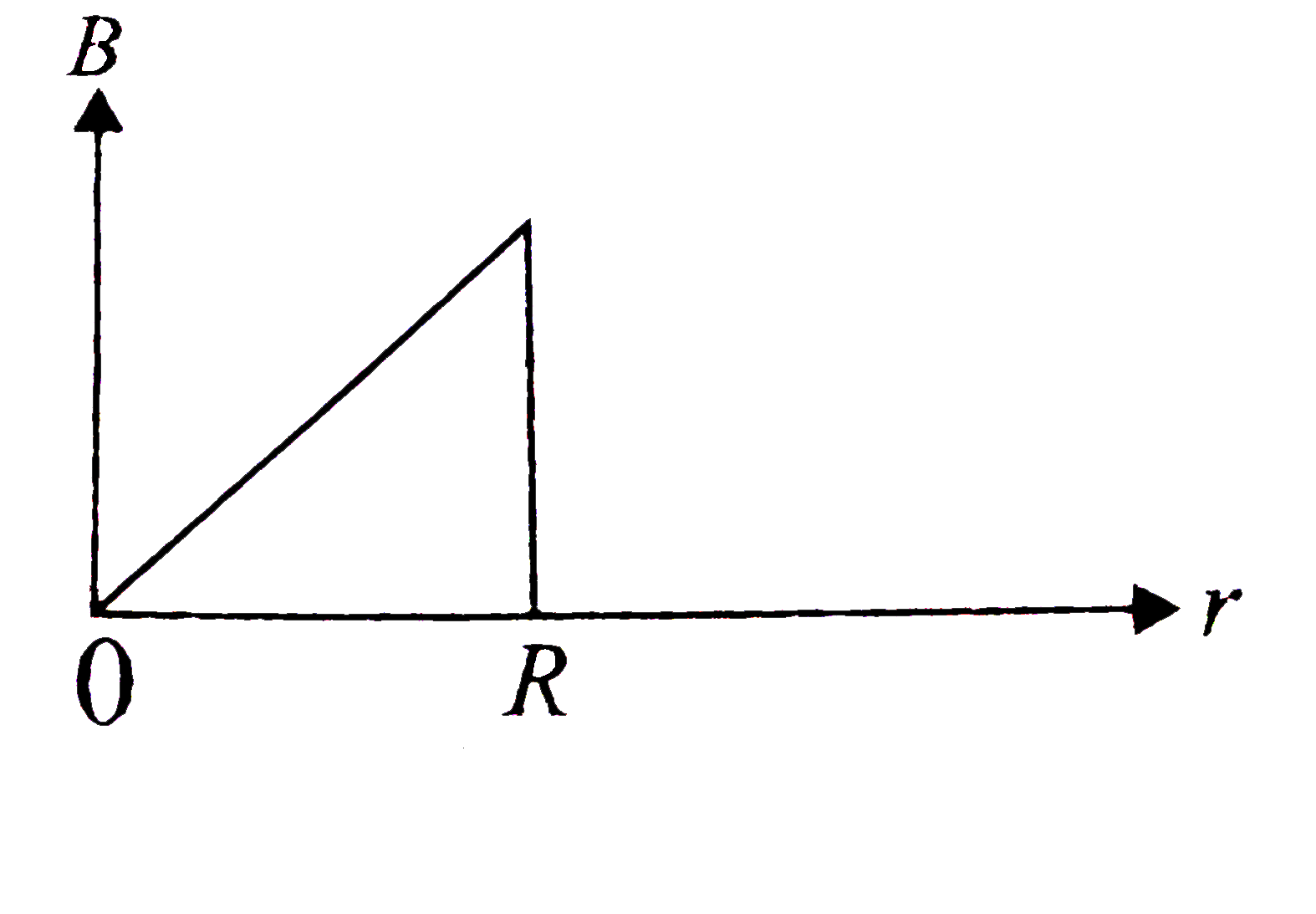
The correct plot of the magnitude of magnetic field $\overrightarrow{B}$ vs distance r from centre of the wire is, if the radius of wire is R

Options

A.
B.
C.
D.

Answer

B

Explanation

To solve the problem of determining the correct plot of the magnitude of the magnetic field $$\overrightarrow{B}$$ versus distance $$r$$ from the center of a wire with radius $$R$$, we can follow these steps:

Step 1: Understand the Magnetic Field Inside and Outside the Wire
1. Inside the Wire (\( r < R \)): The magnetic field \( B \) inside a long straight wire carrying a current \( I \) is given by the formula:
\( B = \frac{\mu_0 I}{2\pi R^2} r \)
where \( \mu_0 \) is the permeability of free space and \( r \) is the distance from the center of the wire. This indicates that the magnetic field \( B \) is directly proportional to \( r \) when \( r < R \).

2. Outside the Wire (\( r > R \)): The magnetic field outside the wire is given by:
\( B = \frac{\mu_0 I}{2\pi r} \)
This shows that the magnetic field \( B \) is inversely proportional to \( r \) when \( r > R \).

Step 2: Analyze the Behavior of \( B \) with Respect to \( r \)
- For \( r < R \): As \( r \) increases from 0 to \( R \), \( B \) increases linearly.
- For \( r > R \): As \( r \) continues to increase beyond \( R \), \( B \) decreases inversely.

Step 3: Sketch the Graph
- From \( r = 0 \) to \( r = R \): The graph will show a straight line with a positive slope (linear increase).
- From \( r = R \) onwards: The graph will show a curve that decreases, approaching the horizontal axis as \( r \) increases (inverse relationship).

Conclusion
The correct plot of the magnitude of the magnetic field \( B \) versus distance \( r \) from the center of the wire will show:
- A linear increase from the center of the wire to its surface (from \( r = 0 \) to \( r = R \)).
- A decrease in the magnetic field as the distance increases beyond the radius of the wire (from \( r = R \) onwards).

Final Answer
The correct plot is one that shows a linear increase up to \( r = R \) and then a decrease for \( r > R \).

---