An element A decays into element C by a two-step process :
A→B+.2He4
B→C+2e¯
Then.
A and C are isotopes
A and C are isobars
B and C are isotopes
A and B are isobars
The correct Answer is:a
To solve the problem, we need to analyze the decay process of element A into element C through an intermediate element B. The decay process is given as follows:
1. Decay of A to B:
A→B+α (where α is 42He)
Here, element A decays into element B and emits an alpha particle (which has a mass number of 4 and atomic number of 2).
2. Decay of B to C:
B→C+2β−
In this step, element B decays into element C and emits two beta particles (electrons).
Step 1: Determine the Mass and Atomic Numbers
- Let the mass number of element A be A and its atomic number be Z.
- After the first decay:
- Mass number of B: A−4
- Atomic number of B: Z−2
Step 2: Analyze the Decay of B
- For the second decay:
- Mass number of C: Since B decays to C and emits 2 beta particles (which do not change the mass number), the mass number of C remains the same as B.
- Therefore, mass number of C: A−4
- Atomic number of C: Since B has an atomic number of Z−2 and emits 2 beta particles (which increase the atomic number by 2), the atomic number of C will be:
Z−2+2=Z
Step 3: Summarize the Relationships
- We have:
- Mass number of B: A−4, Atomic number of B: Z−2
- Mass number of C: A−4, Atomic number of C: Z
Step 4: Identify Relationships Between Elements
- Since the atomic number of C is Z and that of A is also Z, elements A and C have the same atomic number, making them isotopes.
- Since B has a different atomic number than A and C, it cannot be an isotope of either.
- B and C have the same mass number (A−4), making them isobars.
Conclusion
- A and C are isotopes (same atomic number, different mass numbers).
- B and C are isobars (same mass number, different atomic numbers).
- A and B are neither isotopes nor isobars.
Final Answer
The correct option is that A and C are isotopes.
A→B+α (where α is 42He)
Here, element A decays into element B and emits an alpha particle (which has a mass number of 4 and atomic number of 2).
B→C+2β−
In this step, element B decays into element C and emits two beta particles (electrons).
- Let the mass number of element A be A and its atomic number be Z.
- After the first decay:
- Mass number of B: A−4
- Atomic number of B: Z−2
- For the second decay:
- Mass number of C: Since B decays to C and emits 2 beta particles (which do not change the mass number), the mass number of C remains the same as B.
- Therefore, mass number of C: A−4
- Atomic number of C: Since B has an atomic number of Z−2 and emits 2 beta particles (which increase the atomic number by 2), the atomic number of C will be:
Z−2+2=Z
- We have:
- Mass number of B: A−4, Atomic number of B: Z−2
- Mass number of C: A−4, Atomic number of C: Z
- Since the atomic number of C is Z and that of A is also Z, elements A and C have the same atomic number, making them isotopes.
- Since B has a different atomic number than A and C, it cannot be an isotope of either.
- B and C have the same mass number (A−4), making them isobars.
- A and C are isotopes (same atomic number, different mass numbers).
- B and C are isobars (same mass number, different atomic numbers).
- A and B are neither isotopes nor isobars.
The correct option is that A and C are isotopes.
Topper's Solved these Questions
- NUCLEIBOOK - NCERT FINGERTPS ENGLISHCHAPTER - NUCLEIEXERCISE - HOTS
7 Videos
- NUCLEIBOOK - NCERT FINGERTPS ENGLISHCHAPTER - NUCLEIEXERCISE - EXEMPLAR PROBLEMS
7 Videos
- MOVING CHARGES AND MAGNETISM BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOVING CHARGES AND MAGNETISM EXERCISE - Assertion And Reason
15 Videos
- PRACTICE PAPPERBOOK - NCERT FINGERTPS ENGLISHCHAPTER - PRACTICE PAPPEREXERCISE - Practice Paper 3
50 Videos
Similar Questions

Process A→B represents
View SolutionXe+O2F2→A+B
A+H2O→B+C+Xe
A, B and C are:
View SolutionXeF2+HCl→A+B+C
View Solution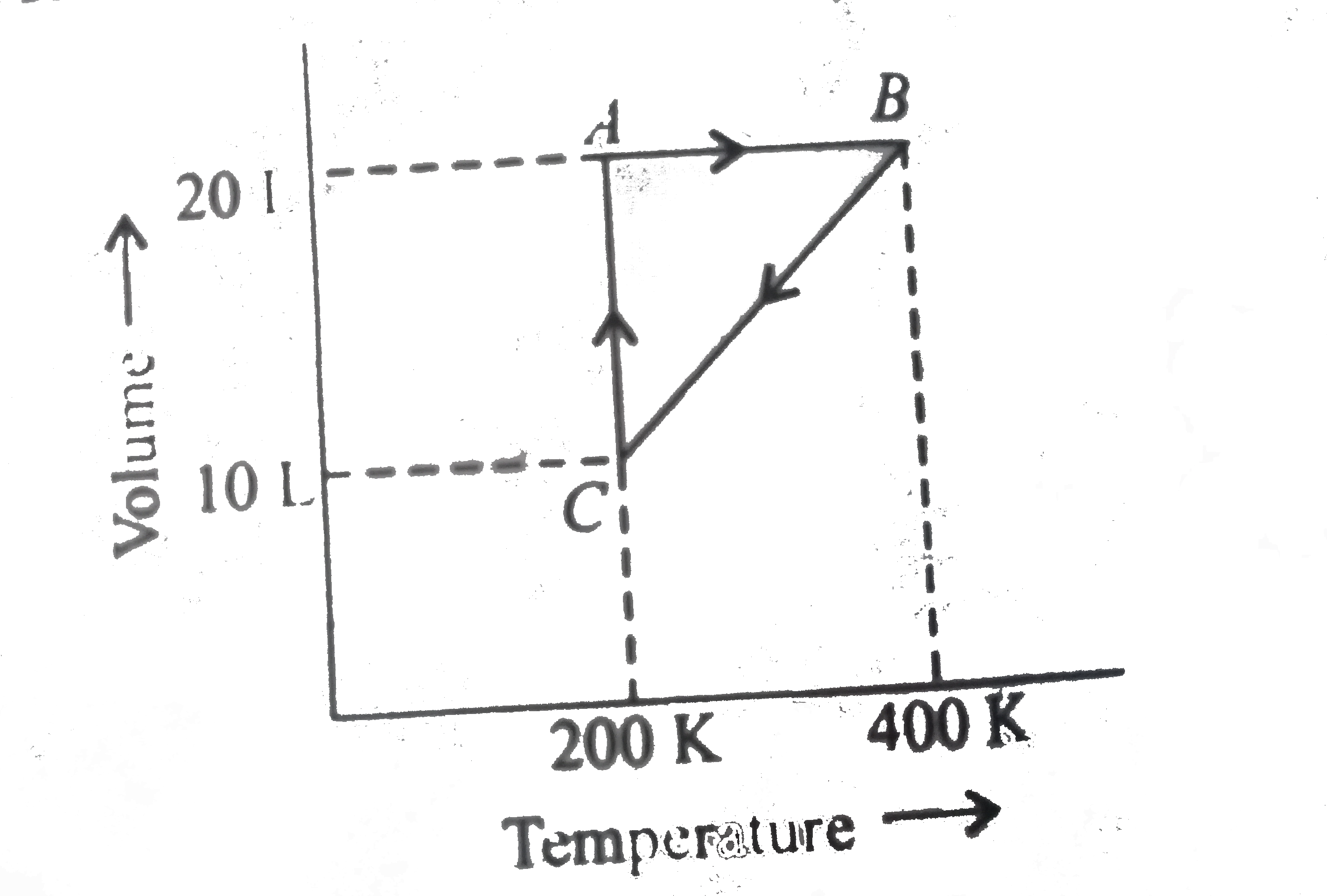
The process which occurs in going from B→C is
View SolutionIn a certain hypothetical radioactive decay process, species A decays into spesies B and species B decays intoC according to the reactions
A→2B+particles +energyB→2C+particles +energy
The decay constant for species B is λ2=100s−1. Initially, 104 moles of species of A were present while there was no none of B and C. It was found that species B reaches its maximum number at a time t0=21n(10)s. Calcualte the value of maximum number of moles of B.
View SolutionA reaction is found to proceed in two steps as A+B→E (slow),, A+E→C+D (fast). Write the law expresison and overall balanced equation.
View SolutionAn ideal gas (2.0 moles) is carried round a cycle as shown. If the process b→c is isothermal and CV=3cal/mol/K. Determine
a. work done,
b. change in internal energy,
c. heat supplied to the system during processes a→b, b→c and c→a.
View SolutionA fixed mass of gas is taken through a process A→B→C→A. Here A→B is isobaric, B→C is adiabatic and C→Ais isothermal. Find pressure at C
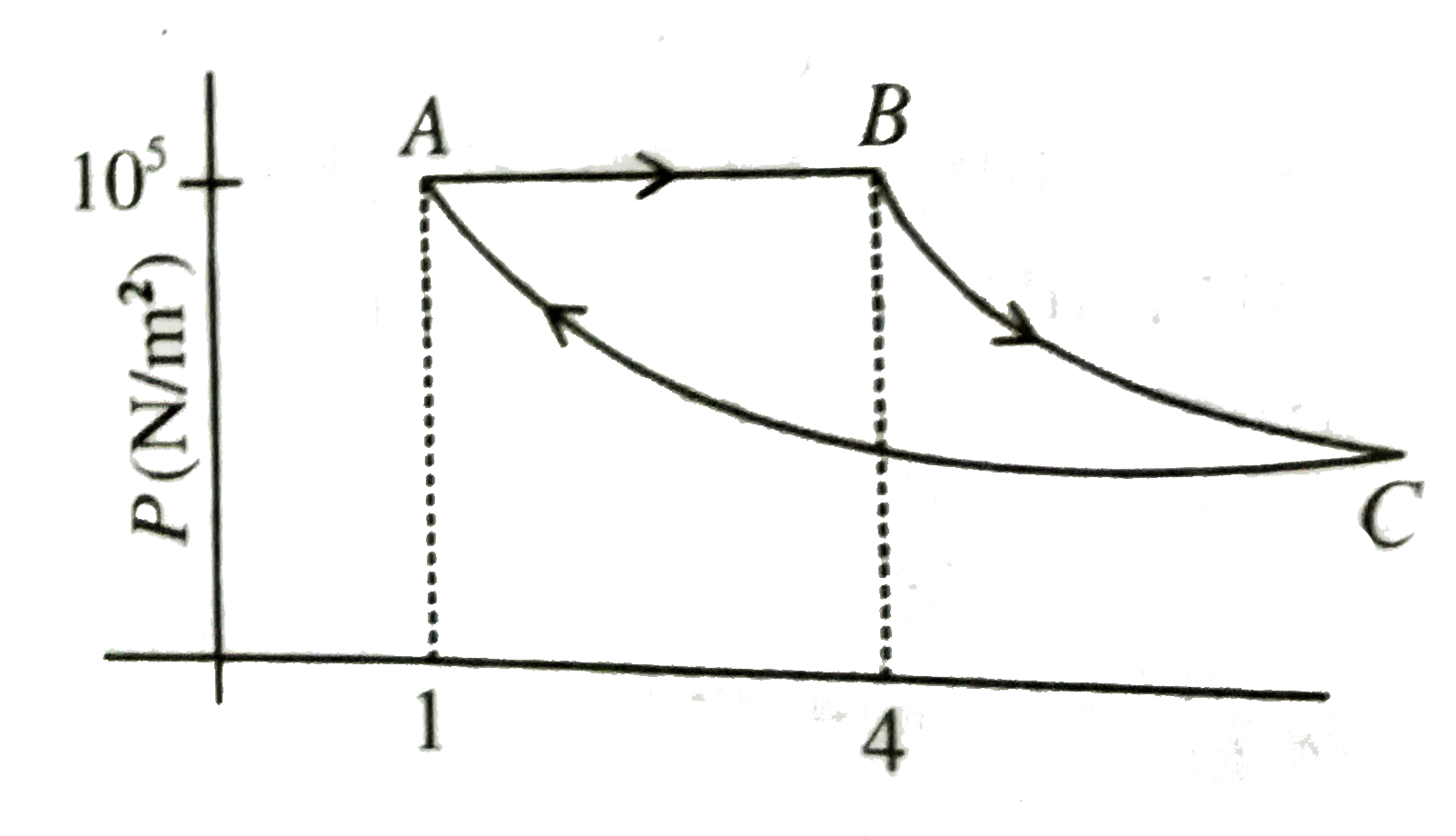
.
View SolutionA fixed mass of gas is taken through a process A→B→C→A. Here A→B is isobaric, B→C is adiabatic and C→Ais isothermal. Find volume at C.
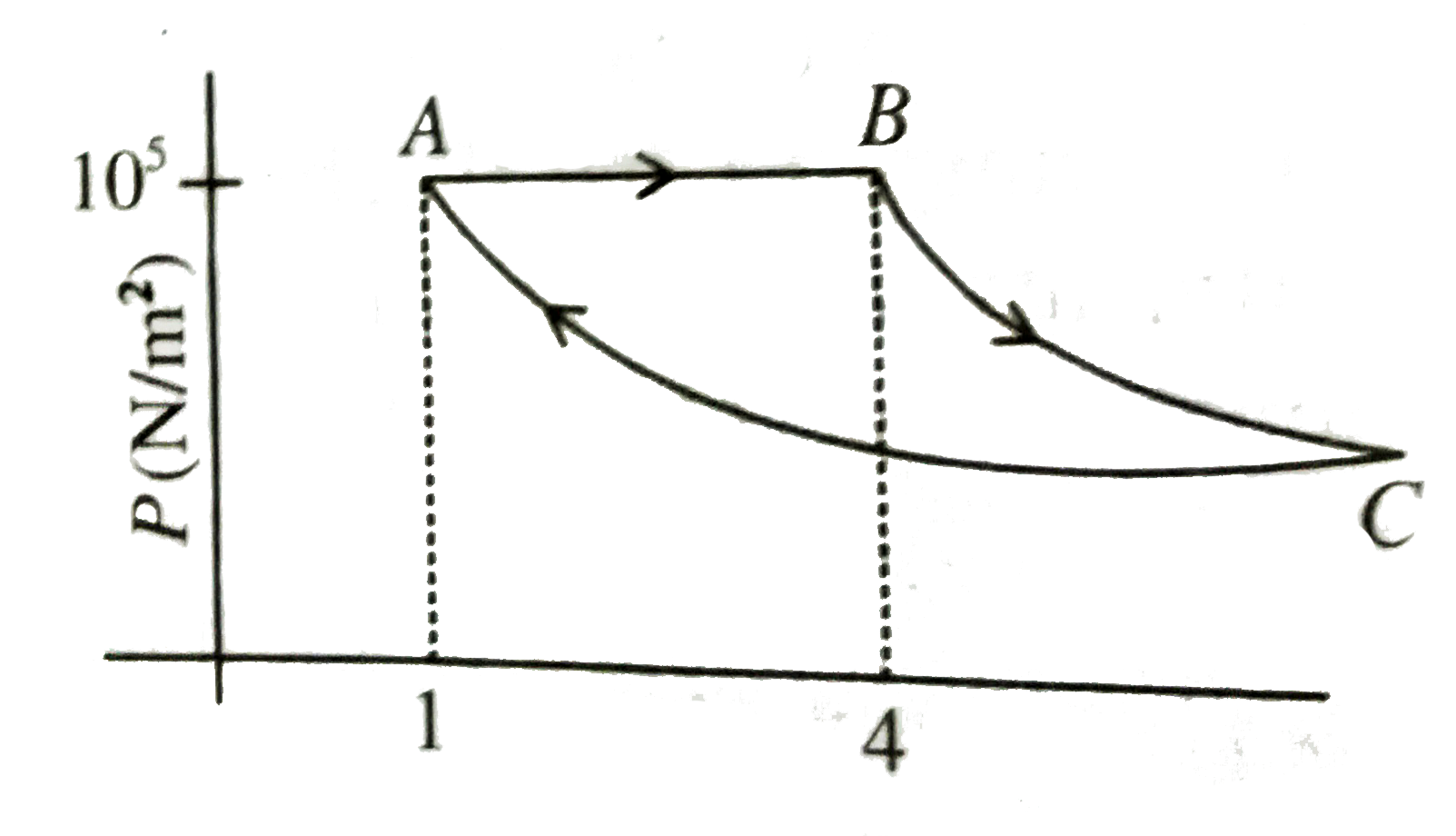
View SolutionA fixed mass of gas is taken through a process A→B→C→A. Here A→B is isobaric, B→C is adiabatic and C→Ais isothermal. Find work done is the process ( take γ=1.5).
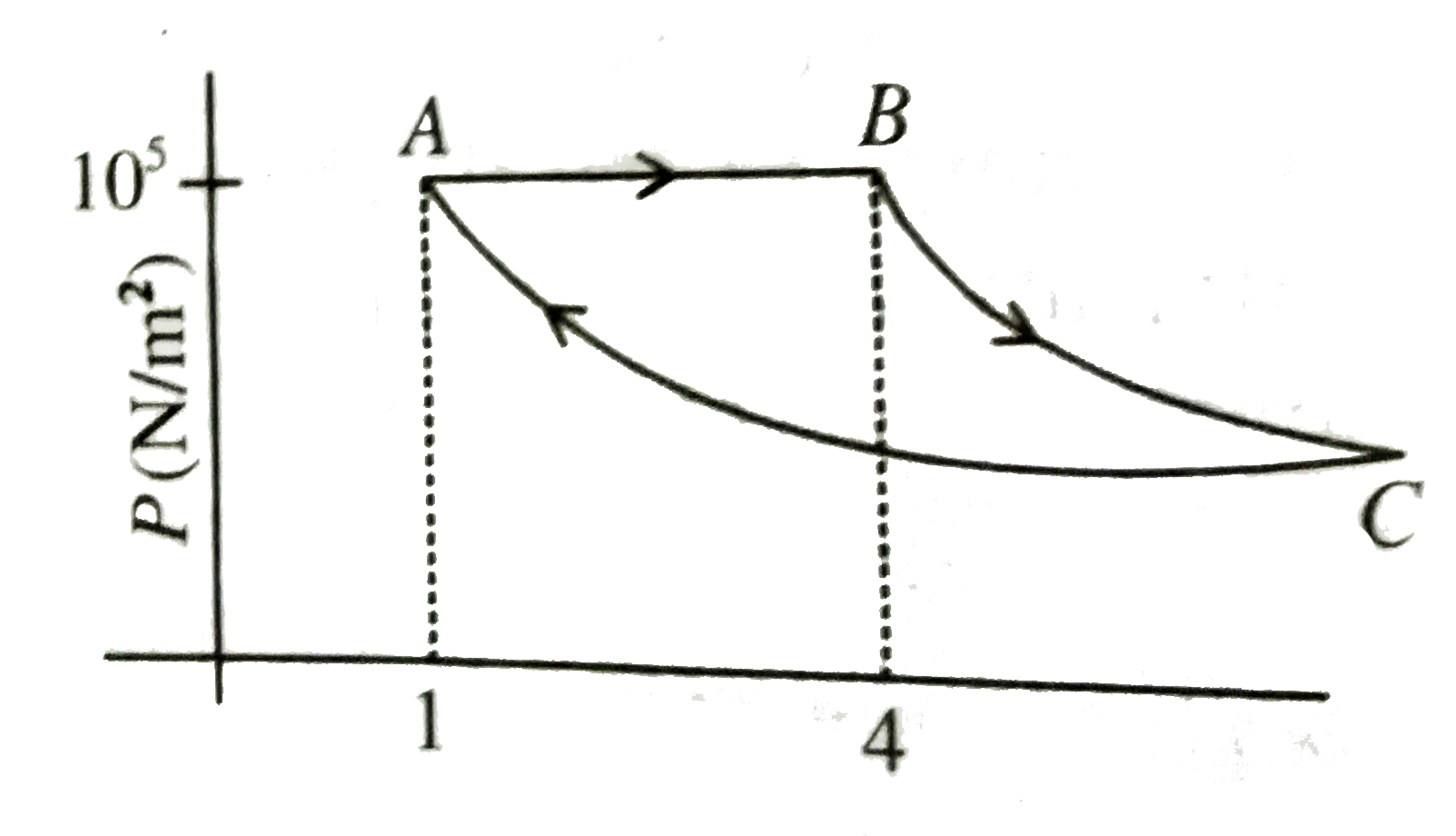
View Solution
