A particle executing SHM. The phase difference between acceleration and displacement is
0
π2
π
2π
The correct Answer is:C
To find the phase difference between acceleration and displacement for a particle executing Simple Harmonic Motion (SHM), we can follow these steps:
1. Understand the equations of SHM:
The displacement x of a particle in SHM can be expressed as:
x(t)=Acos(ωt)
where A is the amplitude and ω is the angular frequency.
2. Determine the velocity:
The velocity v is the time derivative of displacement:
v(t)=dxdt=−Aωsin(ωt)
3. Determine the acceleration:
The acceleration a is the time derivative of velocity:
a(t)=dvdt=−Aω2cos(ωt)
4. Identify the forms of displacement and acceleration:
From the equations derived:
- Displacement: x(t)=Acos(ωt)
- Acceleration: a(t)=−Aω2cos(ωt)
5. Analyze the phase of displacement and acceleration:
The displacement x(t) is represented by cos(ωt), while the acceleration a(t) can be rewritten as:
a(t)=−Aω2cos(ωt)=Aω2cos(ωt+π)
This indicates that the acceleration is π radians (or 180 degrees) out of phase with the displacement.
6. Conclusion:
Therefore, the phase difference between acceleration and displacement is:
Phase difference=π radians
Final Answer:
The phase difference between acceleration and displacement in SHM is π radians.
---
The displacement x of a particle in SHM can be expressed as:
x(t)=Acos(ωt)
where A is the amplitude and ω is the angular frequency.
The velocity v is the time derivative of displacement:
v(t)=dxdt=−Aωsin(ωt)
The acceleration a is the time derivative of velocity:
a(t)=dvdt=−Aω2cos(ωt)
From the equations derived:
- Displacement: x(t)=Acos(ωt)
- Acceleration: a(t)=−Aω2cos(ωt)
The displacement x(t) is represented by cos(ωt), while the acceleration a(t) can be rewritten as:
a(t)=−Aω2cos(ωt)=Aω2cos(ωt+π)
This indicates that the acceleration is π radians (or 180 degrees) out of phase with the displacement.
Therefore, the phase difference between acceleration and displacement is:
Phase difference=π radians
The phase difference between acceleration and displacement in SHM is π radians.
Topper's Solved these Questions
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - OSCILLATIONS EXERCISE - Higher Order Thinking Skills8videos
OSCILLATIONS
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - OSCILLATIONS EXERCISE - Exemplar Problems9videos
OSCILLATIONS
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - NCERT Exemplar6videos
MOTION IN A STRAIGHT LINE
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - PHYSICAL WORLDEXERCISE - Assertion And Reason10videos
PHYSICAL WORLD
Similar Questions
Knowledge Check
- Question 1 - Select One
A particle executing SHM. The phase difference between velocity and displacement is
A0Bπ2CπD2π - Question 2 - Select One
Two particles execute SHMs of the same amplitude and frequency along the same straight line. They cross one another when going in opposite direction. What is the phase difference between them when their displacements are half of their amplitudes ?
A60∘B30∘C120∘D150∘
The KE and PE , at is a particle executing SHM with amplitude A will be equal when its displacement is
View SolutionThe KE and PE , at is a particle executing SHM with amplitude A will be equal when its displacement is
View SolutionEnergy of particle executing SHM depends upon
View SolutionThe phase difference between two particies executing shm is π/2. What does it mean?
View SolutionThe velocity time graph of a particle executing SHM is shown. The maximum acceleration of the particle is nπm/s2, where n is______.
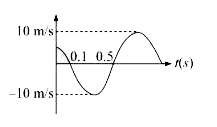 View Solution
View SolutionA particle is executing SHM along a straight line. Then choose the correct statement
View Solution

