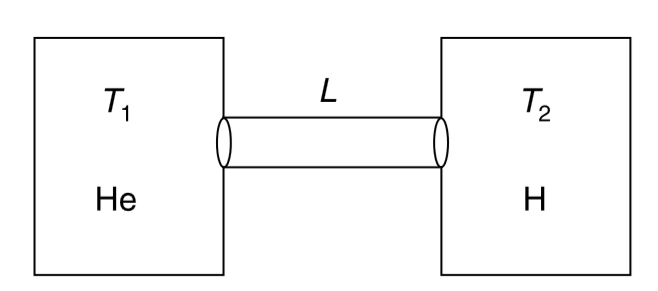
Two identical adiabatic vessels A and B each contain n mole of a monoatomic and diatomic gas respectively. Both the vessels are connected by a rod of length 1 and cross-sectional area A. Thermal conductivity of rod material is k and lateral surface of the rod is insulated. At any time capacity of the rod and the vessels, find the time when the temperature difference of the vessels becomes half the initial temperature difference.
t=15nRl16kAIn(2)
Topper's Solved these Questions
- THERMODYNAMICSBOOK - AAKASH SERIESCHAPTER - THERMODYNAMICSEXERCISE - QUESTIONS FOR DESCRIPTIVE ANSWERS
7 Videos
- THERMODYNAMICSBOOK - AAKASH SERIESCHAPTER - THERMODYNAMICSEXERCISE - Problem
60 Videos
- THERMODYNAMICSBOOK - AAKASH SERIESCHAPTER - THERMODYNAMICSEXERCISE - NUMERICAL EXERCISE (LEVEL-1)
19 Videos
- THERMAL PROPERTIES OF MATTERBOOK - AAKASH SERIESCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL - II) PRACTICE SHEET (ADVANCED) Integer/Subjective Type Questions
2 Videos
- THERMOMETRY BOOK - AAKASH SERIESCHAPTER - THERMOMETRY EXERCISE - Numerical Exercise (LEVEL- 1)
11 Videos
Similar Questions
Two identical adiabatic containers of negligible heat capacity are connected by conducting rod of length L and cross sectional area A. Thermal conductivity of the rod is k and its curved cylindrical surface is well insulated from the surrounding. Heat capacity of the rod is also negligible. One container is filled with n moles of helium at temperature T1 and the other one is filled with equal number of moles of hydrogen at temperature T2(<T1). Calculate the time after which the temperature difference between two gases will becomes half the initial difference.
View Solution" A metal rod of area of cross section A has length L and coefficient of thermal conductivity K The thermal resistance of the rod is "
View Solution
Knowledge Check
Two adiabatic vessels, each containing the same mass m of water but at different temperatures, are connected by a rod of length L, cross-section A, and thermal conductivity K. the ends of the rod are inserted into the vessels, while the rest of the rod is insulated so that .there is negligible loss of heat into the atmosphere. The specific heat capacity of water is s, while that of the rod is negligible. The temperature difference between the two vessels reduces to l/e of its original value after a time, δt. The thermal conductivity (K) of the rod may be expressed by:
AmsLAδtBemsLAδtCmsL2eAδtDmsL2AδtA metal rod of area of cross section A has length L and coefficient of thermal conductivity K the thermal resistance of the rod is .
ALKABKLLCKALDAKLThe ratio of thermal conductivity of two rods of different material is 5:4. The two rods of same area of cross-section and same thermal resistance will have the lengths in the ratio
A4:5B9:1C1:9D5:4
Two bodies each of mass m, having specific heats s, are connected by ametal rod of negligible heat capacity of length l, area of cross section A and thermal conductivity k. Initially both bodies are at different temperatures, find the time taken for the temperature difference between the two bodies to become half of the. initial value.
View SolutionFigure shown two adiabatic vessels, each containing a mass m of water at different temperature. The ends of a metal rod of length L, area of cross section. A and thermal conductivity K, are inserted in the water as shown in the figure. Find the time taken for the difference between the temperature in the vessels to become half of the original value. The specific heat capacity of water is s. Neglect the heat capacity of the rod and the container and any loss of heat top the atmosphere.

View SolutionFigure shown two adiabatic vessels, each containing a mass m of water at different temperature. The ends of a metal rod of length L, area of cross section A and thermal conductivity K, are inserted in the water as shown in the figure. Find the time taken for the difference between the temperature in the vessels to become half of the original value. The specific heat capacity of water is s. Neglect the heat capacity of the rod and the container and any loss of heat to the atmosphere.

View SolutionThe ratio of the thermal conductivities of two different materials is 1:2. The thermal resistance of the rods of these materials having the same thickness are equal. Find the ratio of the length of rods.
View SolutionThe ratio of thermal conductivity of two rods of different material is 5:4. The two rods of same area of cross-section and same thermal resistance will have the lengths in the ratio
View Solution
