The system shown is figure consists of 3 springs and two rods. If the temperature of the rod is increased by ΔT, then the total energy stored in three springs is β×99484kL2α2(ΔT)2. Determine the value of β. The spring are initially relaxed and there is no friction anywhere. For rod the coefficient of linear expansion is α
_E01_089_Q01.png)
Let x1, x2 and x3 be the compressions in the three springs, then
x1+x2+x3=LαΔT+L2αΔT=32LαΔT ………..(1)
Considering the F.B.D.s of the rod requires rods
Equilibrium of the rod requires that
x1=2x2==3x3........(2)
∴x1+x12+x33=32LαΔT
⇒x1=911LαΔT
∴ Energy stored in spring of spring constant k.
E1=12kx21=81242kL2α2ΔT2
Similarly
E2=81484kL2α2ΔT2 and E3=27242kL2α2ΔT2
Topper's Solved these Questions
Similar Questions
A composite rod is made by joining a copper rod, end to end, with a second rod of different material but of the same area of cross section. At 25∘C, the composite rod is 1m long and the copper rod is 30cm long. At 125∘C the length of the composite rod increases by 1.91mm. When the composite rod is prevented from expanding by holding it between two rigid walls, it is found that the constituent rods have remained unchanged in length inspite of rise of temperature. Find young's modulus and the coefficient of linear expansion of the second rod (Y of copper =1.3×1010N/m2 and a of copper =17×10−6/K).
View SolutionA composite rod is made by joining a copper rod, end to end, with a second rod of different material but of the same area of cross section. At 25∘C, the composite rod is 1m long and the copper rod is 30cm long. At 125∘C the length of the composte rod increases by 1.91mm. When the composite rod is prevented from expanding by bolding it between two rigid walls, it is found that the constituent reds have remained unchanged in length in splite of rise of temperature. Find yong's modulus and the coefficient of linear expansion of the second red (Y of copper =1.3×1010N/m2 and a of copper =17×10−6/K).
View SolutionConsider the plane of the paper to be vertical plane with direction of 'g' as shown in the figure. A rod (MM') of mass 'M' and carrying a current I. The rod is suspended vertically through two insulated spring of spring constant K at two ends. A uniform magnetic field is applied perpendicular to the plane of the paper such that the potential energy stored in the spring, in equilibrium position is zero. If the rod is slightly displaced in the vertically direction from the position of equilibrium, then the time period of oscillation is
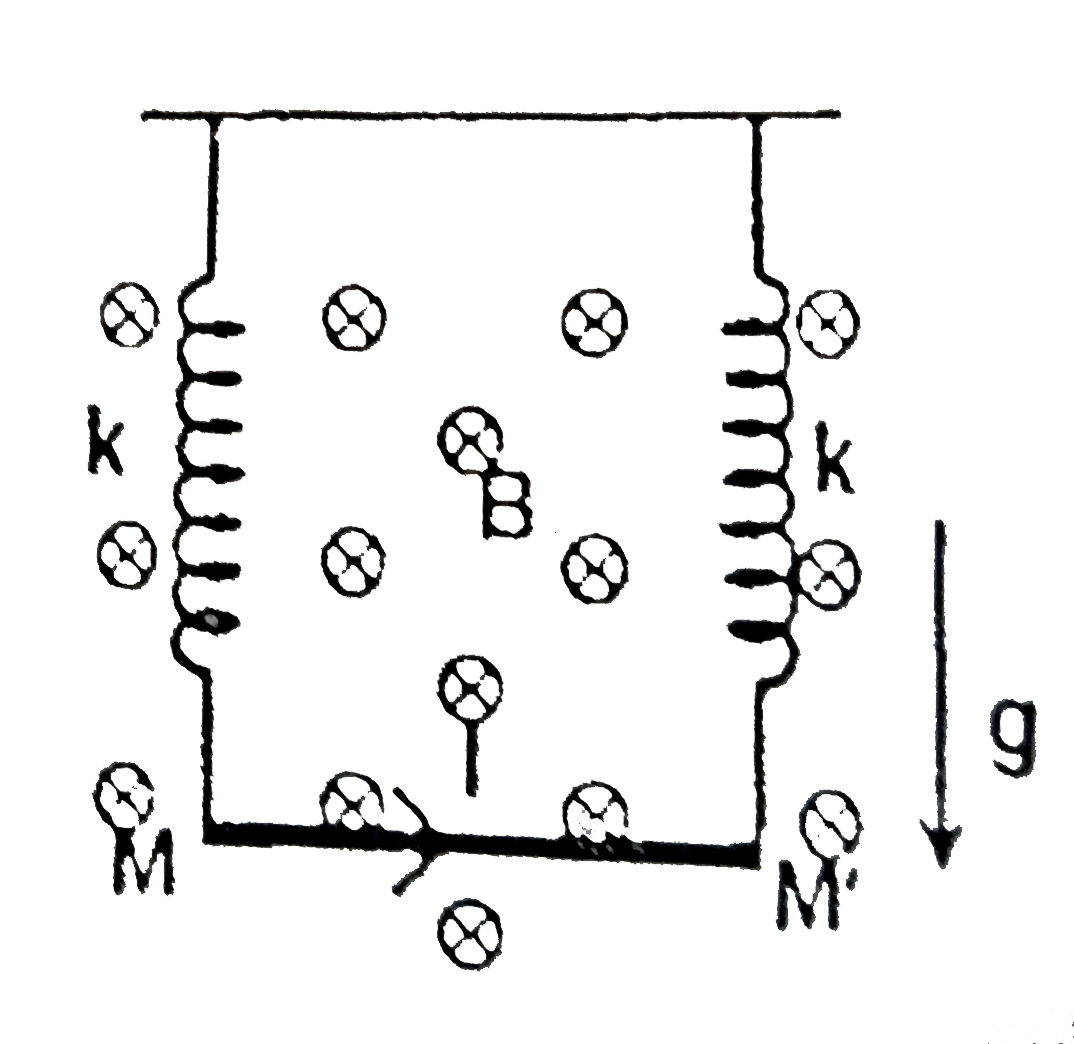View SolutionA meter scale calibarated for temperature T is used to measure the length of a steel rod. Length of steel rod measured by metal scale at temperature 2T is L. Length of the rod measured by metal scale at temperature T is [αs:Coefficient of linear expansion of metal scale, αR : Coefficient of linear expansion of steel rod]
View Solution
The rectangular plate shown if Fig. 1.7 has an area Ai. If the temperature increases by ΔT, each dimension increases according to ΔL=αLΔT, where α is the average coefficient of linear expansion. Show that the increase in area is ΔA=2αAiΔT. What approzimation does this expansion assume?View SolutionIn a vernier callipers the main scale and the vernier scale are made up different materials. When the room temperature increases by ΔT∘C, it is found the reading of the instrument remains the same. Earlier it was observed that the front edge of the wooden rod placed for measurement crossed the Nth main scale division and N + 2 MSD coincided with the 2nd VSD. Initially, 10 VSD coincided with 9MSD. If coefficient of linear expansion of the main scale is α1 and that of the vernier scale is α2 then what is the value of α1/α2 ? (Ignore the expansion of the rod on heating)
View SolutionTwo rods of equal cross sections, one of copper and the other of steel, are joined to form a composite rod of length 2.0 m at 20∘C, the length of the copper rod is 0.5 m. When the temperature is raised to 120∘C, the length of composite rod increases to 2.002m. If the composite rod is fixed between two rigid walls and thus not allowed to expand, it is found that the lengths of the component rods also do not change with increase in temperature. Calculate Young's moulus of steel. (The coefficient of linear expansion of copper, αc=1.6×10−5∘C and Young's modulus of copper is 1.3×1013N/m2).
View SolutionAccording to the principle of conservation of linear momentum, if the external force acting on the system is zero, the linear momentum of the system will remain conserved. It means if the centre of mass of a system is initially at rest, it will remain, at rest in the absence of external force, that is, the displacement of centre of mass will be zero.
Two blocks of masses 'm'and '2m' are placed as shown in Fig. There is no friction anywhere. A spring of force constant k is attached to the bigger block. Mass 'm' is kept in touch with the spring but not attached to it. 'A' and 'B' are two supports attached to '2m'. Now m is moved towards left so that spring is compressed by distance 'x' and then the system is released from rest.
Find the relative velocity of the blocks after 'm' leaves contact with the spring.View SolutionIf two rods of length L and 2L having coefficients of linear expansion α and 2α respectively are connected so that total length becomes 3L, the average coefficient of linear expansion of the composite rod equals
View SolutionIf two rods of length L and 2L having coefficients of linear expansion α and 2α respectively are connected so that total length becomes 3L, the average coefficient of linear expansion of the composite rod equals
View Solution