Find the magnitude of the magnetic induction B of a magnetic field generated by a system of thin conductors, alon which a curren i is flowing at the point A (0,R,0) which is the centre of the circular conductor of radius R. The ring is yz plane.
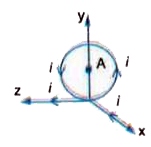
B=μ0i4πR√2(2π2−2π+1)
Topper's Solved these Questions
- ELECTROMAGNETICSBOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETICSEXERCISE - ADDITIONAL EXERCISE
6 Videos
- ELECTROMAGNETICSBOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETICSEXERCISE - PROBLEMS (LEVEL -I)
30 Videos
- ELECTROMAGNETIC WAVESBOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - EXERCISE -II
20 Videos
- ELECTROSTATICSBOOK - AAKASH SERIESCHAPTER - ELECTROSTATICSEXERCISE - ADDITIONAL PRACTICE EXERCISE (PRACTICE SHEET (ADVANCED) INTEGER TYPE QUESTIONS)
4 Videos
Similar Questions
Find the magnitude of the magnetic induction B of a magnetic field generated by a system of thin conductors along which a current I is flowing at a point A (O, R, O), that is the centre of a circular conductor of radius R. The ring is in yz plane.

View SolutionFind the magnitude of the magnetic induction B of a magnetic field generated by a system of thin conductors along which a current I is flowing at a point A (O, R, O), that is the centre of a circular conductor of radius R. The ring is in yz plane.

View Solution
Knowledge Check
Find the magnitude of the magnetic induction B of a magnetic field generated by a system of thin conductors along which a current I is flowing at a point A (O, R, O), that is the centre of a circular conductor of radius R. The ring is in yz plane.
 AB=μ0i4πR√(2π2−2π+1)BB=μ0i4πR√2(2π2−2π+1)CB=μ0i2πR√(2π2−2π+1)DNone of these
AB=μ0i4πR√(2π2−2π+1)BB=μ0i4πR√2(2π2−2π+1)CB=μ0i2πR√(2π2−2π+1)DNone of theseA cell is connected between two points of a uniformly thick circular conductor and i1andi2 are the currents flowing in two parts of the circular conductor of radius a The magnetic field at the centre of the loop will be
AzeroBμ04π(I1−I2)Cμ02a(I1+I2)Dμ0a(I1+I2)A long straight conductor carrying a current i is bent to form an almost complete circular loop of radius r on it. The magnetic field at the centre of the loop
 Ais directed into the paperBis directed out of the paperChas magnitude μ0i2r(1−1π)Dhas magnitude μ(0)i2r(1+1π)
Ais directed into the paperBis directed out of the paperChas magnitude μ0i2r(1−1π)Dhas magnitude μ(0)i2r(1+1π)
a. A conductor in the shape of a square of edge length l=0.4m carries a current i=10.0A. Calculate the magnitude and direction of magnetic field at the centre of the square.
b. If this conductor is formed into a single circular turn and carries the same current. what is the value of the magnetic field at the centre.
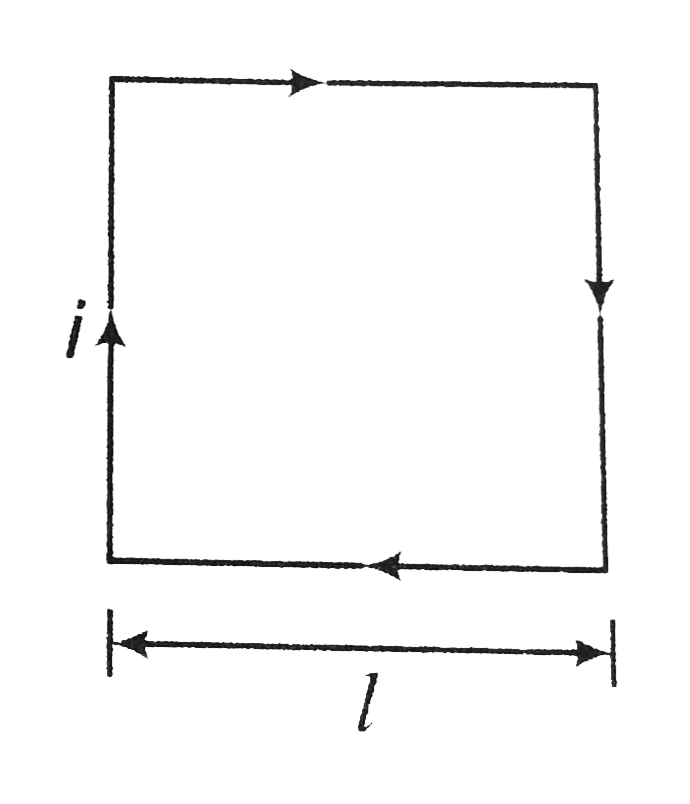
View Solutiona. A conductor in the shape of a square of edge length l=0.4m carries a current i=10.0A. Calculate the magnitude and direction of magnetic field at the centre of the square.
b. If this conductor is formed into a single circular turn and carries the same current. what is the value of the magnetic field at the centre.

View SolutionA current i is flowing in a straight conductor of length L. The magnetic induction at a point distant L4 from its centre will be-
View SolutionA cell is connected between two points of a uniformly thick circular conductor. The magnetic field at the centre of the loop will be
(Here i1 and i2 are the currents flowing in the two parts of the circular conductor of radius 'a' and μ0 has the usual meaning)
View SolutionA current i is flowing in a straight conductor of length L. The magnetic induction at a point distant L4 from its centre will be-
View Solution
