The diagram shows three cases. In all the three cases the circular part has radius r and straight ones are infinitely long . For the same current, i find ¯¯¯B at the centre P.

a) ¯¯¯Bp=μ0i4r⊙
b) ¯¯¯B2=BP=12μ0i2r⊗=μ0i4r⊗
c) ¯¯¯Bp=34μ0i2r⊗+μ0i4πr⊙=μ04ir(32−1π)⊗
Topper's Solved these Questions
- ELECTROMAGNETICSBOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETICSEXERCISE - ADDITIONAL EXERCISE
6 Videos
- ELECTROMAGNETICSBOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETICSEXERCISE - PROBLEMS (LEVEL -I)
30 Videos
- ELECTROMAGNETIC WAVESBOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - EXERCISE -II
20 Videos
- ELECTROSTATICSBOOK - AAKASH SERIESCHAPTER - ELECTROSTATICSEXERCISE - ADDITIONAL PRACTICE EXERCISE (PRACTICE SHEET (ADVANCED) INTEGER TYPE QUESTIONS)
4 Videos
Similar Questions
Knowledge Check
The magnetic field at the centre of a circular coil of radius r is π time that due to a long straight wire at a distance r from it for equal currents. The following figure show three cases. In all cases the circular part has radius r and straight ones are infinitely long. For same current, the B field at the centre P in cases 1, 2, 3, has the ratio
 A(−π2):(π2):(3π4−12)B(−π2+1):(π2+1):(3π4+12)C−π2:π2:3π4D(−π2−1):(π1−14):(3π4+12)
A(−π2):(π2):(3π4−12)B(−π2+1):(π2+1):(3π4+12)C−π2:π2:3π4D(−π2−1):(π1−14):(3π4+12)Figure shows three cases: in all case the circular part has radius r and straight ones are infinitely long. For the same current the ratio of field B at centre P in the three case B1:B2:B3 is
 A(−π2):(π2):(3π4−12)B(−π2+1):(π2+1):(3π4+12)C(−π2):(π2):(3π4)D(−π2−1):(π2−14):(3π4+12)
A(−π2):(π2):(3π4−12)B(−π2+1):(π2+1):(3π4+12)C(−π2):(π2):(3π4)D(−π2−1):(π2−14):(3π4+12)(Figure 3.139) shows three circular arcs, each of radius R and total charge as indicated. The net electric potential at the center of curvature.
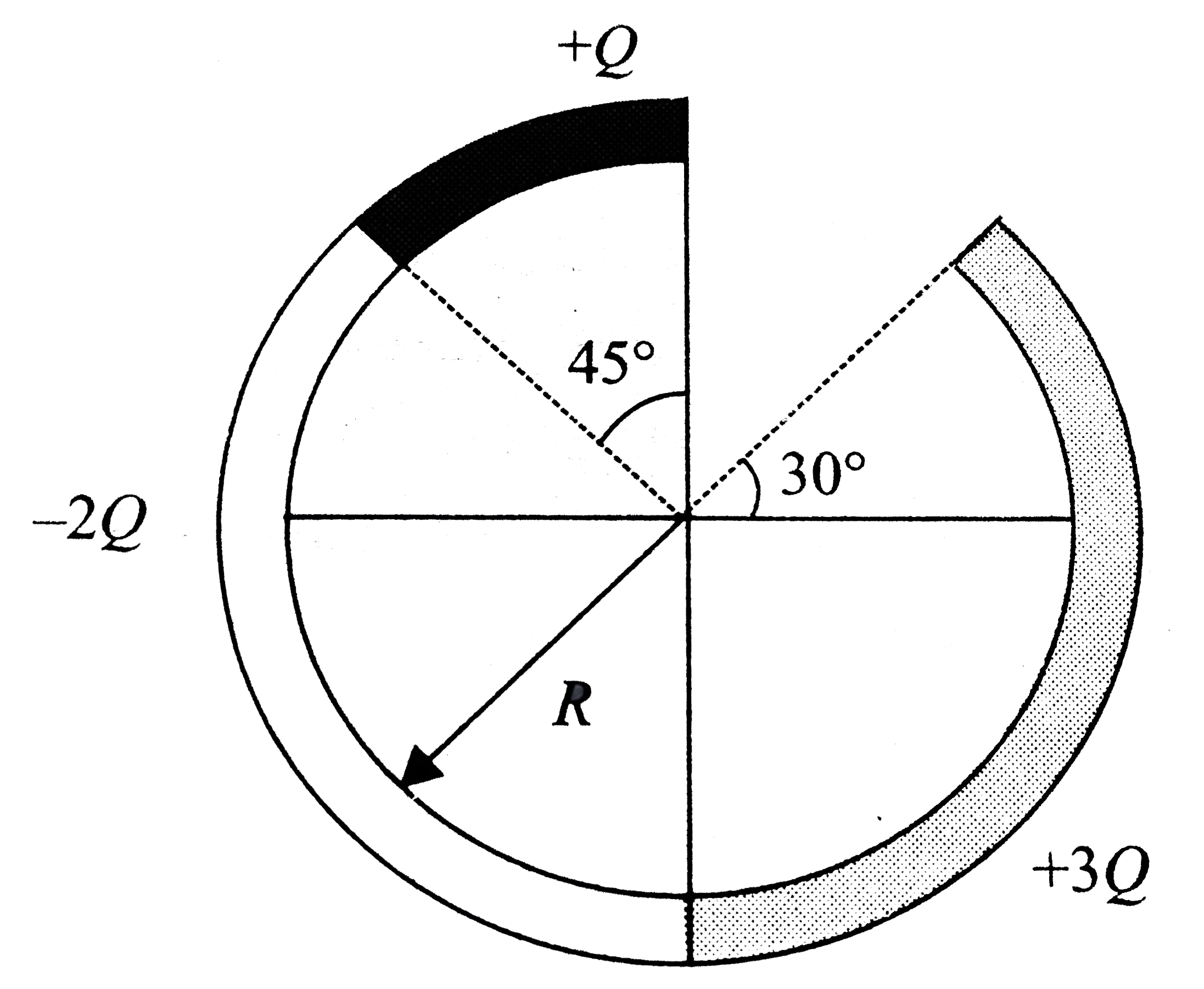 .AQ2πε0RBQ4πε0RC2Qπε0RDQπε0R
.AQ2πε0RBQ4πε0RC2Qπε0RDQπε0R
A circular coil 'A' has a radius R and the current flowing through it is I.Another circular coil 'B' has a radius 2R and if 21is the current flowing through it then the magnetic fields at the centre of the circular coil are in the ratio of
View SolutionA circular coil 'A' has a radius R and the current flowing through it is I.Another circular coil 'B' has a radius 2R and if 21is the current flowing through it then the magnetic fields at the centre of the circular coil are in the ratio of
View SolutionA circular coil 'A' has a radius R and the current flowing through it is I.Another circular coil 'B' has a radius 2R and if 2I is the current flowing through it then the magnetic fields at the centre of the circular coil are in the ratio of
View SolutionA circular coil carrying a current I has radius R and number of turns N. If all the three, i.e., the current I, radius R and number of turns N are doubled, then, magnetic, field at its centre becomes:
View Solution(Figure 3.139) shows three circular arcs, each of radius R and total charge as indicated. The net electric potential at the center of curvature.
 .
.
View Solution