Consider a non conducting plate of radius a and mass m which has a charge q distributed uniformly over it, The plate is rotated about its own axis with an angular speed $ω$ . Show that the magnetic moment M and the angular momentum L of the plate are related as $\frac{M}{L} = \frac{q}{2 m}$ .

Text Solution

Verified by Experts

$\frac{M}{L} = \frac{\frac{q ω a^{2}}{4}}{\frac{ω m a^{2}}{2}} = \frac{q}{2 m}$

|

Updated on:21/07/2023

Class 12 PHYSICS MOVING CHARGES AND MAGNETISM

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Consider a solid sphere of radius r and mass m which has a charge q distributed uniformly over its volume. The sphere is rotated about a diameter with an angular speed $ω$ . The magnetic moment of the sphere is
A $\frac{1}{3} q ω r^{2}$
B $\frac{1}{5} q ω r^{2}$
C $\frac{1}{7} q ω r^{2}$
D $\frac{1}{9} q ω r^{2}$
Question 2 - Select One
A thin disc of radius R has charge Q distributed uniformly on its surface. The disc is rotated about one of its diametric axis with angular velocity $ω$ . The magnetic moment of the arrangement is
A $\frac{Q R^{2} ω}{8}$
B $\frac{Q R^{2} ω}{4}$
C $\frac{Q R^{2} ω}{2}$
DZero
Question 3 - Select One
A disc of mass $m$ has a charge $Q$ distributed on its surface. It is rotating about an $X X'$ with a angular velocity $ω$ . The force acting on the disc is

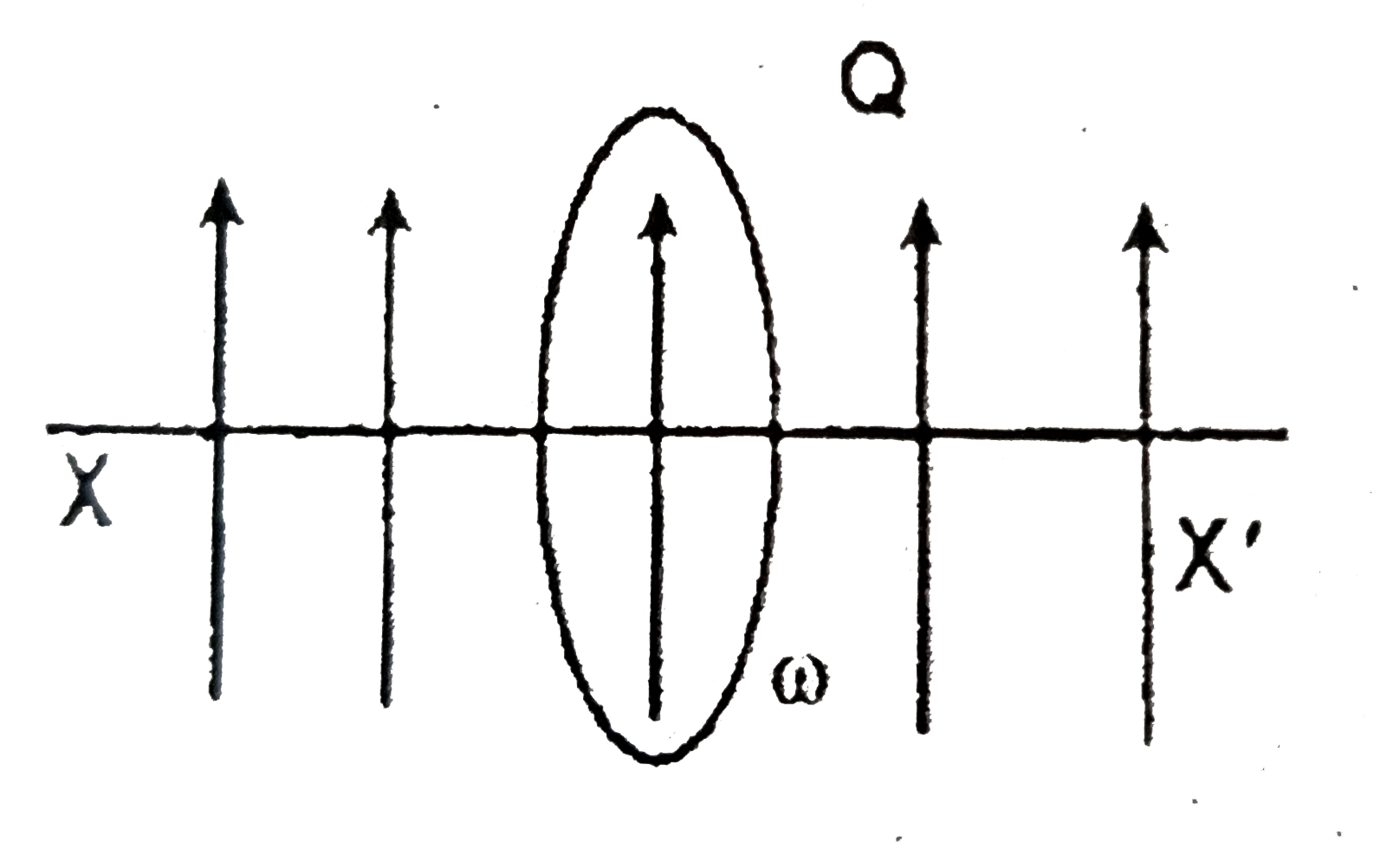Azero
B $ω R B / π$
C $2 Q ω B R$
Dnone of these

AAKASH SERIES-ELECTROMAGNETICS-PROBLEMS (LEVEL -II)

Home
Ask Doubt
Profile