Ring of radius R having uniformly distributed charge Q is mounted on a rod suspended by two identical strings as shown in fig. The tension in strings in equilibrium is T0. Now a vertical magnetic field is switched on and the ring is rotated at constant angular velocity Ω. Find the maximum Ω with which the ring can be rotated if the strings can withstand a maxiumum tension 3T02
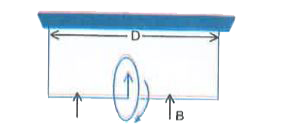
T0=ωQBR2Dorω=DT0QBR2
Topper's Solved these Questions
- ELECTROMAGNETICSBOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETICSEXERCISE - ADDITIONAL EXERCISE
6 Videos
- ELECTROMAGNETICSBOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETICSEXERCISE - PROBLEMS (LEVEL -I)
30 Videos
- ELECTROMAGNETIC WAVESBOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - EXERCISE -II
20 Videos
- ELECTROSTATICSBOOK - AAKASH SERIESCHAPTER - ELECTROSTATICSEXERCISE - ADDITIONAL PRACTICE EXERCISE (PRACTICE SHEET (ADVANCED) INTEGER TYPE QUESTIONS)
4 Videos
Similar Questions
A ring of radius R having unifromly distributed charge Q is mounted on a rod suspended by two identical strings. The tension in strings in equilibrium is T0. Now a vertical magnetic field is switched on and ring is rotated at constant angular velocity ω. Find the maximum ω with which the ring can be rotated if the strings can withstand a maximum tension of 3T0/2.

View SolutionA ring of radius R having unifromly distributed charge Q is mounted on a rod suspended by two identical strings. The tension in strings in equilibrium is T0. Now a vertical magnetic field is switched on and ring is rotated at constant angular velocity ω. Find the maximum ω with which the ring can be rotated if the strings can withstand a maximum tension of 3T0/2.

View Solution
Knowledge Check
A string has a linear mass density μ. The ends of the string are joined to form a closed loop and is given the shape of a circular ring of radius R. this ring is now rotated about its axis with an angular velocity ω
Q. The tension developed in the string isAμωR3B2μω2R2Cμω2R2Dμ2ω2R2
A ring of mass m and radius R is being rotated about its axis with constant angular velocity ω in the gravity free space. Find tension in the ring.
View SolutionA ring of radius R with a uniformly distributed charge q as shown in figure. A charge q0, is now placed at the centre of the ring. Find the increment in-the tension in ring.

View SolutionA conducting ring of radius r having charge q is rotating with angular velocity ω about its axes. Find the magnetic field at the centre of the ring.

View SolutionA conducting ring of radius r having charge q is rotating with angular velocity ω about its axes. Find the magnetic field at the centre of the ring.

View SolutionA conducting ring of radius r having charge q is rotating with angular velocity ω about its axes. Find the magnetic field at the centre of the ring.

View SolutionA charge Q is spread uniformly over an insulated ring of radius R.What is the magnetic moment of the ring if it is rotated with an angluar velocity ω about its axis?
View SolutionA string has a linear mass density μ. The ends of the string are joined to form a closed loop and is given the shape of a circular ring of radius R. this ring is now rotated about its axis with an angular velocity ω
Q. The tension developed in the string is
View Solution
