Let two cell of e.m.f's E1andE2 and internal resistances r1andr2 be connected in parallel to a circuit with an external resistance R. Find the value of the current I through the given resistor .

Electric cells connected in parallel to an external resistor. The current through the given resistor
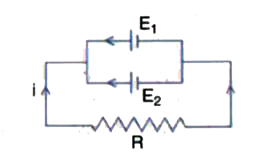
I=E1r1+E2r21+R[1r1+1r2]=E1r2+E2r1r1r21+R[r1+r2]r1r2
I=E1r2+E2r1r1r2+R[r1+r2]
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - AAKASH SERIESCHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE (LONG ANSWER QUESTIONS)
2 Videos
- CURRENT ELECTRICITYBOOK - AAKASH SERIESCHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE (SHORT ANSWER QUESTIONS)
1 Videos
- COMMUNICATION SYSTEMS BOOK - AAKASH SERIESCHAPTER - COMMUNICATION SYSTEMS EXERCISE - PRACTICE EXERCISE (TV Antenna)
16 Videos
- CURRENT ELECTRICITYBOOK - AAKASH SERIESCHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE - III
73 Videos
Similar Questions
Knowledge Check
n identical cells each of e.m.f. E and internal resistance r are connected in series. An external resistance R is connected in series to this combination. The current through R is
AnER+nrBnEnR+rCER+nrDnER+rA cell of e.m.f (E) and internal resistance (r) is connected in series with an external resistance (nr.) then the ratio of the terminal p.d. to E.M.F is
A1/nB1/(n+1)Cn/(n+1)D(n+1)/nA cell of e.mf. E and internal resistance r is connected in series with an external resistance nr. Then, the ratio of the terminal potential difference to E.M.F.is
A1/nB1n+1Cnn=1Dn+1n
Two batteries of e.m.f. E1 and E2 and internal resistance r1 and r2 are connected in parallel. Determine their equivelent e.m.f.
View SolutionA circuit consists of two cells, each of e.m.f. E and internal resistances r1 and r2 are connected in series through an external resistance X. If the potential difference between the ends of the first cell is zero, the value of X in terms of r1 and r2 will be
View Solutionn identical cells each of e.m.f. E and internal resistance r are connected in series. An external resistance R is connected in series to this combination. The current through R is
View SolutionA cell of e.mf. E and internal resistance r is connected in series with an external resistance nr. Then, the ratio of the terminal potential difference to E.M.F.is
View SolutionFour cells, each of emf E and internal resistance r, are connected in series across an external resistance reverse. Then, the current in the external circuit is
View Solution
