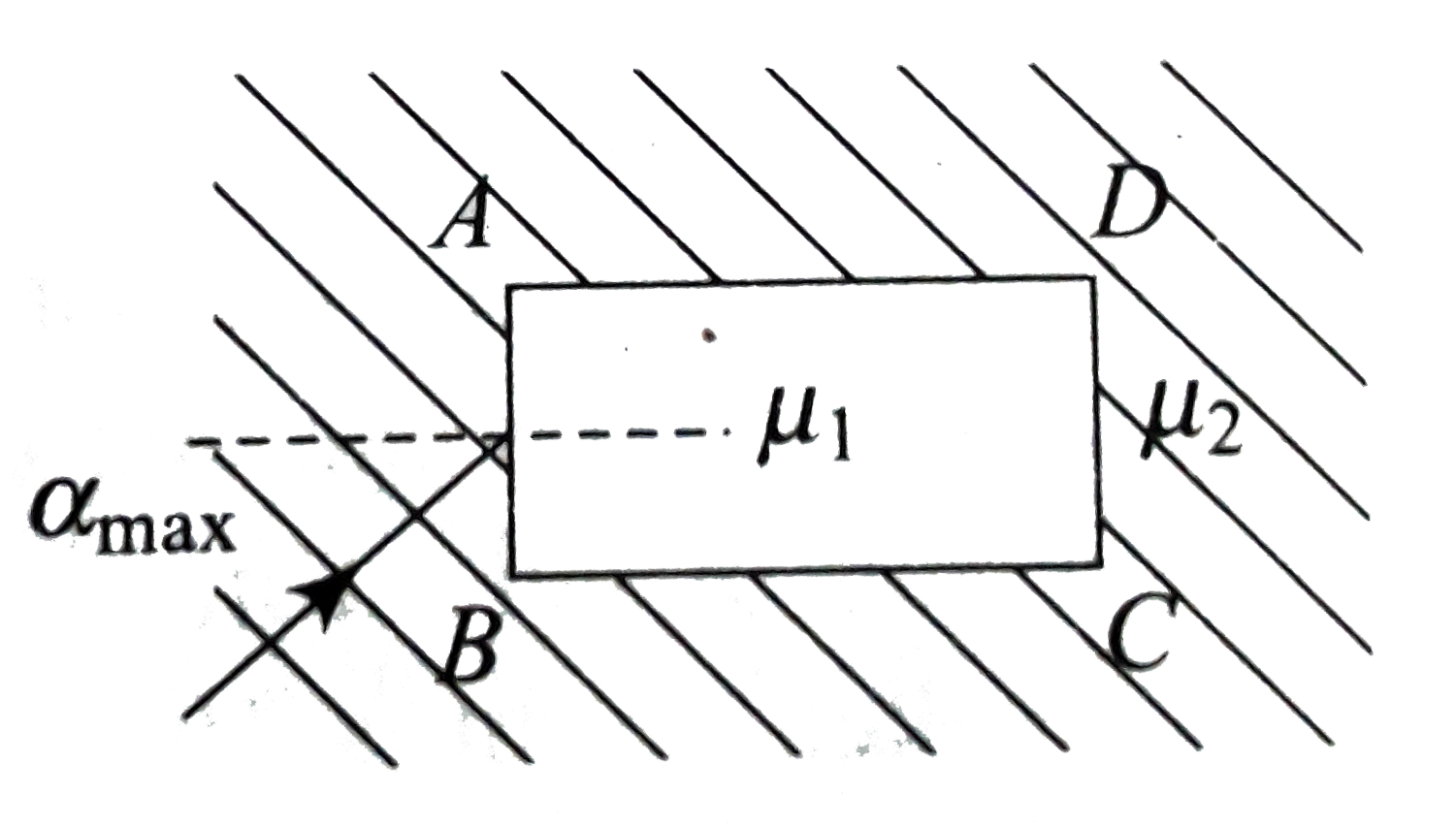
A rectangular glass slab ABCD of refractive index n1 is immersed in water of refractive index n2(n1>n2) A ray of light is incident at the surface AB of the slab as shown. The maximum value of the angle of incidence amax such that the ray comes out only from the other surface CD, is given by
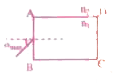
r1+r2=90∘,∴r1=90∘−r2
(r1)max=90∘−(r2)min
and(r2)min=θc
(for total internal reflection at AD)
where sinθc=n2n1orθc=sin−1(n2n1)
∴(r1)max=90∘−θc Now applying Snell.s law at face AB,
n1n2=sinamaxsin(r1)max=sinamaxsin(90∘−θc)=sinamaxcosθc
or sinamax=n1n2cosθc
∴amax=sin−1∣∣n1n2cosθc∣=sin−1[n1n2cos{sin−1(n2n1)}]

Topper's Solved these Questions
- RAY OPTICS BOOK - AAKASH SERIESCHAPTER - RAY OPTICS EXERCISE - EXERCISE I
95 Videos
- RAY OPTICS BOOK - AAKASH SERIESCHAPTER - RAY OPTICS EXERCISE - EXERCISE 1B
45 Videos
- PHYSICAL WORLDBOOK - AAKASH SERIESCHAPTER - PHYSICAL WORLDEXERCISE - VERY SHORT ANSWER TYPE QUESTIONS
5 Videos
- RIVISION EXERCISEBOOK - AAKASH SERIESCHAPTER - RIVISION EXERCISEEXERCISE - MOTION IN A PLANE (LAMNI.S THEOREM)
6 Videos
Similar Questions
A rectangular slab ABCD, of refractive index n1 , is immersed in water of refractive index n2(n1<n2). A ray of light is incident at the surface AB of the slab as shown in Fig. Find the maximum value of angle of incidence αmax, such that the ray comes out only from the other surface CD.
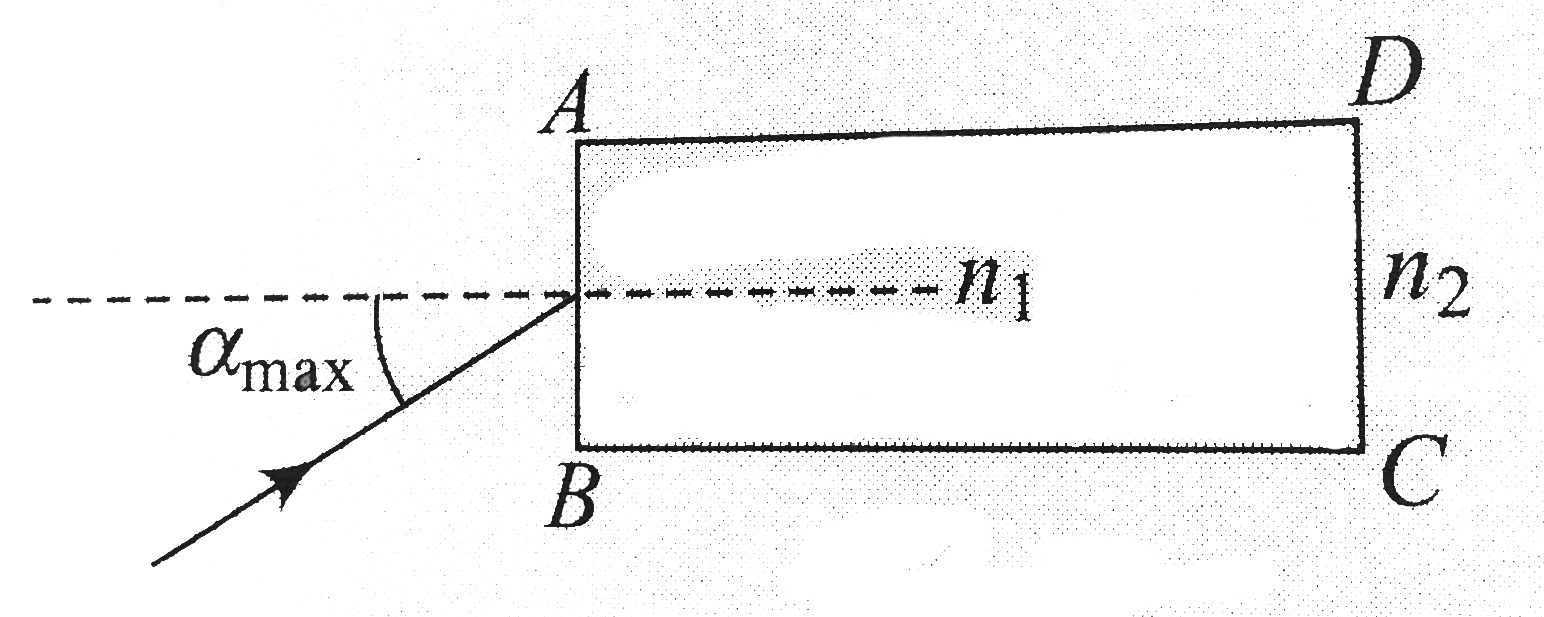
View SolutionA rectangular slab ABCD, of refractive index n1 , is immersed in water of refractive index n2(n1<n2). A ray of light is incident at the surface AB of the slab as shown in Fig. Find the maximum value of angle of incidence αmax, such that the ray comes out only from the other surface CD.
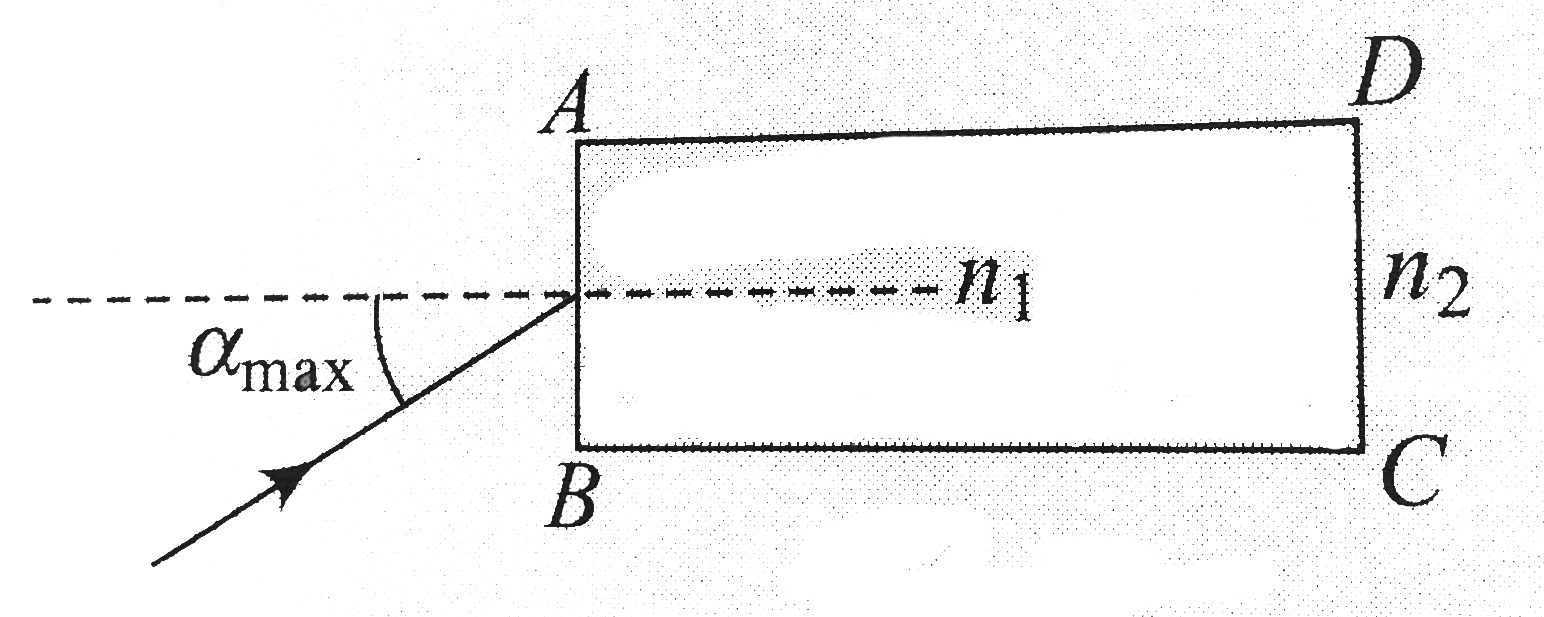
View Solution
Knowledge Check
A rectengular glass slab ABCD of refractive index n_1 is immersed in water of refractive index n2(n1>n2). A ray of light is incident at the surface AB of the slab as shown. The maximum value of the angle of incidence αmax such that the ray comes out only from the other surface CD is given by
 Asin−1[n1n2cos(sin−1(n2n2))]Bsin−1[n1cos(sin−1(1n2))]Csin−1(n1n2)Dsin^-1((n_2)/(n_2))
Asin−1[n1n2cos(sin−1(n2n2))]Bsin−1[n1cos(sin−1(1n2))]Csin−1(n1n2)Dsin^-1((n_2)/(n_2))A rectangular glass slab ABCD of refractive index n1 is immersed in water of refractive index n2(n1<n2). A ray of light is incident at the surface AB of the slab as shwon. The maximum value of the angle of incidence αmax such that the ray comes out from the other surface CD is given by
 Asin−1[n1n2cos(sin−1(n2n1))]Bsin−1[n1cos(sin−1(1n2))]Csin−1(n1n2)Dsin−1(n2n1)
Asin−1[n1n2cos(sin−1(n2n1))]Bsin−1[n1cos(sin−1(1n2))]Csin−1(n1n2)Dsin−1(n2n1)A rectangular glass slab ABCD, of refractive index n1, is immersed in water of refractive index n2(n1>n2). A ray of light in incident at the surface AB of the slab as shown. The maximum value of the angle of incidence αmax, such that the ray comes out only from the other surface CD is given by
Asin−1[n1n2cos(sin−(1)n2n1)]Bsin−1[n1cos(sin−11n2)]Csin−1(n1n2)Dsin−1(n2n1)
A glass slab made of a material of refractive index n1 is kept in a medium of refractive index n2.
A light ray is incident on the slab. Draw the path of the rays of light emerging from the glass slab, if n1>n2
View SolutionA glass slab made of a material of refractive index n1 is kept in a medium of refractive index n2.
A light ray is incident on the slab. Draw the path of the rays of light emerging from the glass slab, if n1=n2
View SolutionA glass slab made of a material of refractive index n1 is kept in a medium of refractive index n2.
A light ray is incident on the slab. Draw the path of the rays of light emerging from the glass slab, if n1<n2
View SolutionA cubical block of glass of refractive index n1 is in contact with the surface of water of refractive index n2. A beam of light is incident on vertical face of the block. After refraction a total internal reflection at the base and refraction at the opposite face take place. The ray emerges at angle θ as shown. The value of θ is given by

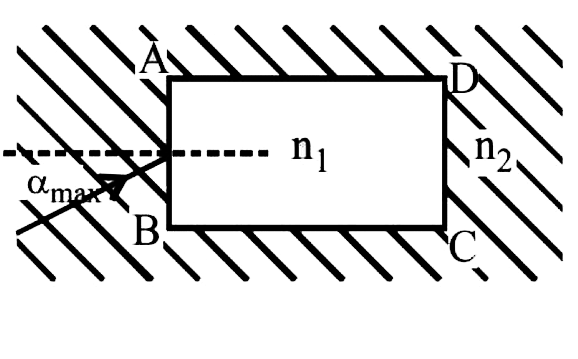
View SolutionA rectangular glass slab ABCD of refractive index n1 is immerged in water of refractive index n2(n1>n2) . A ray of light is incident at the surface AB of the slab as shown . The maximum value of the angle of incidence αmax , such that the ray comes out only from the other surface CD , is given by :-
_E01_205_Q01.png)
View Solution
