Question

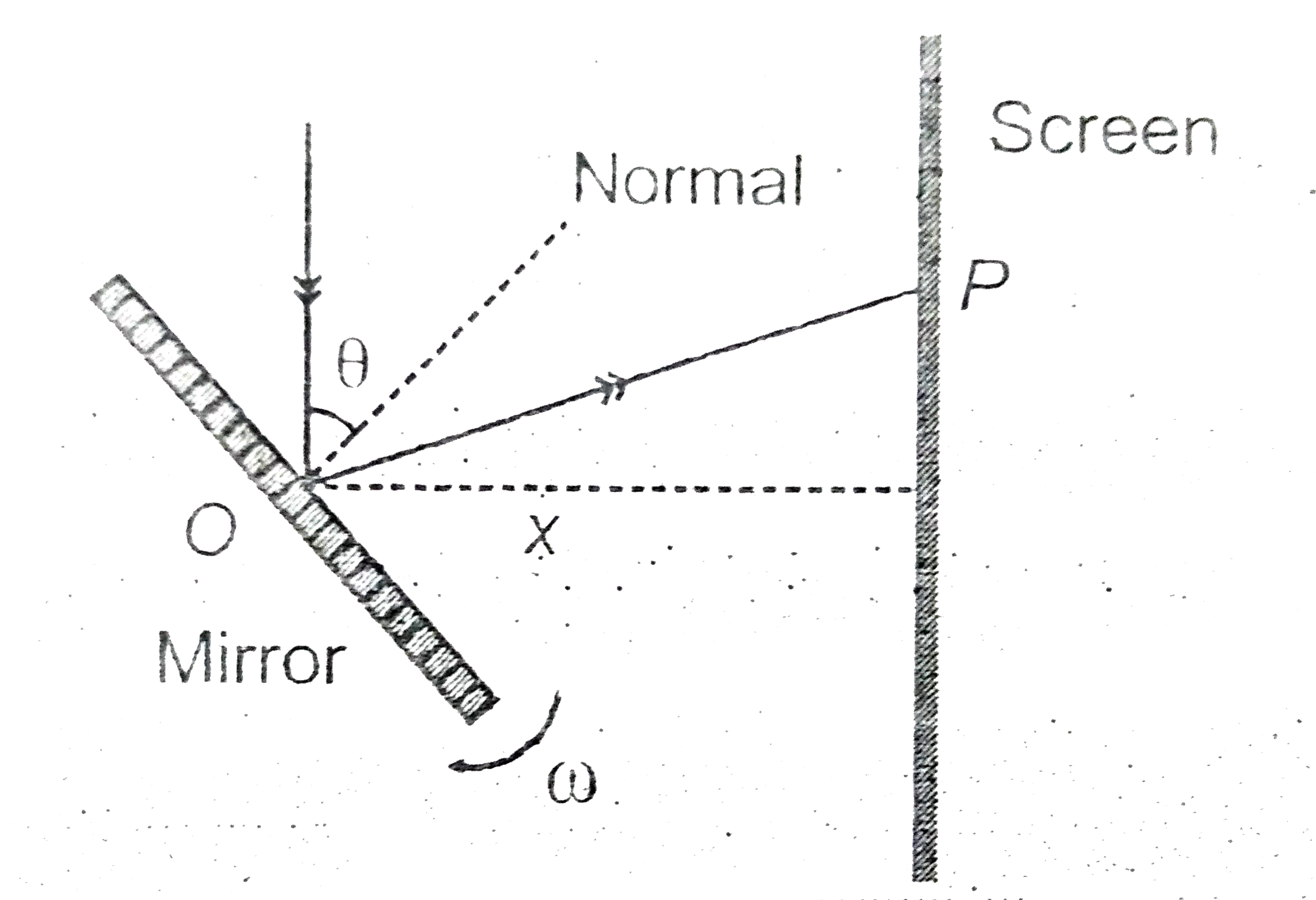
Figure shows a plane mirror hinged at O and free to rotate in a vertical plane. The point O is at a distance x from a long screen. A beam of light moving vertically downwards is reflected by the mirror at O so that a bright spot P is formed at the screen. At the instant shown, the angle of incidence is $\theta$ and the mirror is rotating clockwise with constant angular veloity $\omega$. Find the speed of spot P at this instant.

Explanation

Various angles are shown in the figure.

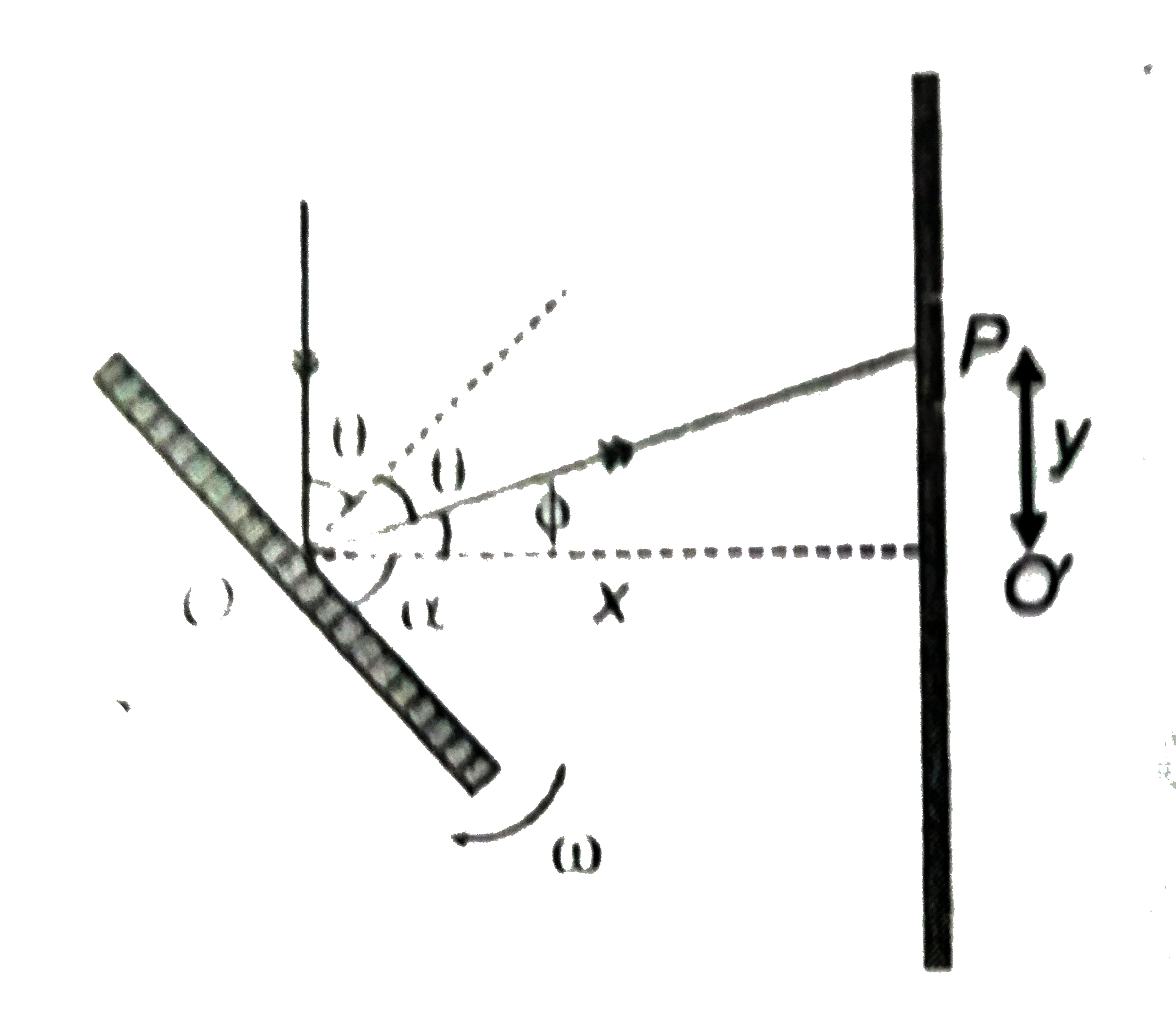
The distance of point P from O' is y at this instant.
You are supposed to calculate `(dy)/(dt)`.
From the figure,
`theta + theta +phi = 90^(@)` ....(i)
`theta + phi + alpha = 90^(@)` ...(ii)
`rArr alpha = theta`
`rArr phi = 2theta = 90^(@)`
or `phi + 2alpha = 90^(@)`
`(d phi)/(dt) + 2(d alpha)/(dt) = 0`
`rArr (d phi)/(dt) = -2(d alpha)/(dt)`
Note : This shows that angular speed of reflected ray is double that of mirror.
Now, `y = x tan phi`
`rArr (dy)/(dt) = x sec^(2) varphi (d varphi)/(dt)`
`rArr (dy)/(dt) = -x sec^(2) varphi xx 2omega`
Speed `= |(dy)/(dt)| = +2x (sec^(2) phi)omega`