The guage pressure exerted below a column of water, open to the earth's atmosphere at depth of 10 m is (density of water = 1000 kg/m3, g = 10 m/s2 and 1 atm pressure = 105 Pa)
1 atm
2 atm
3 atm
4 atm
The correct Answer is:A
To find the gauge pressure exerted below a column of water at a depth of 10 meters, we can use the formula for pressure in a fluid column, which is given by:
P=ρgh
Where:
- P is the gauge pressure,
- ρ is the density of the fluid (water in this case),
- g is the acceleration due to gravity,
- h is the height (or depth) of the fluid column.
Step 1: Identify the given values
- Density of water, ρ=1000kg/m3
- Acceleration due to gravity, g=10m/s2
- Depth of water column, h=10m
Step 2: Substitute the values into the formula
Now, substitute the values into the pressure formula:
P=ρgh=(1000kg/m3)×(10m/s2)×(10m)
Step 3: Perform the multiplication
Calculating the above expression:
P=1000×10×10=100000Pa
Step 4: Convert the pressure to standard units
The pressure we calculated is in Pascals (Pa). Since 1Pa=1N/m2, we can express this as:
P=105Pa
Step 5: Relate to atmospheric pressure
We know that 1atm=105Pa. Therefore, we can conclude:
P=1atm
Final Answer
The gauge pressure exerted below the column of water at a depth of 10 meters is 1atm.
---
- P is the gauge pressure,
- ρ is the density of the fluid (water in this case),
- g is the acceleration due to gravity,
- h is the height (or depth) of the fluid column.
- Density of water, ρ=1000kg/m3
- Acceleration due to gravity, g=10m/s2
- Depth of water column, h=10m
Now, substitute the values into the pressure formula:
Calculating the above expression:
The pressure we calculated is in Pascals (Pa). Since 1Pa=1N/m2, we can express this as:
We know that 1atm=105Pa. Therefore, we can conclude:
The gauge pressure exerted below the column of water at a depth of 10 meters is 1atm.
Topper's Solved these Questions
Similar Questions
Find the pressure exerted below a column of water, open to the atmosphere, at depth
(i) 10 m " " (ii) 30 m
(Given, density of water =1×103kgm−3,g=10ms−2)
View SolutionFind the pressure exerted below a column of water, open to the atmosphere, at depth
(i) 5 m
(ii) 20 m
(Given, density of water = 1×103kg m−3,g=10ms−2)
View Solution
Knowledge Check
The pressure at a point in water is 10 N/m2. The depth below this point where the pressure becomes double is (Given density of water = 103 kg m−3, g = 10 m s−2)
A1 mmB1 cmC1 mD10 cmAt what depth in fresh water the pressure on a diver is one atmosphere ?
[Density of water =103kgm−3, Normal pressure =105Pa,g=10ms−2]A11 mB10.5 mC10 mD9.8 mAt a depth of 500 m in an ocean what is the absolute pressure? Given that the density of seawater is 1.03×103kgm−3 and g=10ms2
A40 atmB52 atmC32 atmD62 atm
Calculate the pressure at a depth of 10 m in an Ocean. The density of sea water is 1030kg/m3. The atmospheric pressure is 1.01×105 pa.
View SolutionCalculate the total pressure at the bottom of a lake of depth 5.1 m (atm pressure =105 P), density of water =103kg/m3,g=10m/s2
View SolutionA glass full of water has a bottom of area 20cm2, top of area 20cm, height 20cm and volume half a litre.
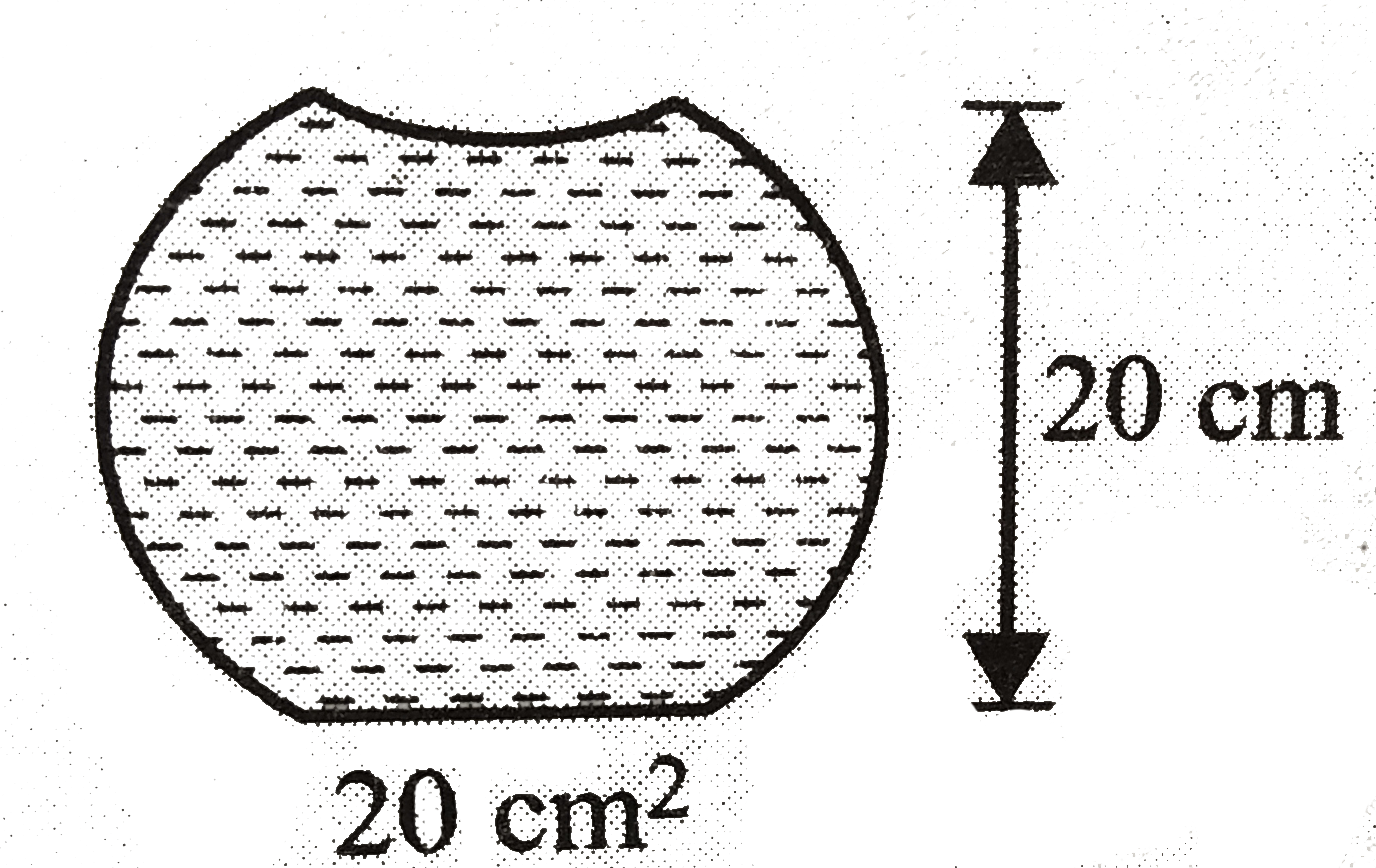
a. Find the force exerted by the water on the bottom.
b. Considering the equilibrium of the v, after. find the resultant force exerted by the side, of the glass on the water. Atmospheric pressure =1.0×105N/m2. Density of water =1000kg/m−3 and g=10m/s2
View SolutionA vessel full of water has a bottom of area 20cm2, top of area 20cm2, height 20 cm and volume half a litre as shown in figure.
(a) find the force exerted by the water on the bottom.

(b) considering the equilibrium of the water, find the resultant force exerted by the sides of the glass vessel on the water. atmospheric pressure =1.0×105N/m2. density of water =1000kg/m3 and g=10m/s2
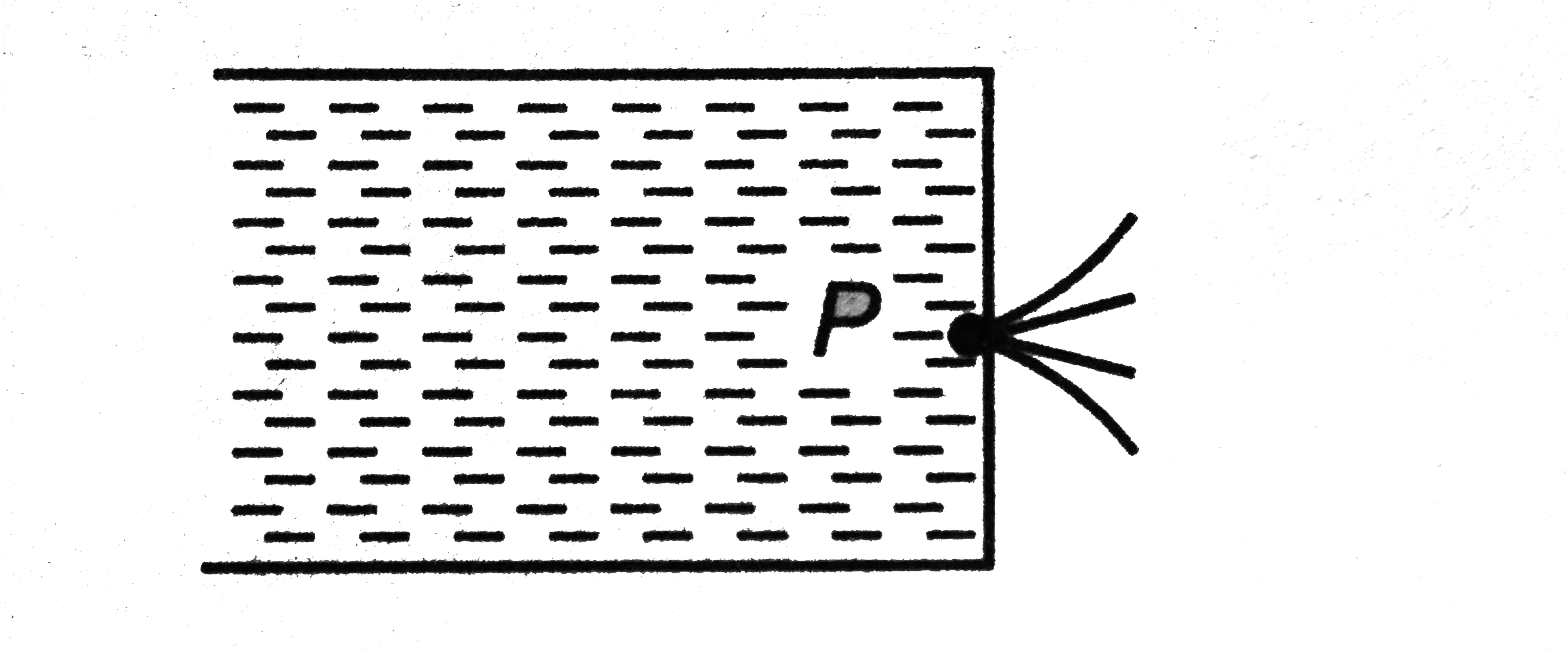
View SolutionA leakage begins in water tank at position P as shown in the figure. The gauge pressure (pressure above that of the atmosphere) at P was 5×105N/m2. If the density of water is 1000kg/m3 the initial velocity with which water gushes out is approximately
View Solution
