In the figure given below, find the
(a) equivalent capacitance of the network between points A and B.
Given: C1=C5=8μF,C2=C3=C4=4μF.
(b) maximum charge supplied by the battery, and
(c ) total energy stored in the network.
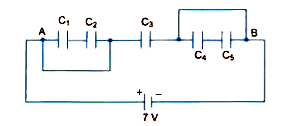
(a) In the network capacitors C1andC2 as well as C4andC5 are short circuited and do not contribute to equivalent capacitance of the circuit.
∴ Equivalent capacitance C=C3=4μF.
(b) ∴ Charge supplied by the battery Q=CV=(4μF)×7V=28μC
(c ) Total energy stored in the network U=12CV2=12(4F)×(7V)2=98μJ
Topper's Solved these Questions
- CBSE EXAMINATION PAPER 2020 BOOK - U-LIKE SERIESCHAPTER - CBSE EXAMINATION PAPER 2020 EXERCISE - SECTION D
12 Videos
- CBSE EXAMINATION PAPER 2020 BOOK - U-LIKE SERIESCHAPTER - CBSE EXAMINATION PAPER 2020 EXERCISE - SECTION B
1 Videos
- ATOMSBOOK - U-LIKE SERIESCHAPTER - ATOMSEXERCISE - SELF ASSESSMENT TEST (SECTION C)
2 Videos
- CBSE EXAMINATION PAPER 2020 (SOLVED)BOOK - U-LIKE SERIESCHAPTER - CBSE EXAMINATION PAPER 2020 (SOLVED)EXERCISE - SECTION D
11 Videos
Similar Questions
In the figure given below, find the, (a) equivalent capacitance of the network between points A and B. Given: C1=C5=4μF, C2=C3=C4=2μF (b) maximum charge supplied by the battery, and (c) total energy stored in the network

View SolutionIn the figure given below, find the, (a) equivalent capacitance of the network between points A and B. Given: C1=C5=4μF, C2=C3=C4=2μF (b) maximum charge supplied by the battery, and (c) total energy stored in the network

View Solution
Knowledge Check
The equivalent capacitance of the network given below is 1μF. The value of 'C' is.
 .A3μFB1.5μFC2.5μFD1μF
.A3μFB1.5μFC2.5μFD1μF
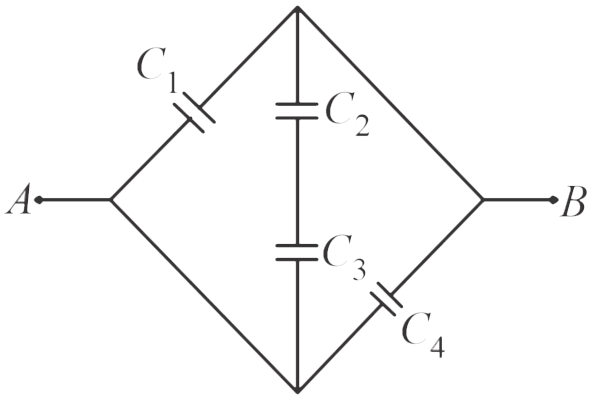
In a given network the equivalent capacitance between A and B is [C1=C4=1μF,C02=C3=2μF]
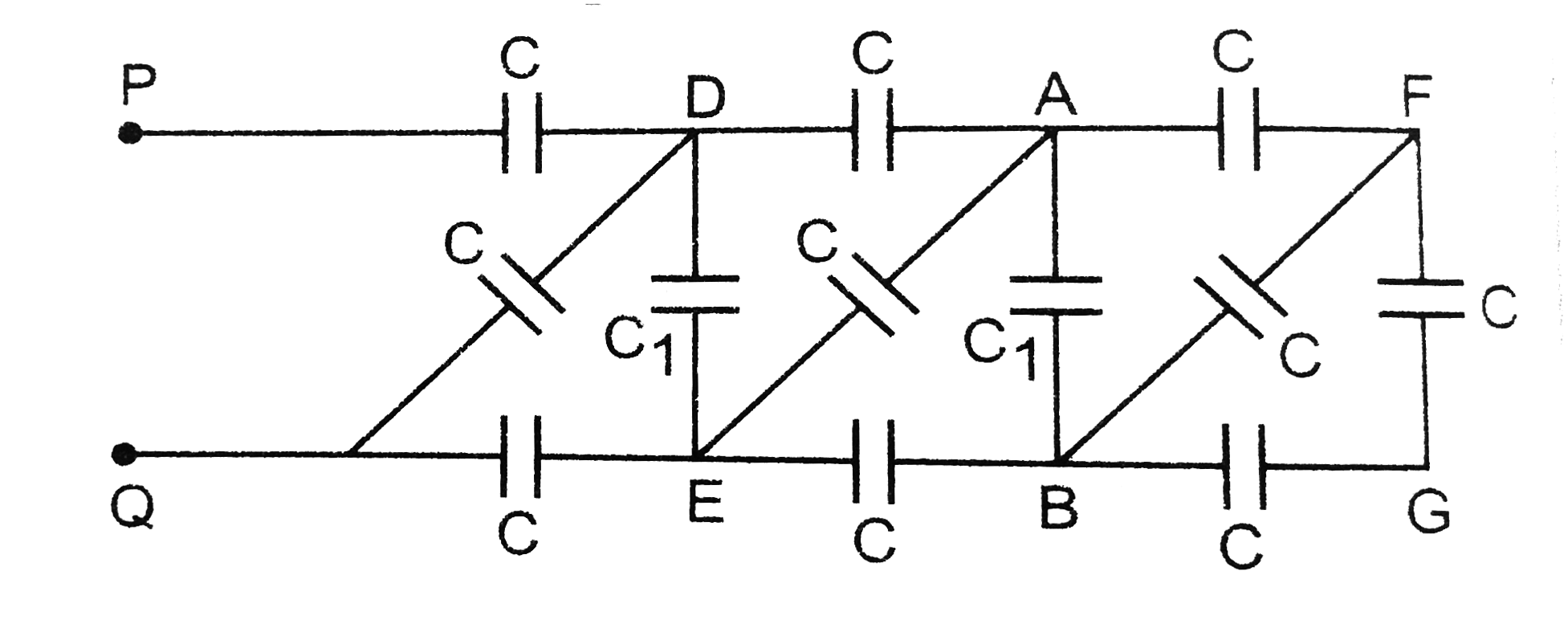
View SolutionFind the equivalent capacitane between the points P and Q as shown in Fig. Given C=18μF and C1=12μF
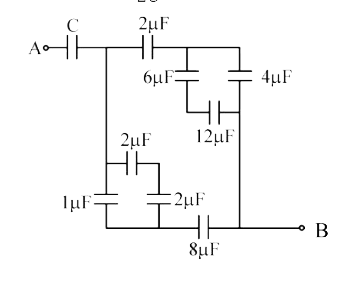
View SolutionIn the given network, the value of C, so that an equivalent capacitance between A and B is 3uF
View SolutionThe equivalent capacity between A and B in the given circuit is (C1=4μF,C2=12μF,C3=8μF,C4=4μF,C5=8μF)

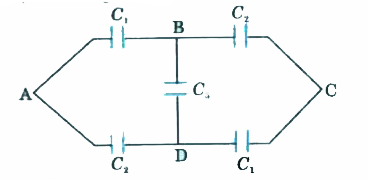
View SolutionConsider the network of capacitors as shown in the figure. Find equivalent capacitance between points A and C. Assume C1=1μF,C2=0.5μFandC3=1μF.
View SolutionIn the network of capacitors given ahead. Find the effective capacitance between point P and Q
If C1=C2=C3=C4=4μF
Value is not given C1andC2

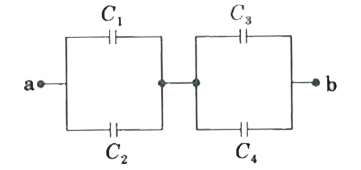
View SolutionCalculate the effective capacitance between a and b from the figure given below:
C1=C3=100μF,C2=C4=200μF.
View Solution
